Lecture Notes 27: More Computational Complexity ( P and NP)

Outline

This class we’ll discuss:

P and NP

A Slideshow:

GUIDED NOTES (Optional)

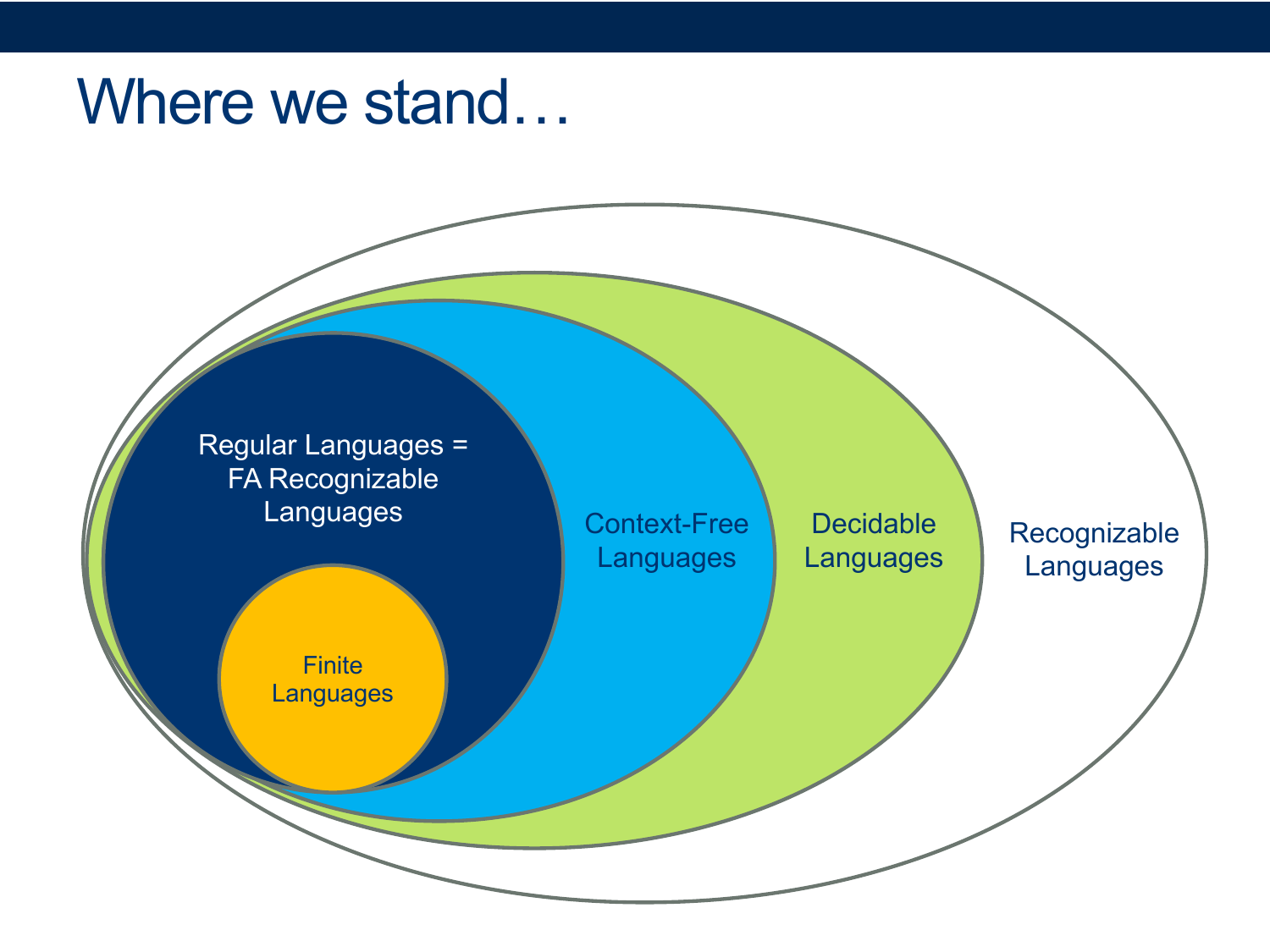
Recap: Computational Complexity

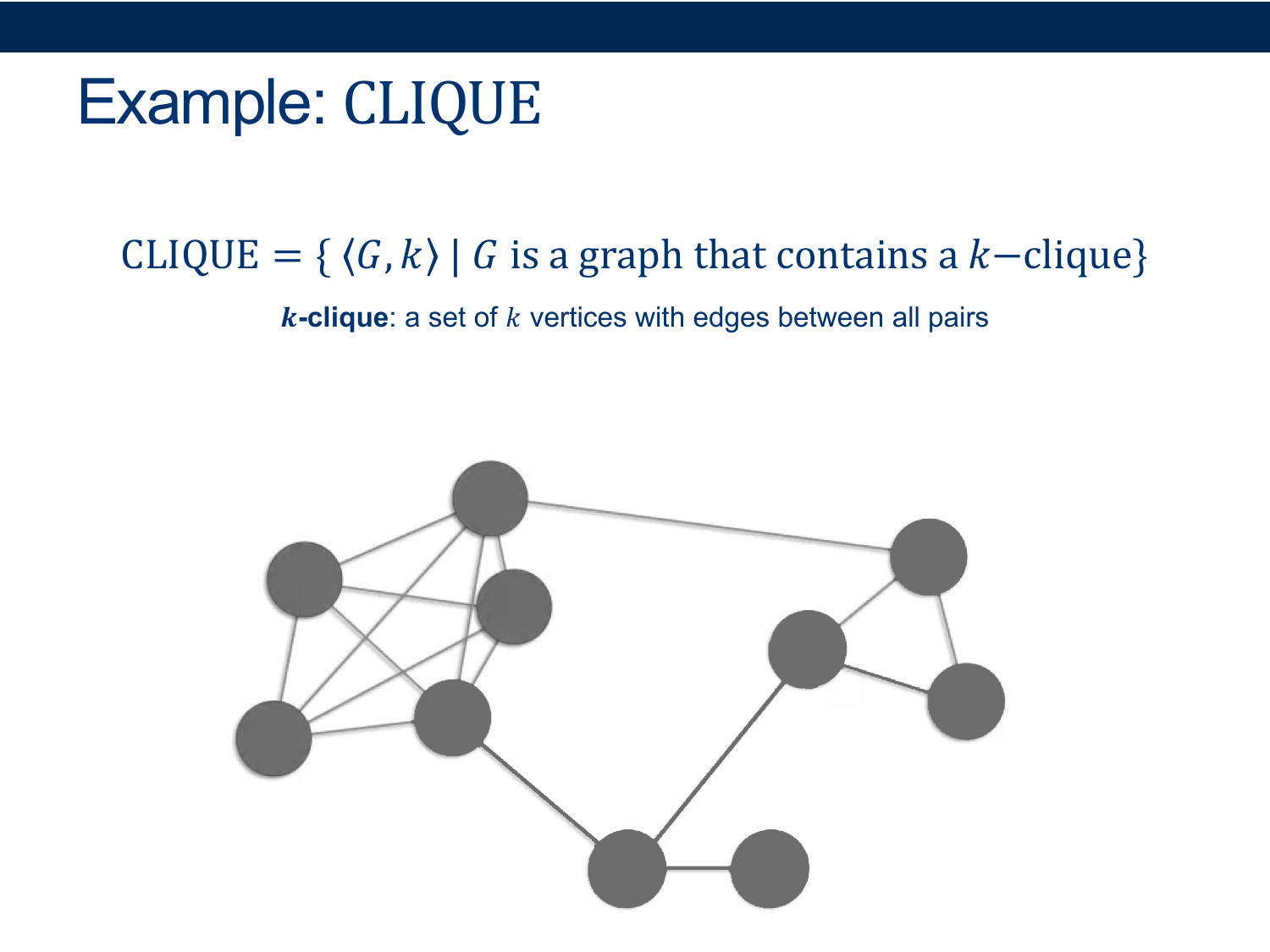
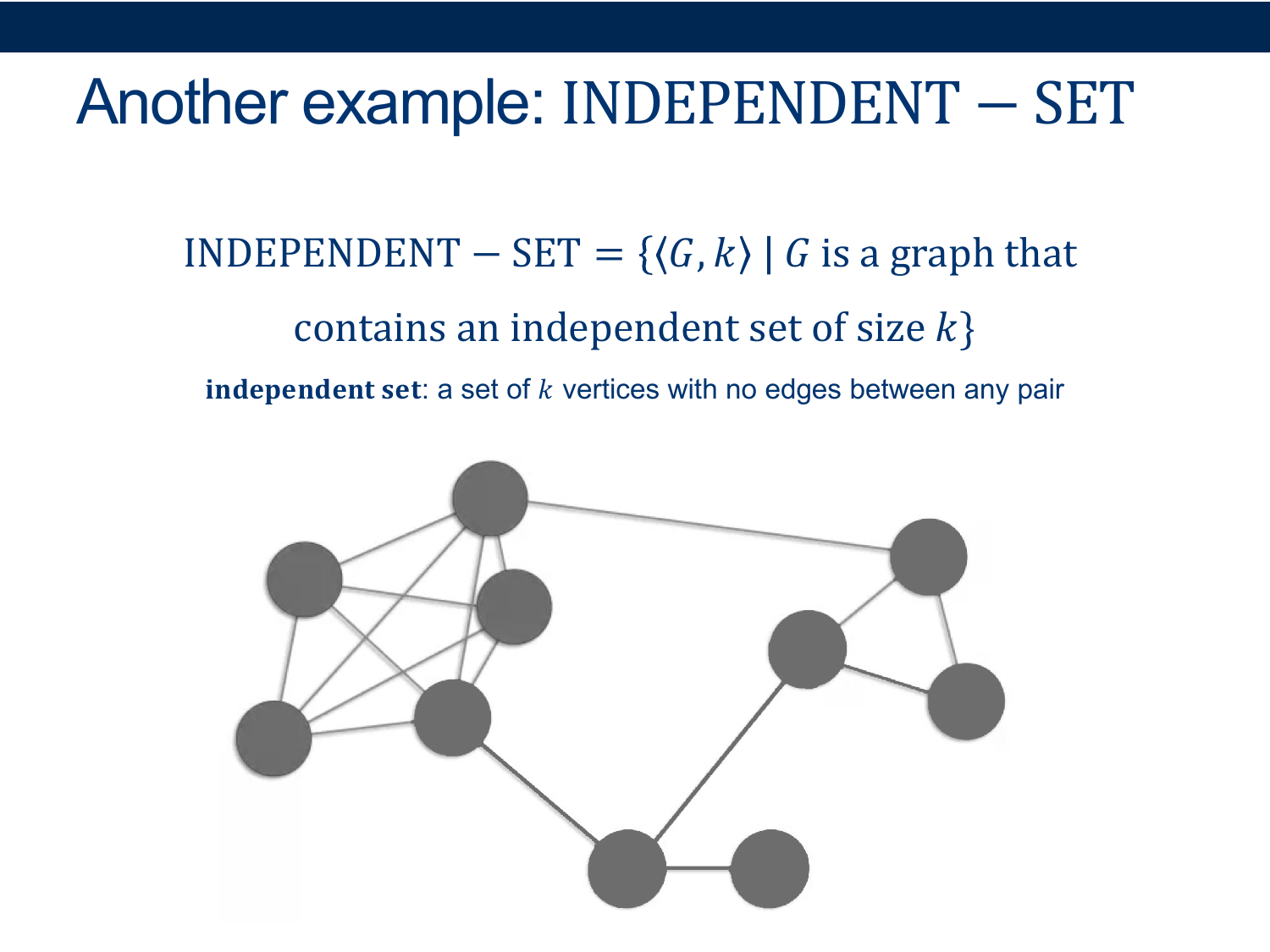
Activity 1 [2 minutes] How would you Prove this?:

answer:

(Wait; then Click)

To show a language is in NP using a verifier:

Specify a certificate that can be used with a verifier to decide the language.
Give a verifier that uses that certificate to verify membership in the given language.
Prove that the language recognized by the verifier is the given language and that the verifier runs in polynomial time.

Certificate: a graph and a set of k vertices we claim is a cliquebr Verifier: loop over all pairs in the set and check to make sure there’s an edge between them, and if so: ACCEPT - O(k^2) (can’t be bigger than n^2)

Activity 2 [2 minutes] How would you Prove this?:

answer:

(Wait; then Click)

Nondeterminism: we can try multiple “branches” of computation at once The trick: each branch can only take polynomial time Nondeterministically test all subsets of vertices. On each subset: loop over all pairs in the (sub)set and check to make sure there’s an edge between them, and if so: ACCEPT - O(n^2) if no branch accepts REJECT Guaranteed to halt? YES (there’s nowhere to get stuck) What would happen if we tried to serialize all the branches?

how many possible subsets do we have to check? $2^n$ <-- not polynomial anymore
note: this just means that this particular algorithm doesn’t run in polynomial time, but it turns out we haven’t been able to find any polynomial-time deciders for this language