Lecture Notes 23: Rice’s Theorem
Outline
This class we’ll discuss:
- Rice’s Theorem
A Slideshow:
GUIDED NOTES (Optional)
Rice’s Theorem

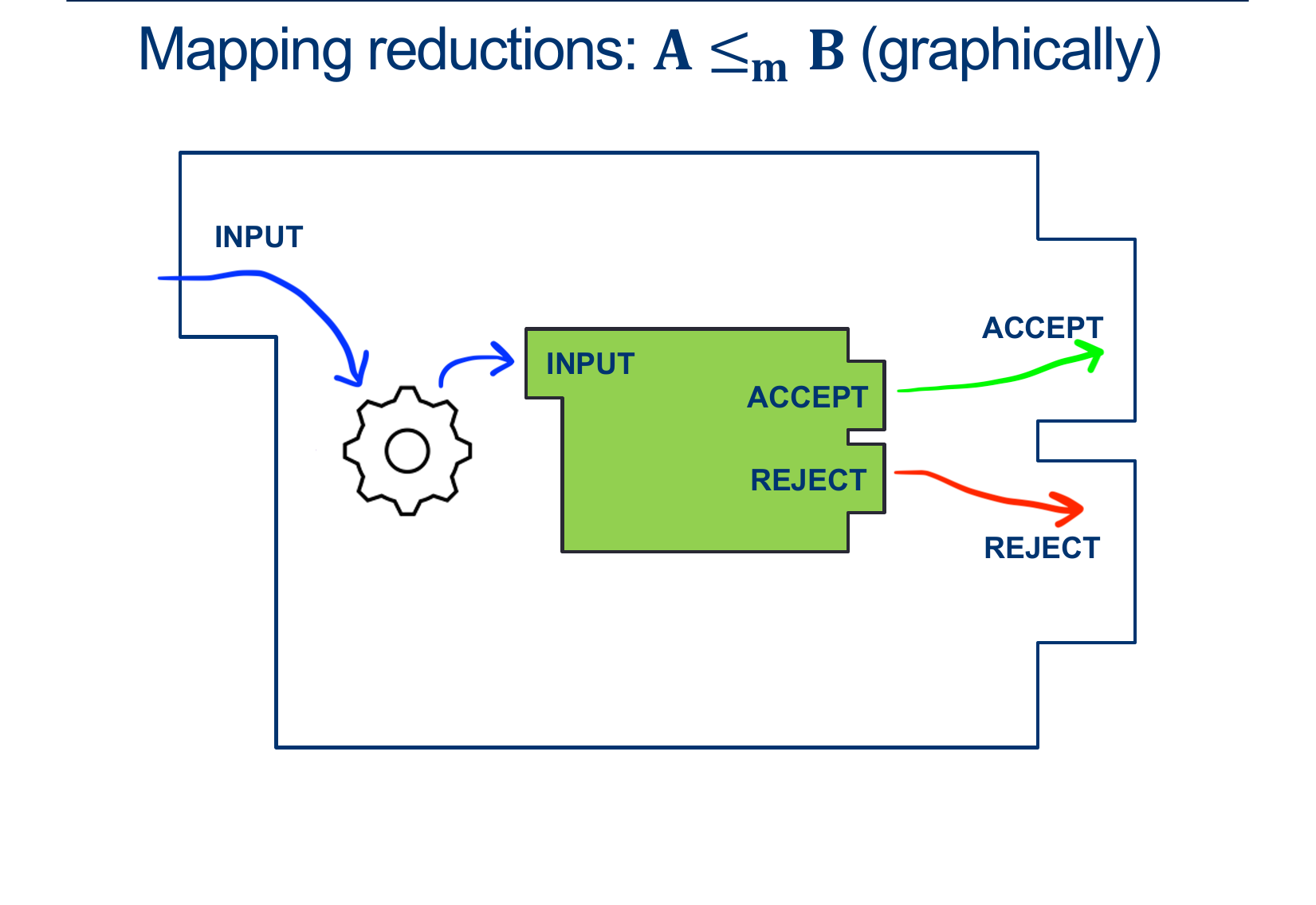
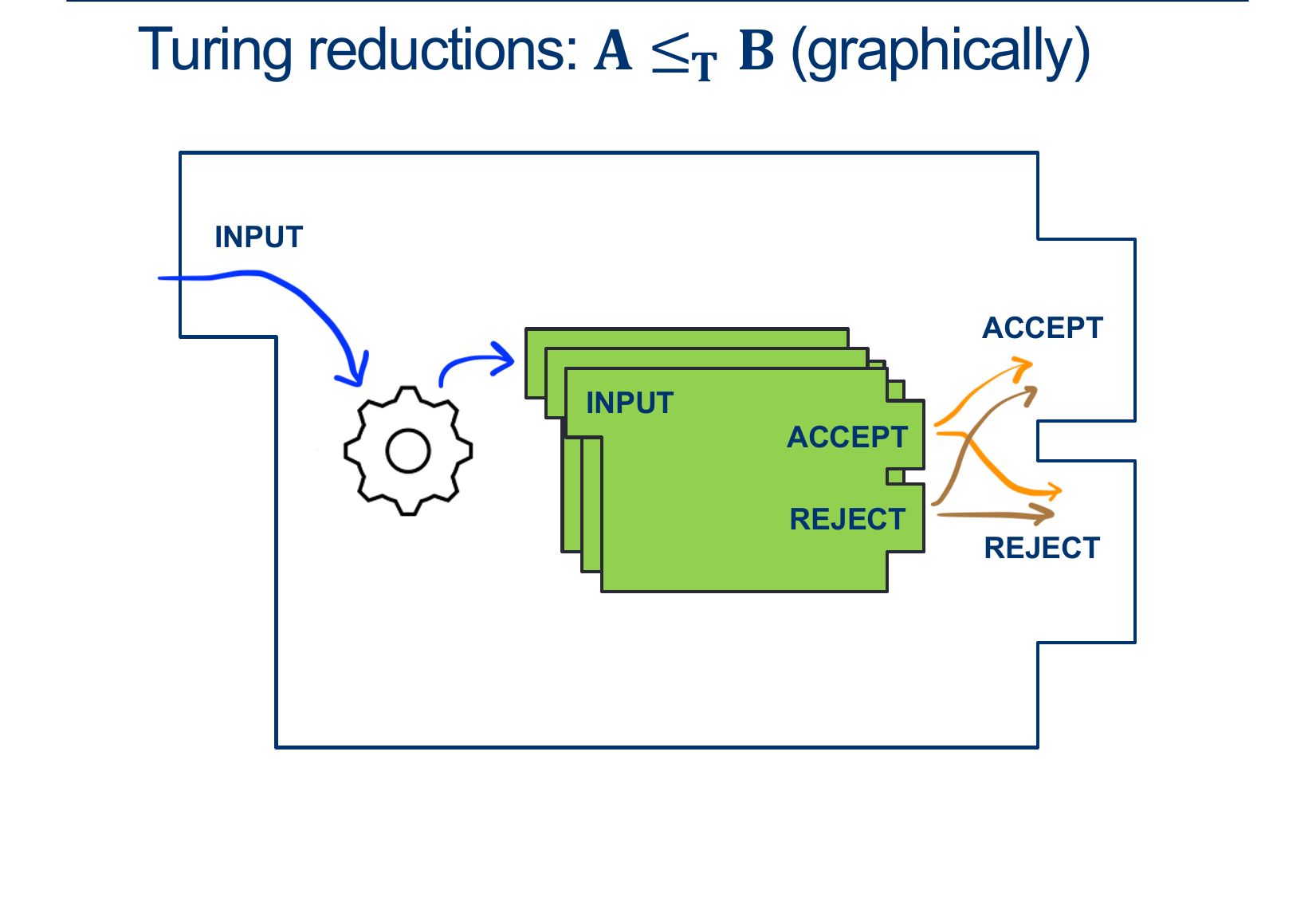

Our previous example:










Remember, we have to be able to deal with any input, but we don’t necessarily have to map them all to unique outputs.
This is why a mapping reduction is sometimes called a “many-one” reduction.

Let’s start by assuming that ∅ ∉ P (that is, it doesn’t exhibit the non-trivial property we care about).
Because we’re trying to prove undecidability, I claim that we can assume this WLOG.
Why? (otherwise, just work with the complement of P).
Let M1 be any TM such that L(M1) = ∅, so < M1 > ∉ MP.
Cool, so now we’ve got something we could map not-in-ATM words to.

Next let M2 be any TM such that L(M2) ∈ P, so < M1 > ∈ MP.
How do we know M2 exists?
Because P is nontrivial.
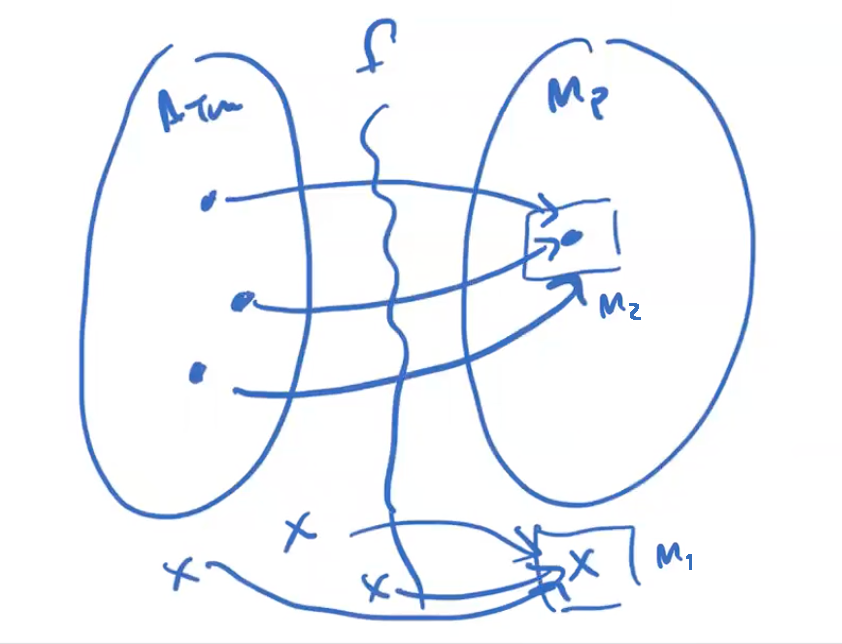

We have M1 not in P, M2 in P
\[\begin{align*} \text{Goal:}&\\ \quad & \text{On any input x: }\\ \quad & \quad \text{if } x = < M,w >\in ATM \text{, map to something in MP}\\ \quad & \quad \text{otherwise, map to something not in MP (like M1)}\\ \end{align*}\]Easy part: If x isn’t of the form $< M,w >$ return something $\notin$ MP, like $< M1 >$.
Harder part: If x IS of the form $< M,w >$ , we have two cases: if it’s in ATM, we want to map it to a machine in MP and if it’s NOT in ATM, we want to map it to something not in MP.

Time to get tricksy: if x is of the form $< M,w >$ , then return the following machine: $< M^{\prime}_{M,w} >$
\(\begin{align*} <M^{\prime}_{M,w}>:&\\ \quad & \text{On any input y: }\\ \quad & \quad \text{Run M on w. #(If stuck on a loop, this is M1!)}\\ \quad & \quad \quad \text{If M accepts w then run M2 on y ADWID}\\ \quad & \quad \quad \text{If M rejects w, REJECT.}\\ \end{align*}\)
If M accepts w, what is $<M^{\prime}_{M,w}>$’s language?
exactly the same as M2’s, which means this machine is in MP
(If M accepts w, then $< M^{\prime}_{M,w} >$ is just the result of M2)
If M doesn’t accept w, what is its language?
the empty language, exactly like M1, which means NOT in MP
(If M doesn’t accept w,$< M^{\prime}_{M,w} >$ is just M1)
Therefore, ATM $\leq_m$ MP using this process.
This implies that MP is undecidable




