Lecture Notes 12: Intro to Push-Down Automata
Outline
This class we’ll discuss:
- More on CFGs
- Intro to Push-Down Automata
A Slideshow:
GUIDED NOTES (Optional)
Recap: CFGs

All REs can be created with CFGs
Approach 1: Recursive creation of CFG from definition of REs
For any RE $R_1$ We can produce a CFG $G_1$ by applying the following steps:
- Any base cases can be writen as generation of
$S \rightarrow_g \emptyset \vert \epsilon \vert a$ for all $a \in \Sigma \quad from \ R_1’s \ \Sigma$ - Defining the more complex rules requires combining two rules. The recursive expression based on these two base rules can start with:
$S \rightarrow_g A $ (some expression)
$S \rightarrow_g B $ (another expression)
and combined to generate more complex expressions:-
Alternation:
$S \rightarrow_g S_1 \vert S_2 $ (equivalent to A + B for some A, B) -
Concatenation:
$S \rightarrow_g S_1 S_2 $ (equivalent to A B for some A, B) -
Kleene:
$S \rightarrow_g S_1 S \vert \epsilon $ (equivalent to $ A^* $ for some A)
-
Approach 2: RL’s are a special case of CFLs
You can convert any DFA into an equivalent CFG as follows.
- Make a variable $S_i$ for each state $q_i$ of the DFA.
- Add the rule $S_i$ → $aS_j$ to the CFG if $\delta (q_i,a) = q_j$ is a transition in the DFA.
- Add the rule $S_i$ → ε if qi is an accept state of the DFA.
- Make $S_0$ the start variable of the grammar, where $q_0$ is the start state of the machine.
Verify on your own that the resulting CFG generates the same language that the DFA recognizes.
Activity 1 [2 minutes]:
Try to build your own CFG. One that “Accepts” the language: \(L = \{ w \in \Sigma^* \vert w \ has \ an \ odd \ number \ of \ 1s \}\)
(Wait; then Click)
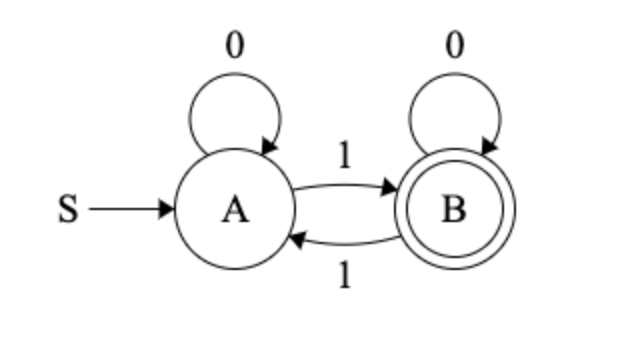
if A is $S_0$ and B is $S_1$: $$ \begin{alignat}{2} S &\rightarrow_g S_A \\ S_A &\rightarrow_g 0S_A \\ S_A &\rightarrow_g 1S_B \\ S_B &\rightarrow_g \epsilon \\ S_B &\rightarrow_g 0S_B \\ S_B &\rightarrow_g 1S_A \\ \end{alignat} $$
How do we prove there are languages that are NOT (beyond) CFLs?
How did we do this back when we did it for RLs?

- the middle part is not too big
- v and y (the repeating parts) are not both simultaneously empty
- repeating v and or y we will keep us in the language
Note that RLs are a special case of Context-Free-Languages (without the $uv^i$) part.
So, if we have a pumping lemma for CFGs, is there a “Machine” equivalent to the Finite Automatons as well?
We’ll see those next class.
Proving a language is NOT context-free

What does your untuition say? Is it a CFL?

Remember:
- Given a structure of $w = uvxyz$, and $ \mid vy \mid \geq 1$
- We want to find an $i$ for which a word $uv^ixy^iz$
does not have a prime length ( $ \mid uv^ixy^iz \mid $ is not prime ) after being “pumped” some number of times. - Here, we can start with a word $w$ with length $p\geq N $ ($N$ provided by the pumping Lemma)
- Now, the trick is to pump the pattern some number of times so that we can prove that the final length is NOT prime!
-
Ideas?
answer:(Wait; then Click)
Steps:
- The length of a word $\mid uv^ixy^iz \mid $ is the length of $ \mid w \mid $ plus any added repetitions of $v$ and $y$
- So, $ \mid uv^ixy^iz \mid $ is $ \mid w\mid + (i-1)\mid vy \mid $
- Since we said $w$ is in PRIMEAL, then $ \mid w\mid $ is some prime number $p\geq N $.
- Then, $ \mid uv^ixy^iz \mid = \mid w\mid + (i-1)\mid vy \mid = p + (i-1)\mid vy \mid$
- Now, What possible choice of $i$ could we choose to cause the overall length to be provably NOT prime ?
Answer Below:
(Wait; then Click)
If we choose $i$ so that the $i-1$ is equal to $p$ in the following expression: $$ \mid uv^ixy^iz \mid = \mid w\mid + (i-1)\mid vy \mid = p + (i-1)\mid vy \mid $$ Then substituting $i-1$ for $p$ ( by making $i = p-1$), we would get: $$ \mid uv^ixy^iz \mid = \mid w \mid + (i-1)\mid vy \mid = p + p\mid vy \mid \\ = p (1+\mid vy \mid) $$ which means that, after pumping, the word is divisible by $p$! and therefore, not of prime length.
Why are CFGs important?

check the article out: https://www.nature.com/articles/nature04675



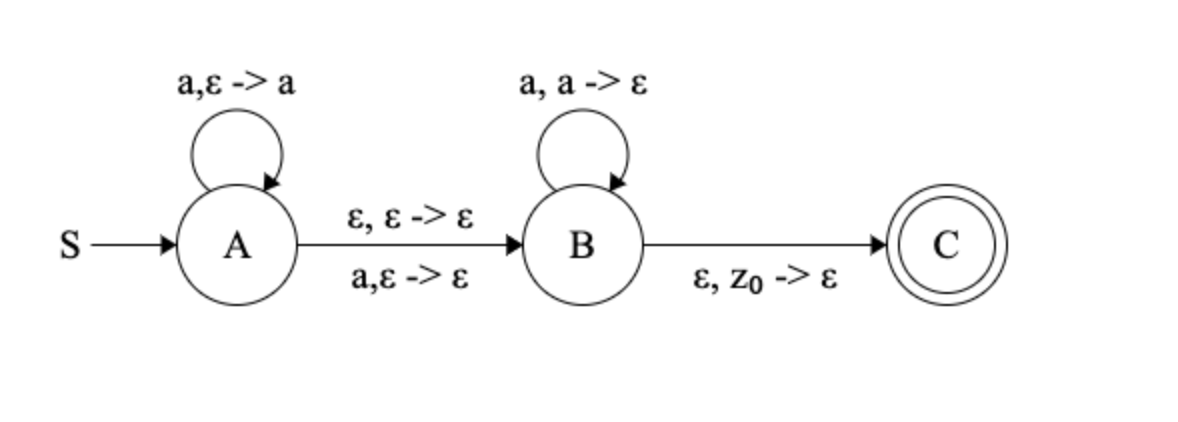
Push-Down Automata

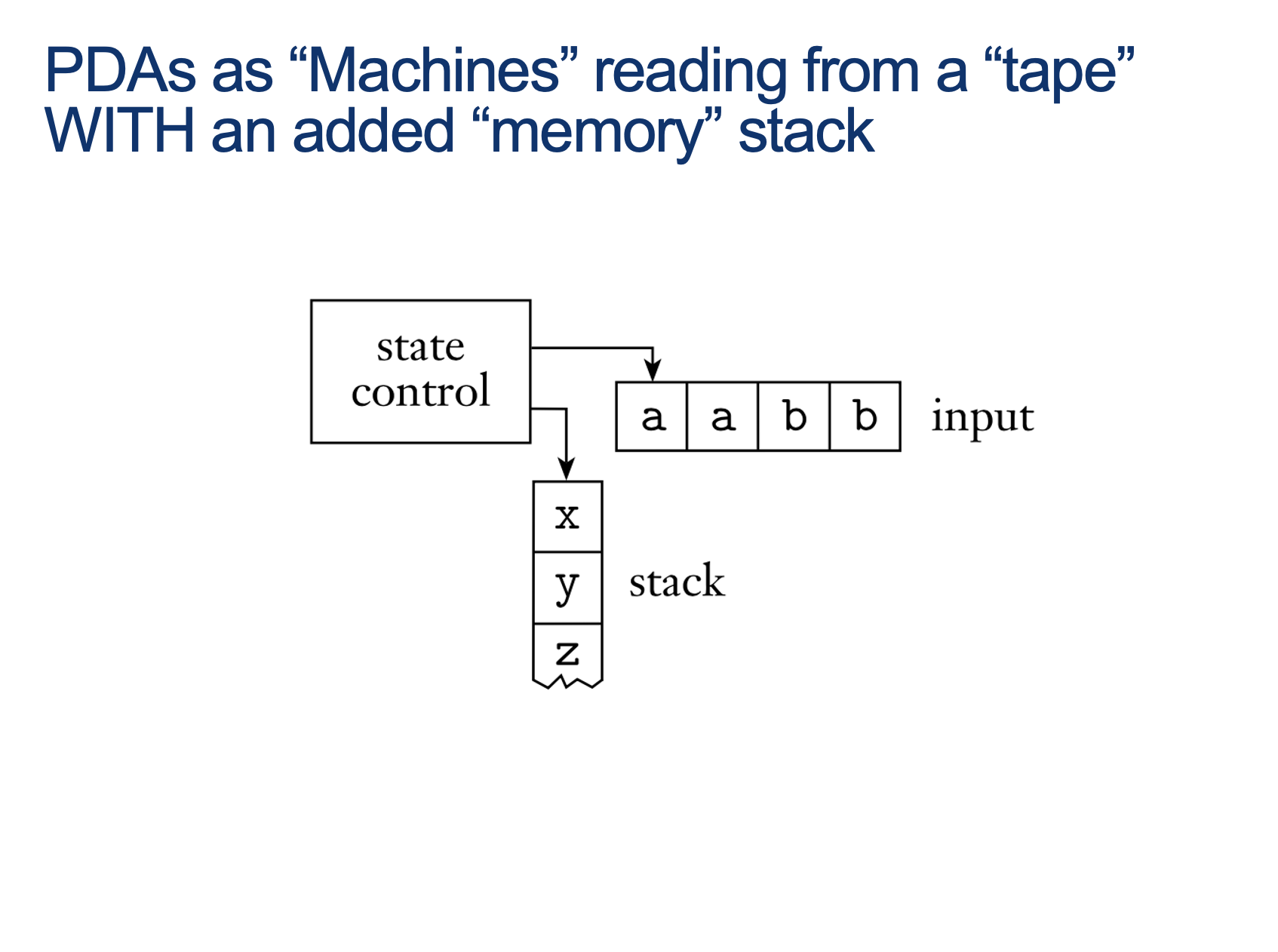

Activity 2 [2 minutes]:
What is the language that these rules are describing?
(Wait; then Click)
- are these a valid words? $\{ \epsilon, 01, 0011, \dots \} $
- We know this language!! What is it called?
Now, let's try to buid an automaton that can keep track of all of this

Notes
- we need a notation for READ, POP and PUSH… we’ll use: $ READ, POP \rightarrow PUSH$
- we need a symbol for “The stack is currently empty!”… we’ll use $z_0$
- we need to be able to read a symbol without pushing … we’ll use $\epsilon$ in place of PUSH
- we need to be able to read a symbol without popping … we’ll use $\epsilon$ in place of POP
- we need to be able to push without reading a symbol … we’ll use $\epsilon$ in place of READ
- we need to be able to pop without reading a symbol … we’ll use $\epsilon$ in place of READ

So now, let’s draw the PDA for HALF
An example for HALF:
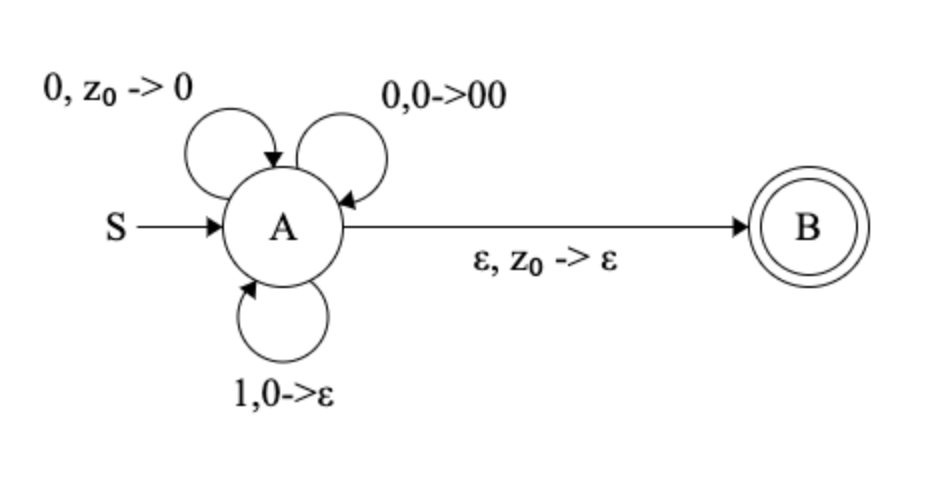
And in a “compressed notation”:
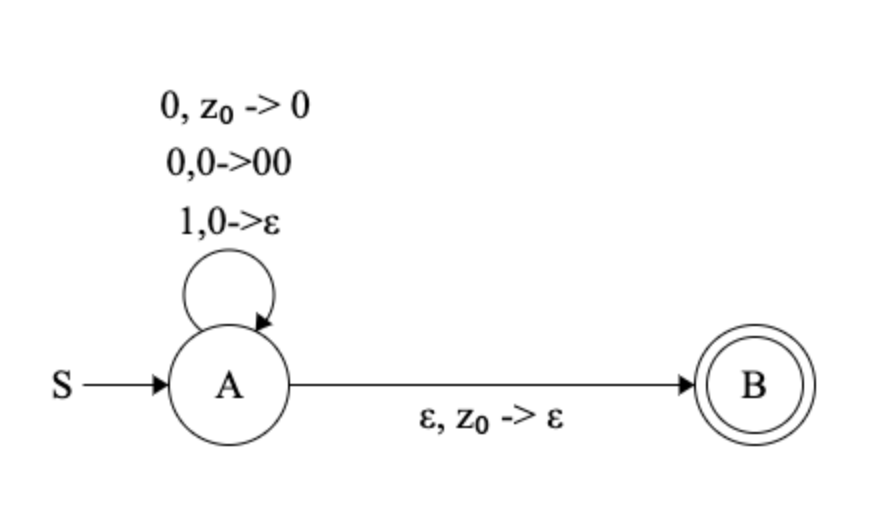

Note that we defined an Augmented NON-Deterministic Automaton




Tips:
- Think of phases:
- memorizing
- middle (even or odd)
- replicating in reverse
- write the PDA… and remember it is NON-Deterministic
Activity 3 [2 minutes]:
Build the PDA for PAL
(Wait; then Click)