Lecture Notes 06: Non-Deterministic FAs and FA Properties

Outline

This class we’ll discuss:

• Non-Deterministic FAs (NFAs)
• NFA Properties

---

A Slideshow:

GUIDED NOTES (Optional)

Nondeterminism

Let’s check a small video fragment from MinutePhysics.

The part we are interested in is the fact that there is a way to:

• Let multiple parallel options happen at the same time!
• As long as any of them succeeds, all “timelines” collapse and the word is accepted.

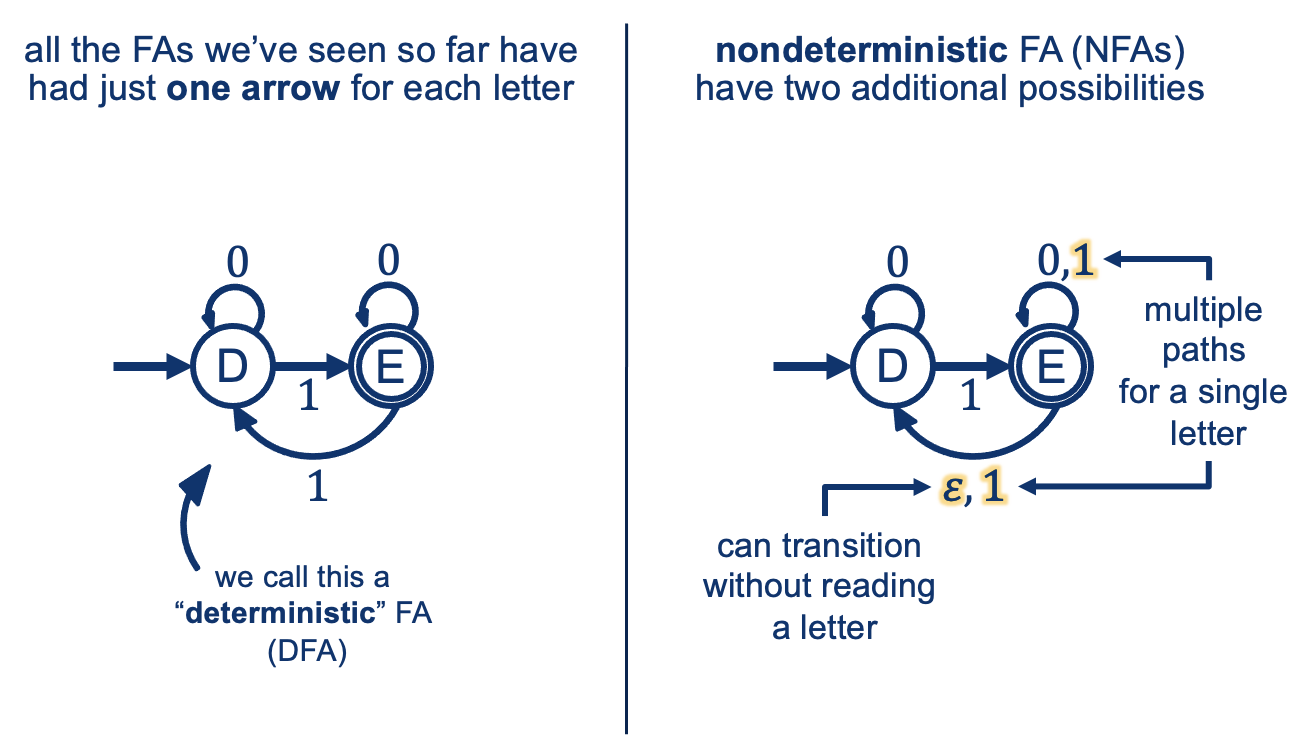
Think of it as having the option of “cloning yourself” into multiple word checkers… each checking one possible path.

We “split” or “clone” each time we:

• see an \(\epsilon\) (or free jump without consuming a symbol), or
• each time we see multiple paths for the same symbol.

Example

Notice that for the example word \( w = 011 \) , the sequence of states is:
\( D \xrightarrow{0} D \xrightarrow{1} E \dots \) and then we have a split!!

• One path continues with: \( D \xrightarrow{0} D \xrightarrow{1} E \mathbf{ \xrightarrow{1} D }\) (Rejected) …
• Another path continues with: \( D \xrightarrow{0} D \xrightarrow{1} E \mathbf{ \xrightarrow{1} E } \) (Accepted) …
• Yet another path continues with: \( D \xrightarrow{0} D \xrightarrow{1} E \mathbf{ \xrightarrow{\epsilon} D \xrightarrow{1} E } \) (Accepted)
• The last path continues with: \( D \xrightarrow{0} D \xrightarrow{1} E \mathbf{ \xrightarrow{\epsilon} D \xrightarrow{1} E \xrightarrow{\epsilon} D} \) (Rejected)

---

NFAs Formal Definition

Activity 3 [2 minutes]:

Why would this be useful at all?

Remember Union?

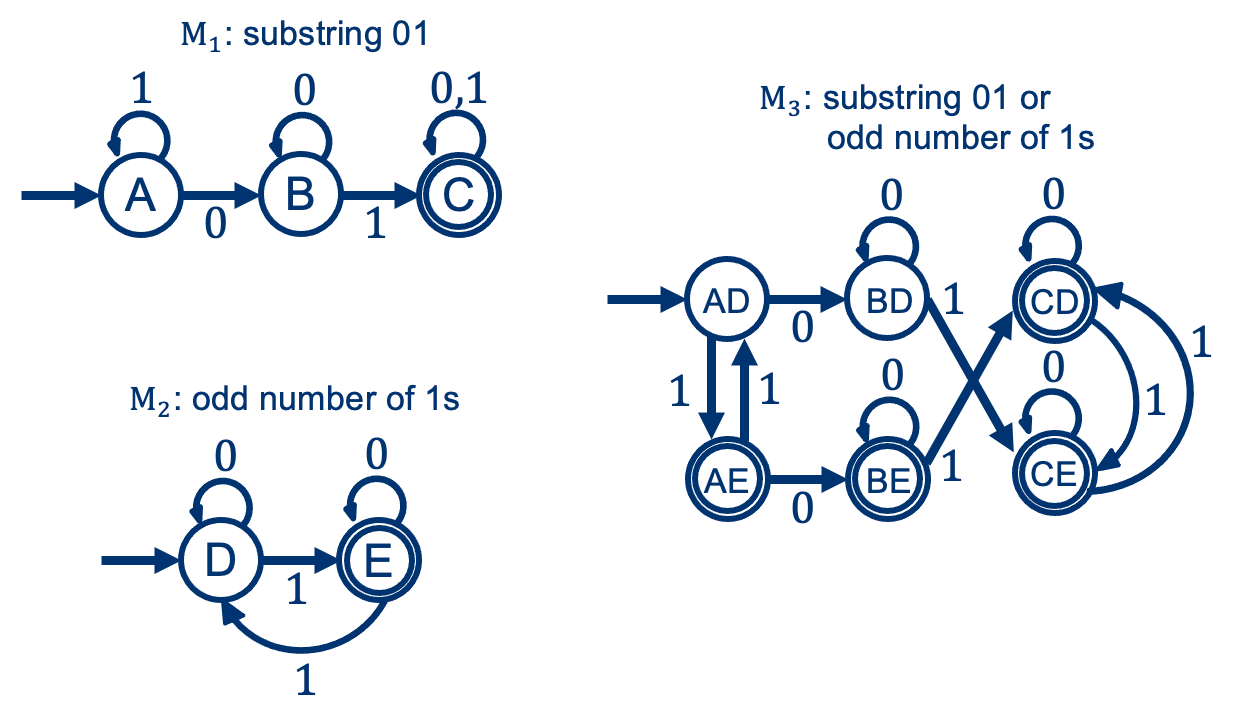
With an NFA:

So how do NFA’s Compute?

---

NFA computation (tree)

We can visualize what happens with the computation of a string with an NFA by building a NFA computation Tree.

This is like “unrolling an FA as we walk it into paths”, except with two extra rules:

1. You add a possible path into a “next” state for every outgoing symbol option, and
2. You add a possible path into a “next” state any states we might get to through an arrow labeled with \(\epsilon\)

An Example:

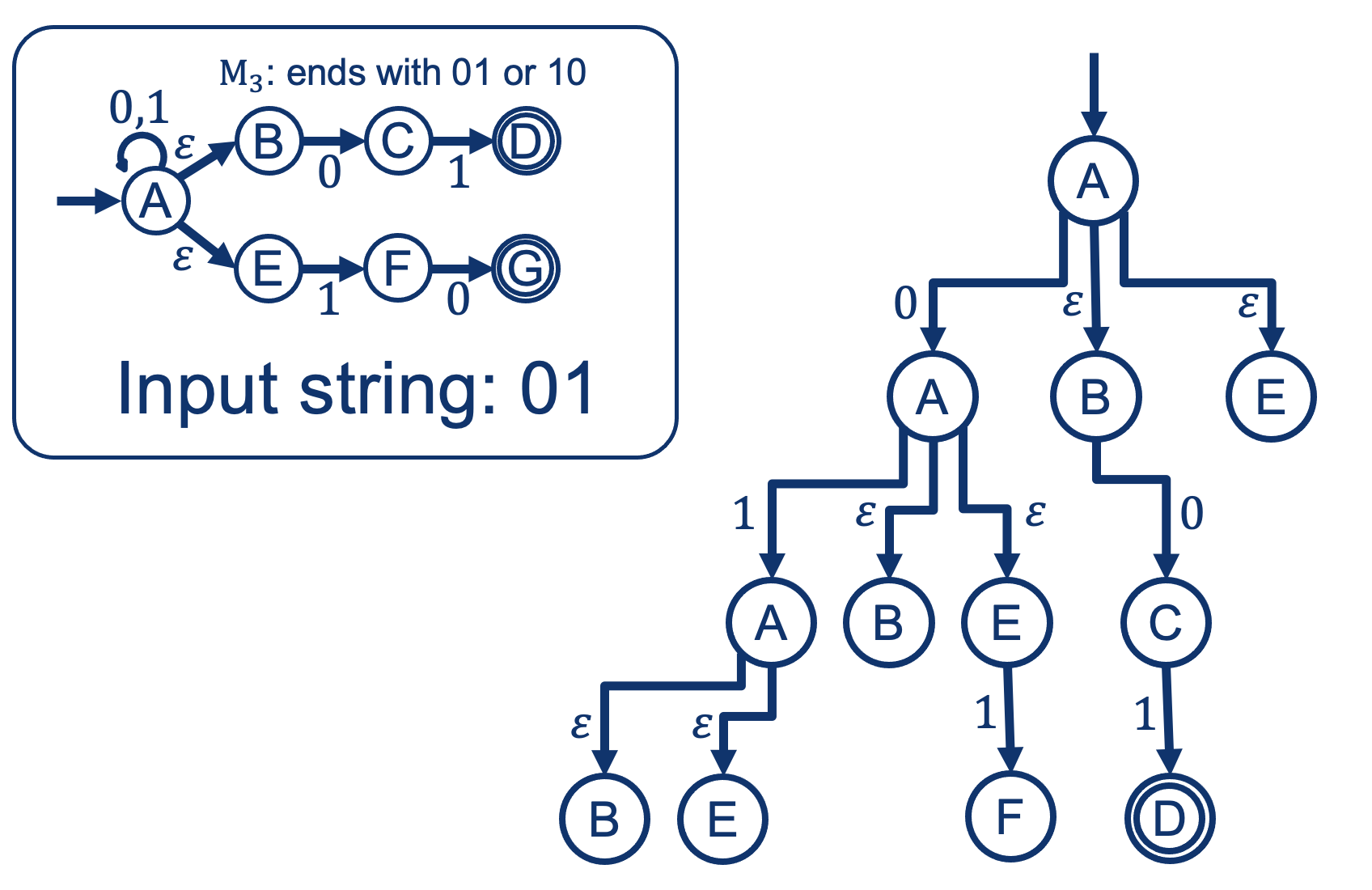
Activity 4 [2 minutes]:

Does the above example Accept or Reject string:   \( 0 \; 1 \)?

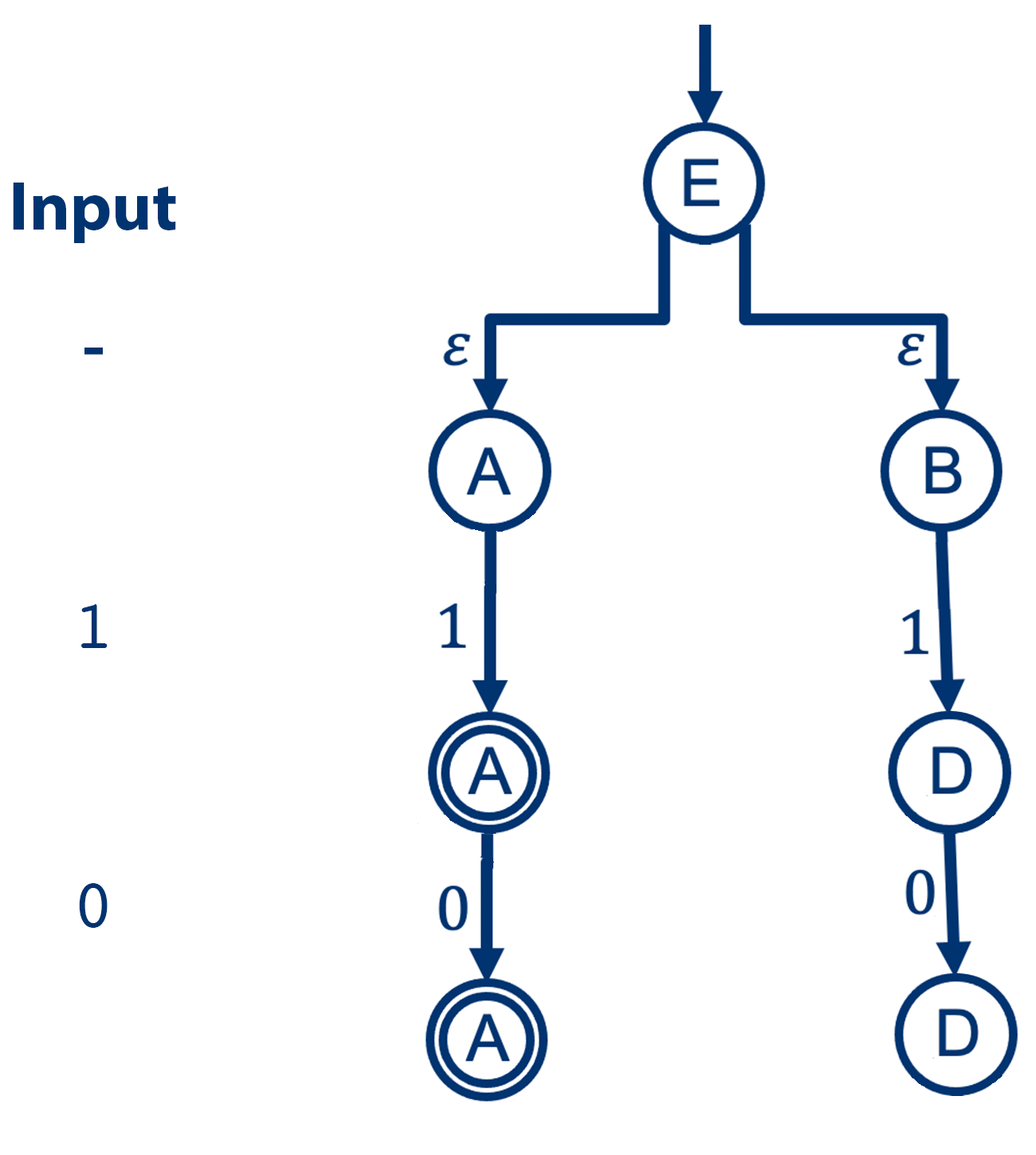
Activity 5 [2 minutes]:

Build the computation tree for the Union example for the string   \( 1 \; 0 \)

The example is repeated here for your convenience (you’re welcome)

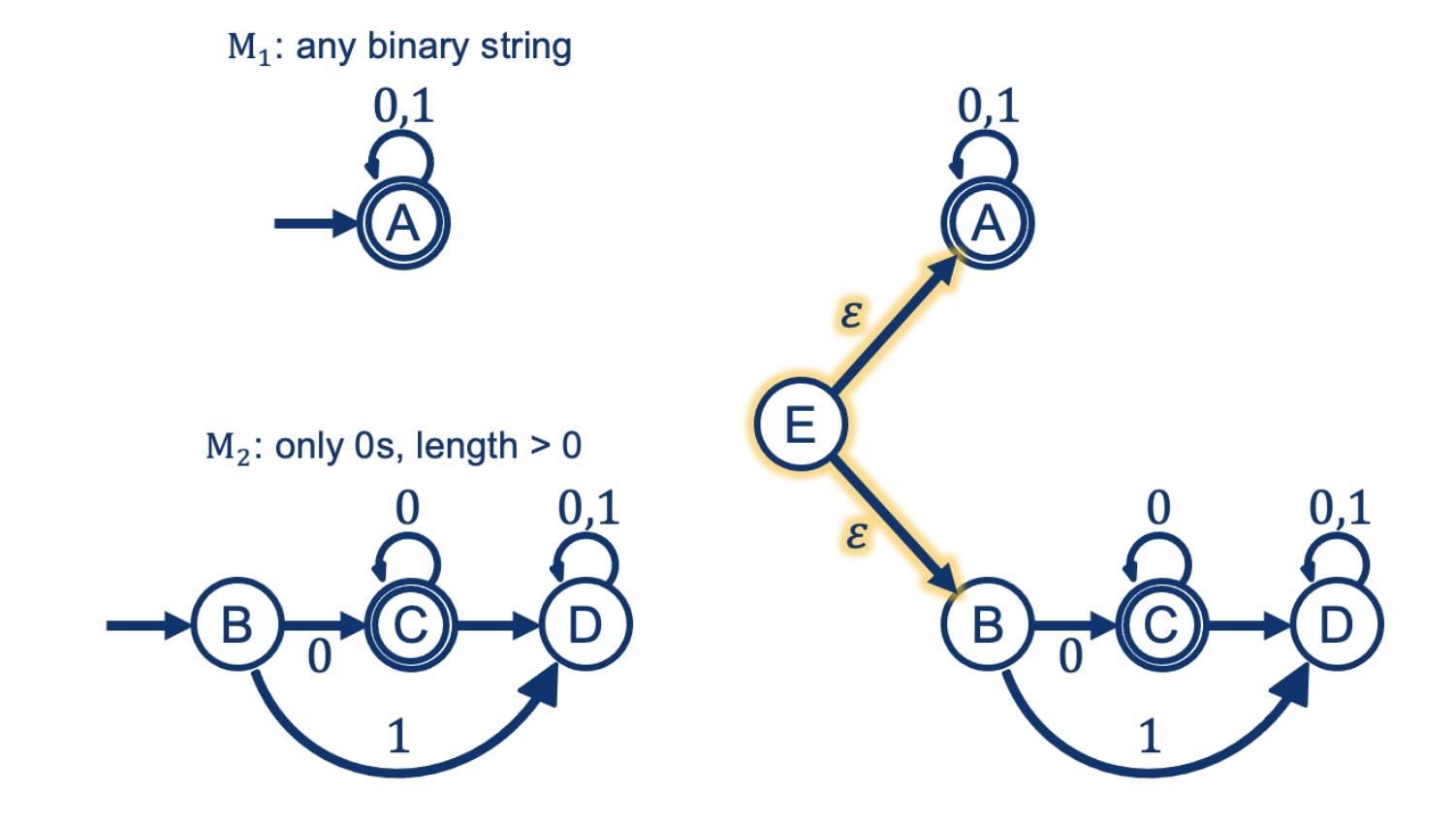
“Walk” the NFA and add a path for every possible choice (given the symbol read)

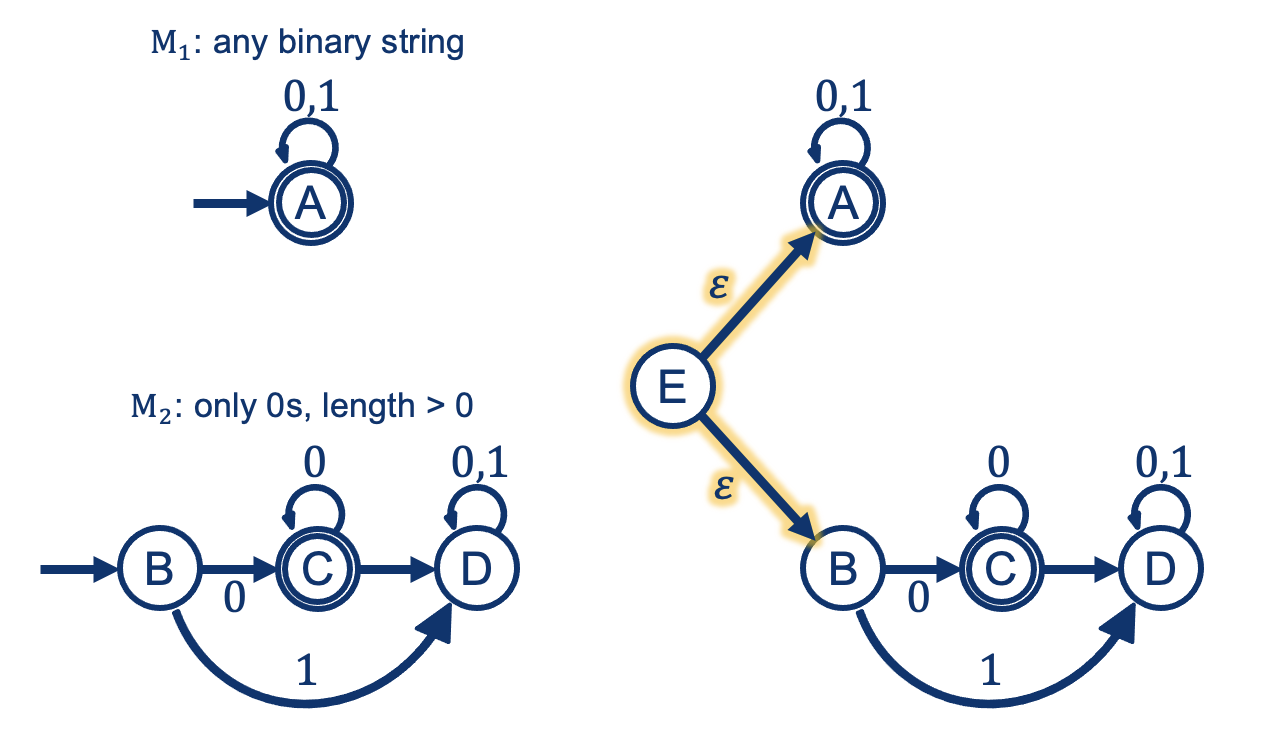
Remember Concatenation?

The problem was we could not “guess” at which part of the string one Machine should accept (reject) and the next begin processing.

With an NFA:

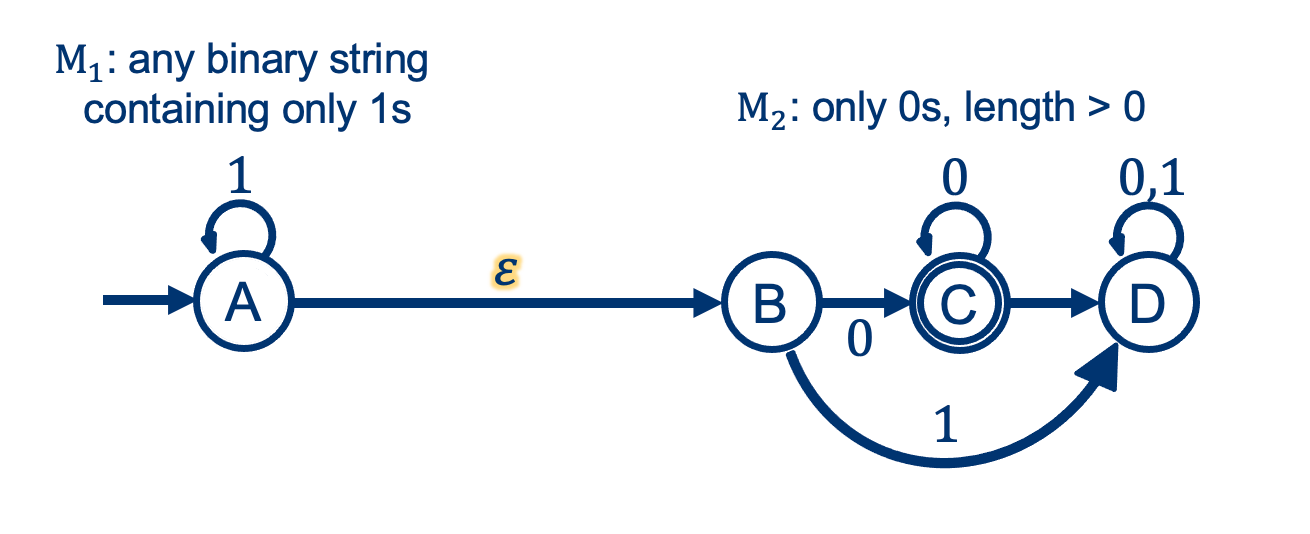
Activity 6 [2 minutes]:

Build the computation tree for the Concatenation example above, given the string:
\( 1 \quad 1 \quad 1 \quad 0 \)