Lecture Notes 20: Reductions and Enumeration

Outline

This class we’ll discuss:

• Recap: Reductions
• Recognizing and Enumeration

---

A Slideshow:

REVIEW Slides:

CLASS Slides

---

GUIDED NOTES (Optional)

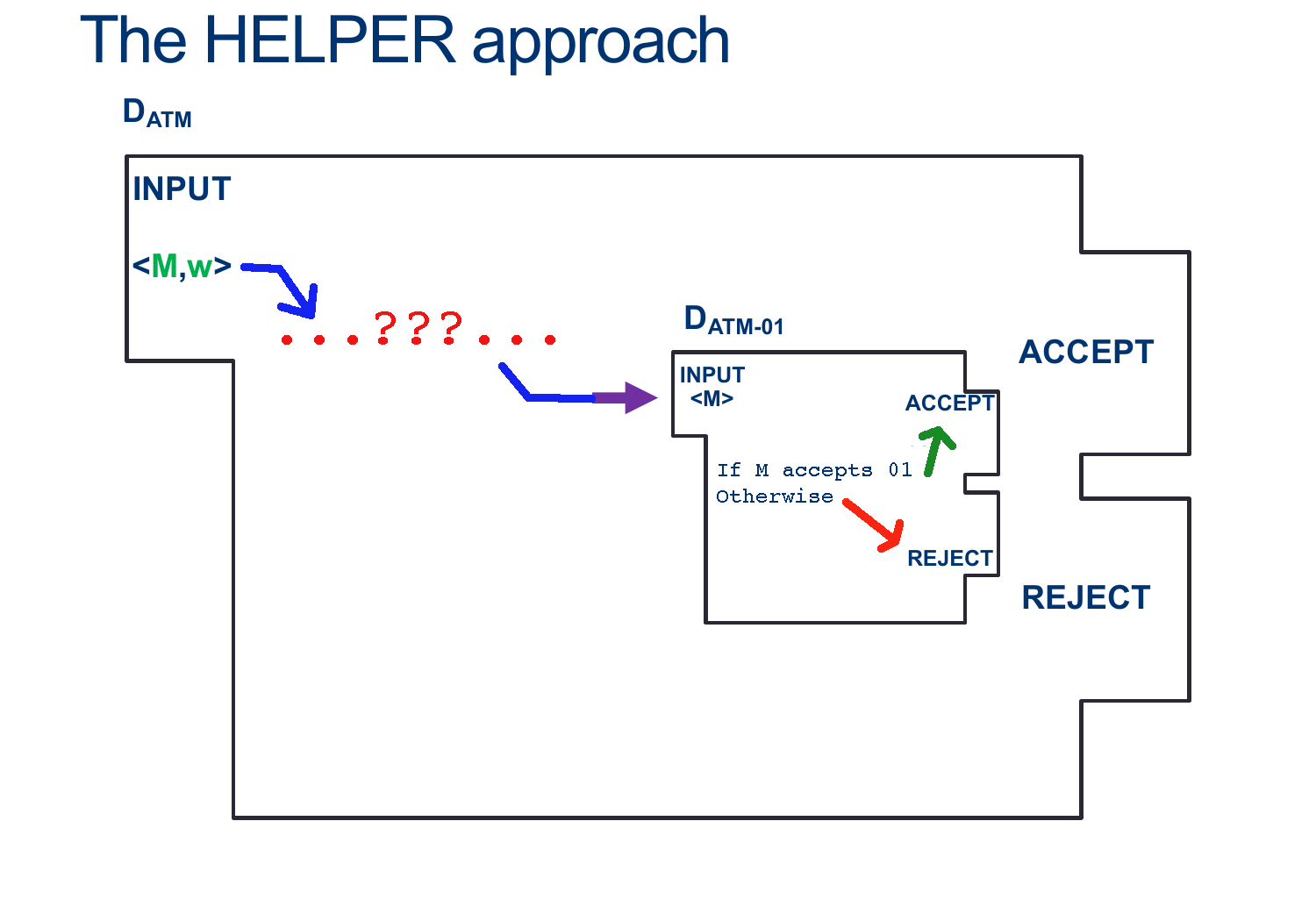
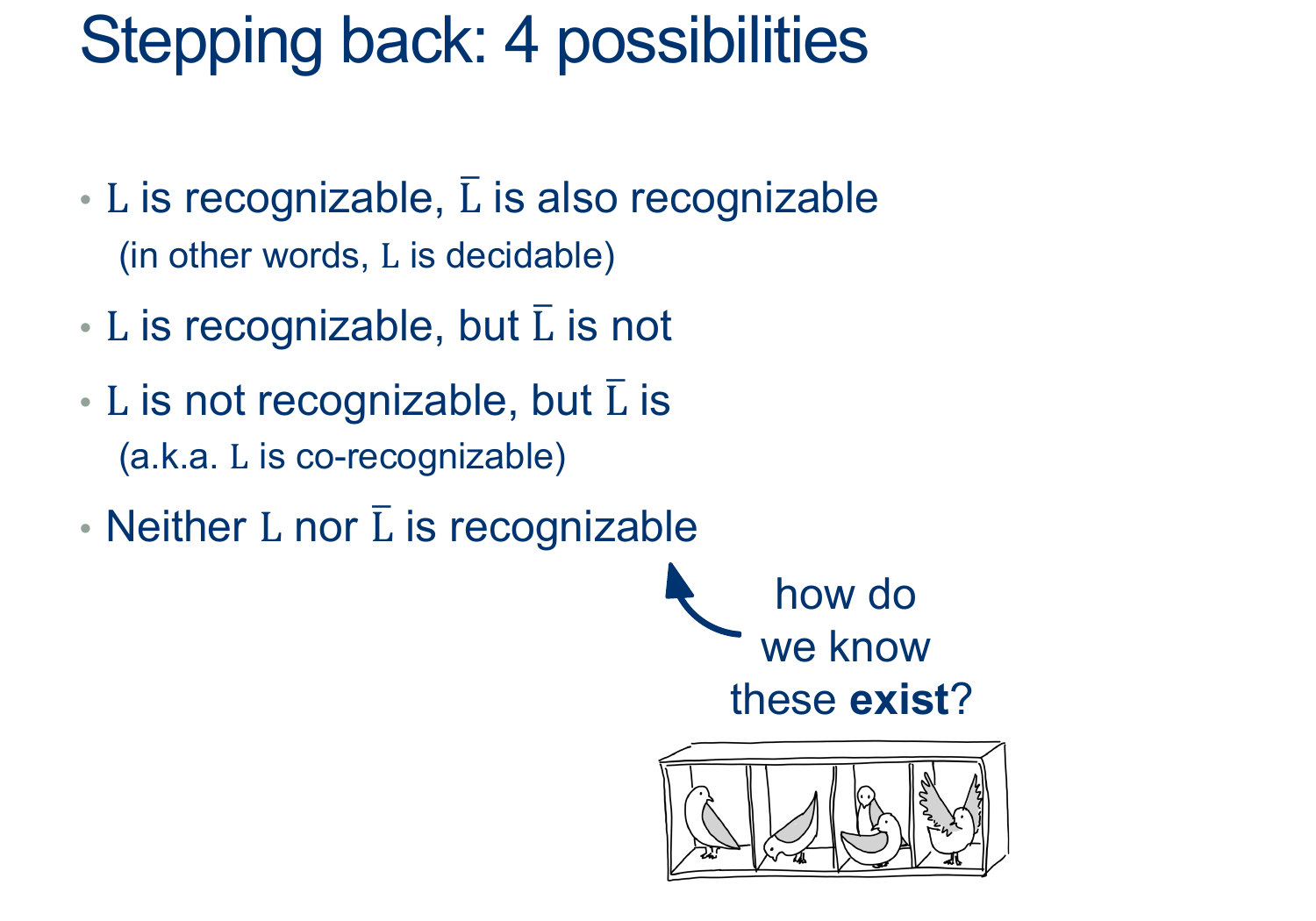
(ATM-01 is at least as hard to decide as ATM)

Note that:

1. IF a machine $D_{ATM}$ existed, it would receive input $ < M, w > $
2. IF a machine $D_{ATM-01}$ existed, it would receive input $ < M > $
3. The order of the proof is:
   1. Assume $D_{ATM-01}$ already exists
   2. We can use it to build another machine that should behave like $D_{ATM}$
   3. This larger machine, should be able to handle input $ < M, w > $
   4. You must somehow get a machine with ONLY $ < M > $ as input to handle the input $ < M, w > $
   5. Note that, as part of the steps, you can build helper machines

Activity 4 [2 minutes]:
In teams, write a Machine that uses $D_{ATM-01}$ to perform the work of $D_{ATM}$ (Wait; then Click)

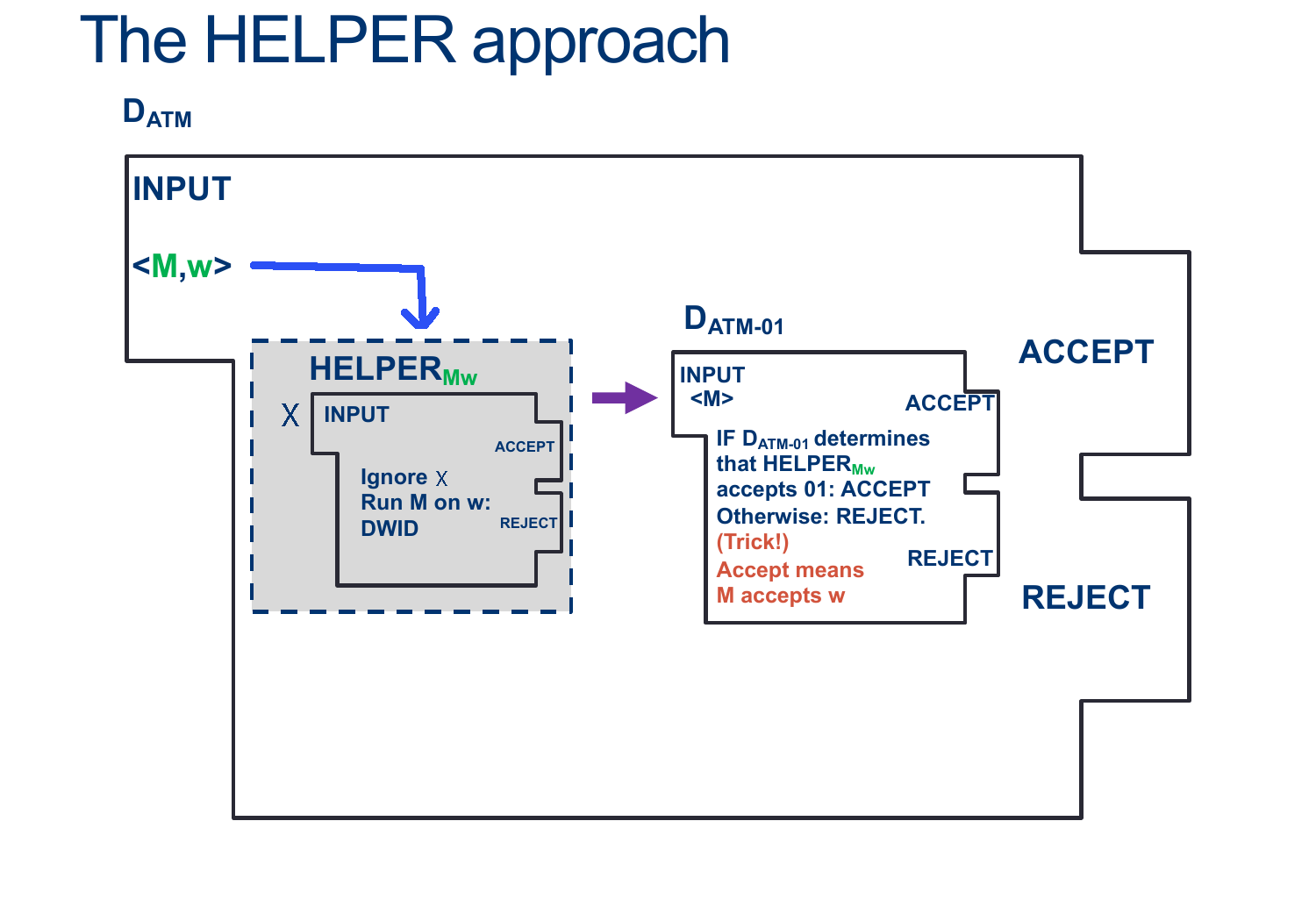
This can be written like this:

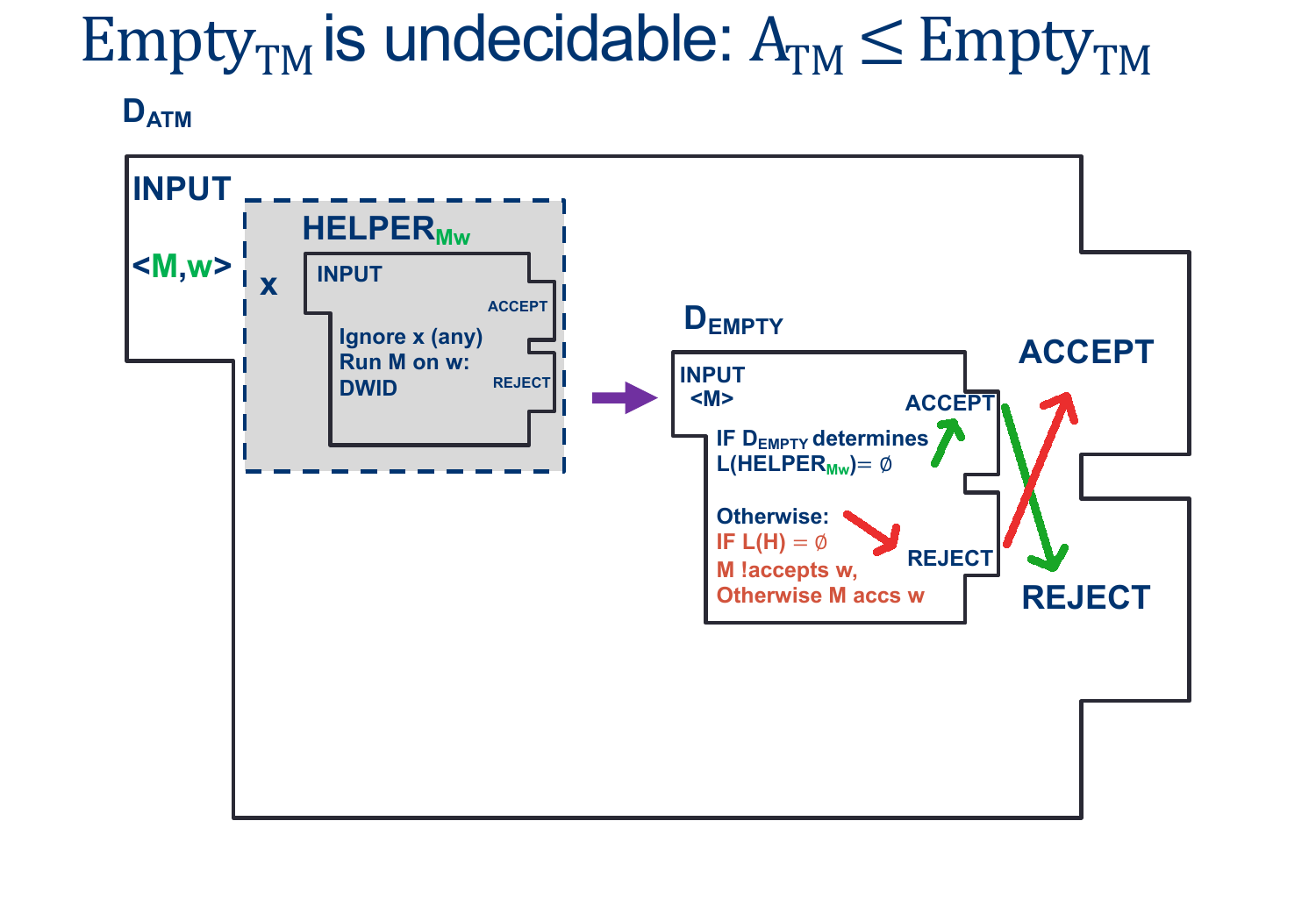
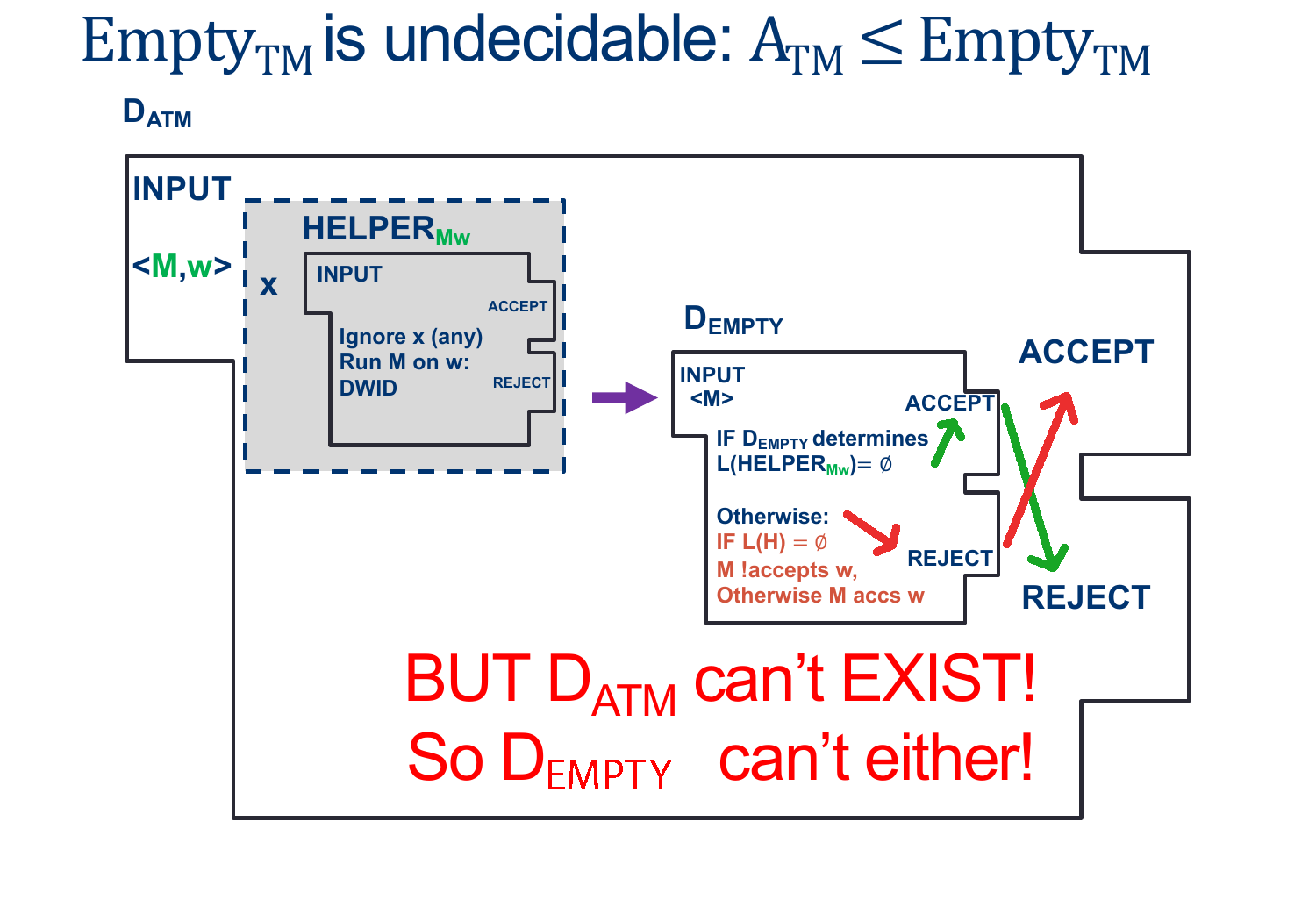
Assume EMPTY-TM is decidable, and so there exists some $D_{EMPTY-TM}$ that decides, for any input $< M >$, whether $L (M) $ is empty.

We’ll design the Machine $D_{ATM} $ as follows:

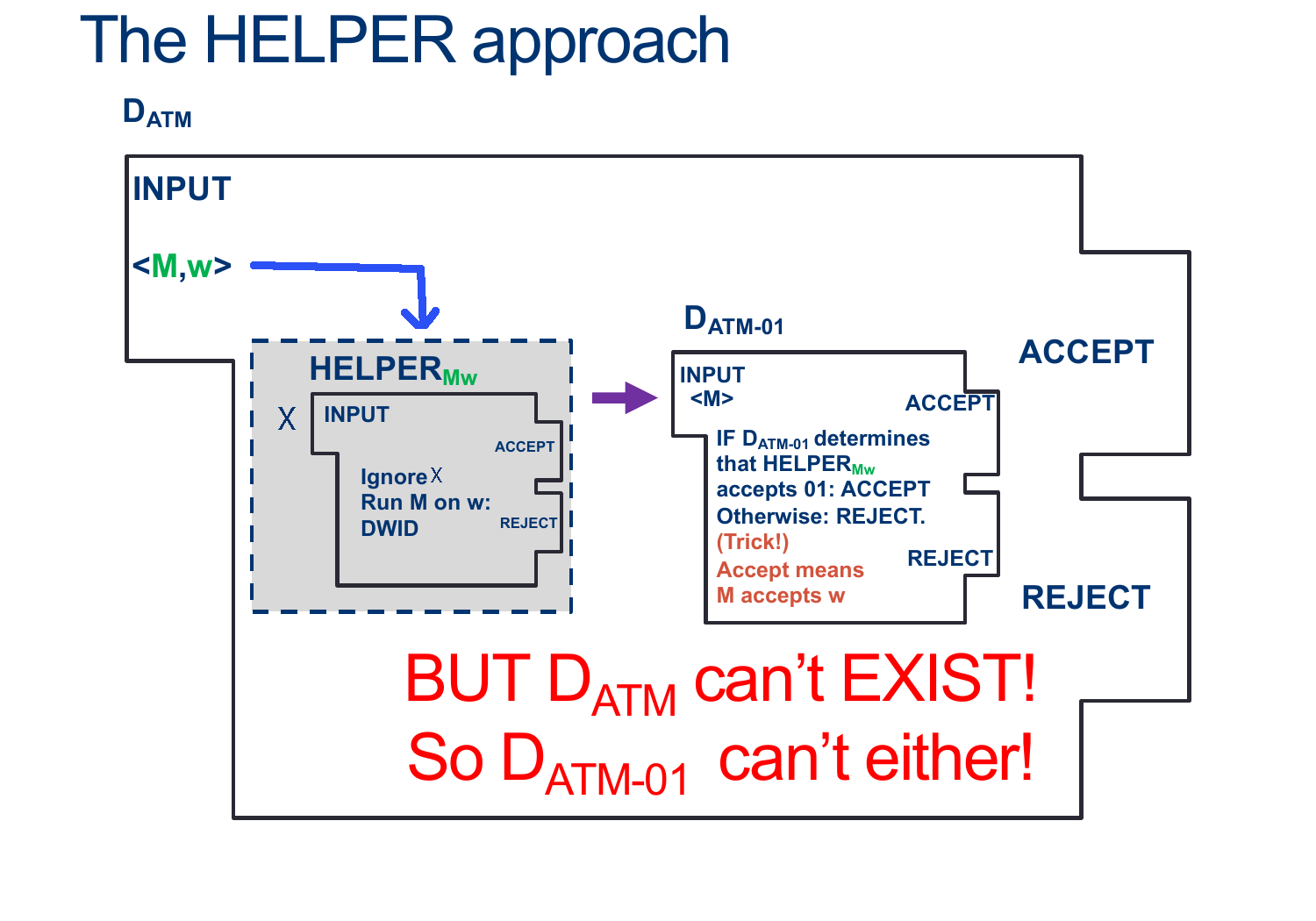
\[\begin{align*} &D_{ATM}:\\ & \text{ On input $ < M, w > $ }:\\ & \text{ Create (but don't run) $HELPER_{M,w}$ such that}\\ & \quad \text{ On input $ < X > $ }:\\ & \quad \quad \text{ Ignore $ < X > $ }\\ & \quad \quad \text{ Run $M$ on $w$ ADWID}\\ & \text{ Now Run $D_{EMPTY-TM}$ on $HELPER_{M,w}$}\\ & \text{ If $D_{EMPTY-TM}$ rejects, invert the result and our machine ACCEPTS}\\ & \text{ If $D_{HALT}$ accepts, , invert the result and our machine REJECTS}\\ \end{align*}\]

As we saw above, the ONLY way $D_{EMPTY-TM}$ Rejects is if $HELPER_{M,W}$ Accepts, which happens ONLY when $M$ accepts $w$.

This means we CAN make $D_{ATM}$ as long as $D_{EMPTY-TM}$ exists.

However, $D_{ATM}$ doesn’t exist…which means $D_{EMPTY-TM}$ CANNOT EXIST EITHER.

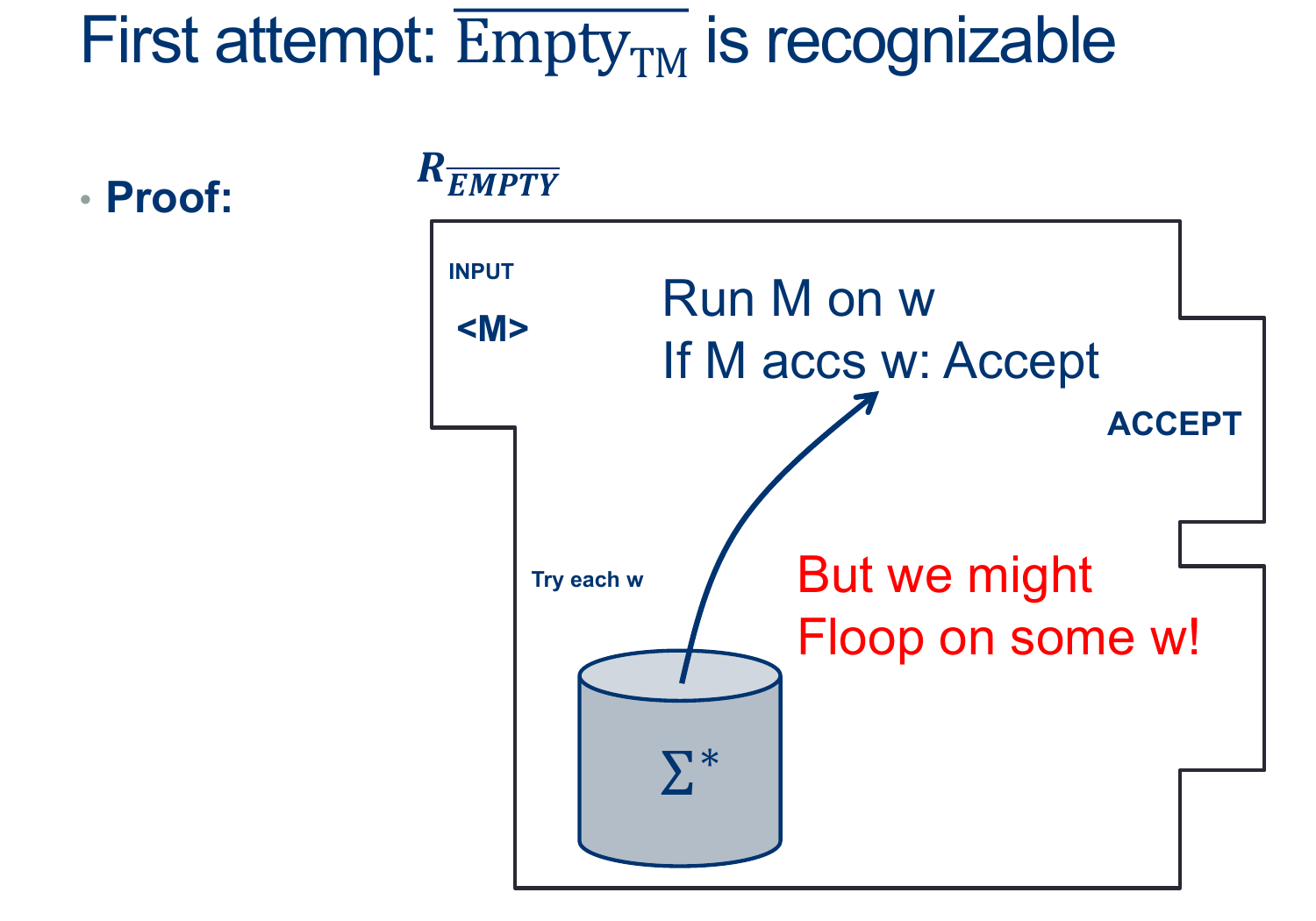
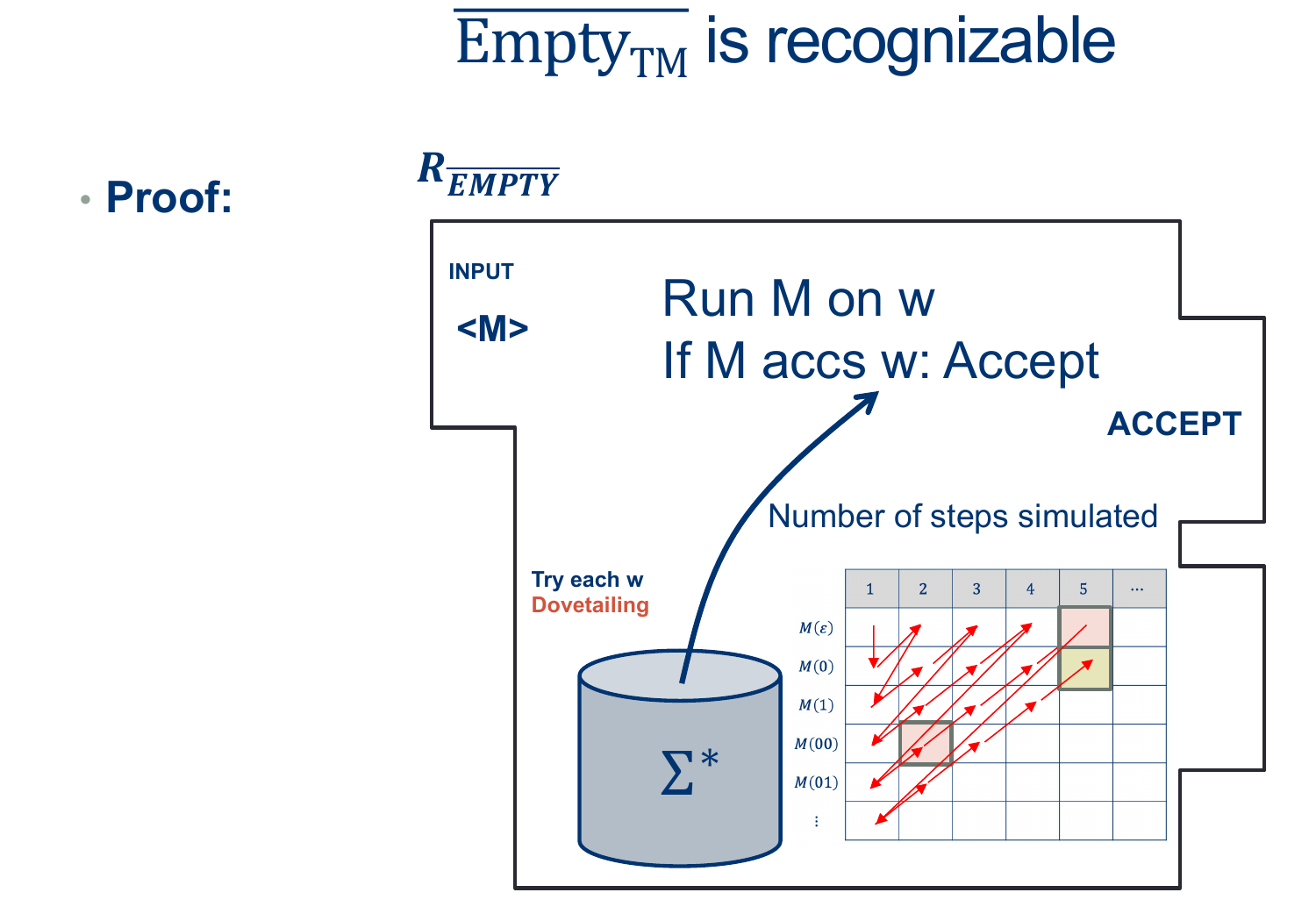
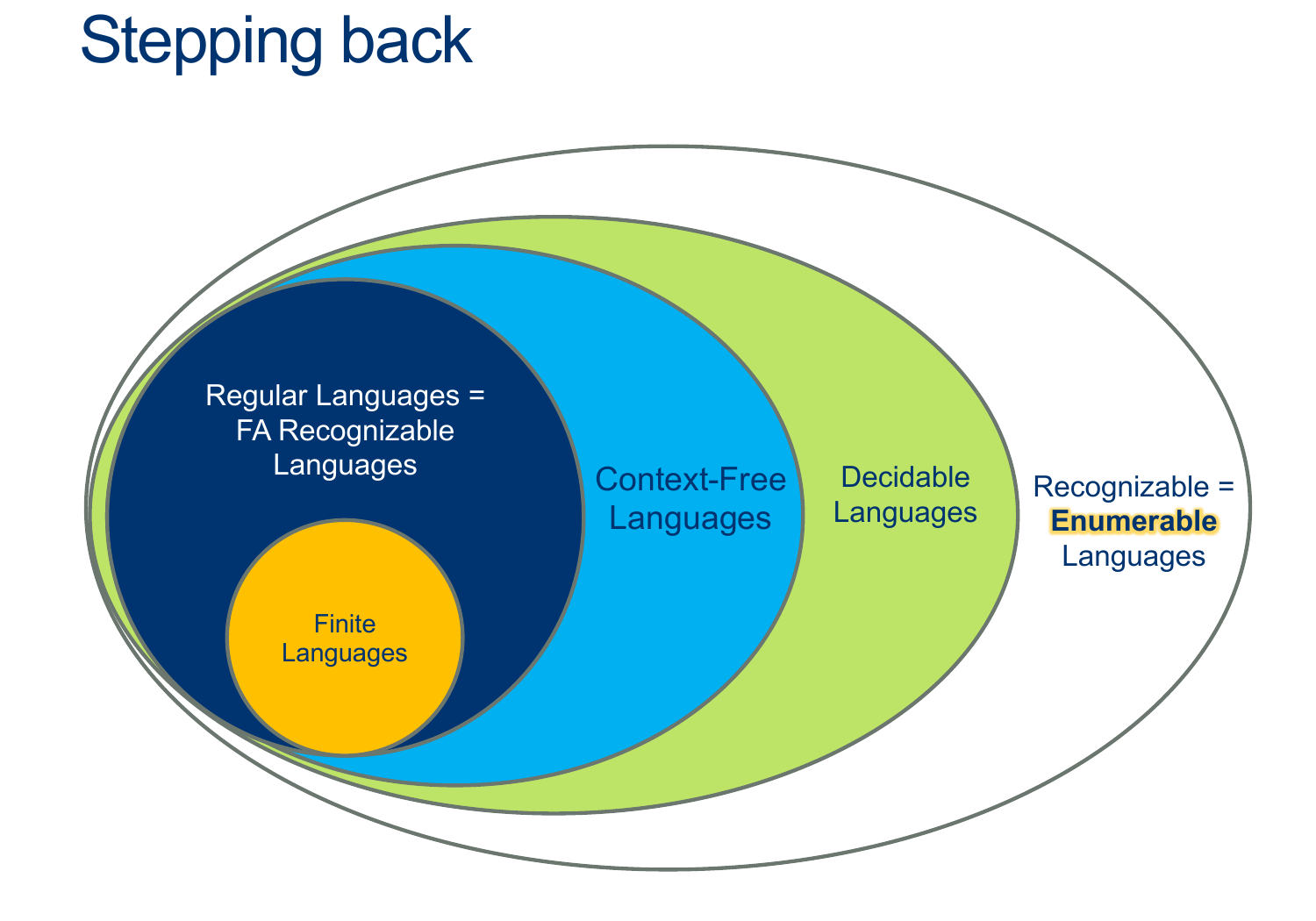
This will lead us to a new way of looking at Recognizers: Enumeration.

Enumeration

Activity 3 [2 minutes] In groups, come up with an algorithm to enumerate $\Sigma^*$?:

Activity 4 [2 minutes] In groups,
How would you prove that, IF you can enumerate a Language, then that language is Recognizable.
(Wait; then Click)

Assume L is enumerable, i.e. there exists some machine E_L that can print out all of Ls words.
Build a machine R_L that uses E_L to print them out one at a time, and compares each one with the input.
As soon as they match, accept.

This machine accepts only words that are in L, and if a word is in L we’re guaranteed to reach it at some point (though it might take awhile).
Thus, it recognizes L. QED.

Undecidability

Intro to Undecidable Problems (Languages)

Problems as Languages

In this class, we have converted “finding a solution to a problem” to “Learning to accept words from a Language”.

In our world, Answering a question means building a machine that recognizes the language-version of that question.

Example problem:
“Can you come up with a binary string with a pattern of 0s and 1s such that the string is a palindrome”

Example Language-Version:
\(L = \{ w \in \Sigma^* | w^R = w \}\)

Example solution:
(See the CMF, PDA, or TM solutions to this problem)

Questions about Machines

Often we’ll ask questions about the machines we’ve seen so far.

Again, answering a question means building a machine that recognizes the language-version of that question.

So, a problem like:
“Find the set of Turing Machines that have up to 5 states”,
can be rephrased as finding the Language:

\[L = \{ < M > | M \text{ is a TM and } M \text{ has fewer than 5 states} \}\]

Answering with an Algorithm

How would you “Solve” the problem for:

\[L = \{ < M > | M \text{ is a TM and } M \text{ has fewer than 5 states} \}\]

What could you use to “Solve” (Decide/Recognize) $L$?

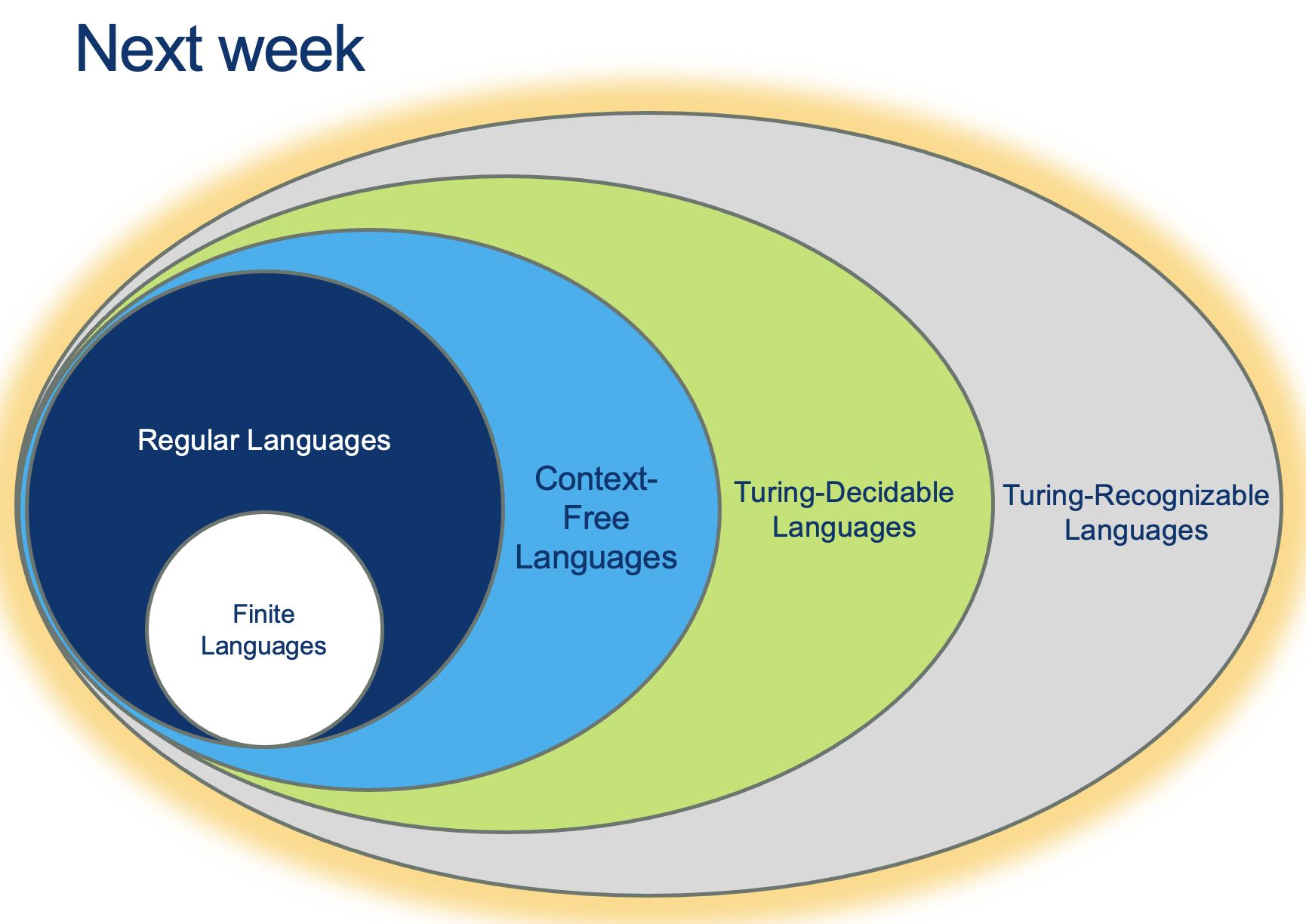
Another Recap (so we don’t get lost)

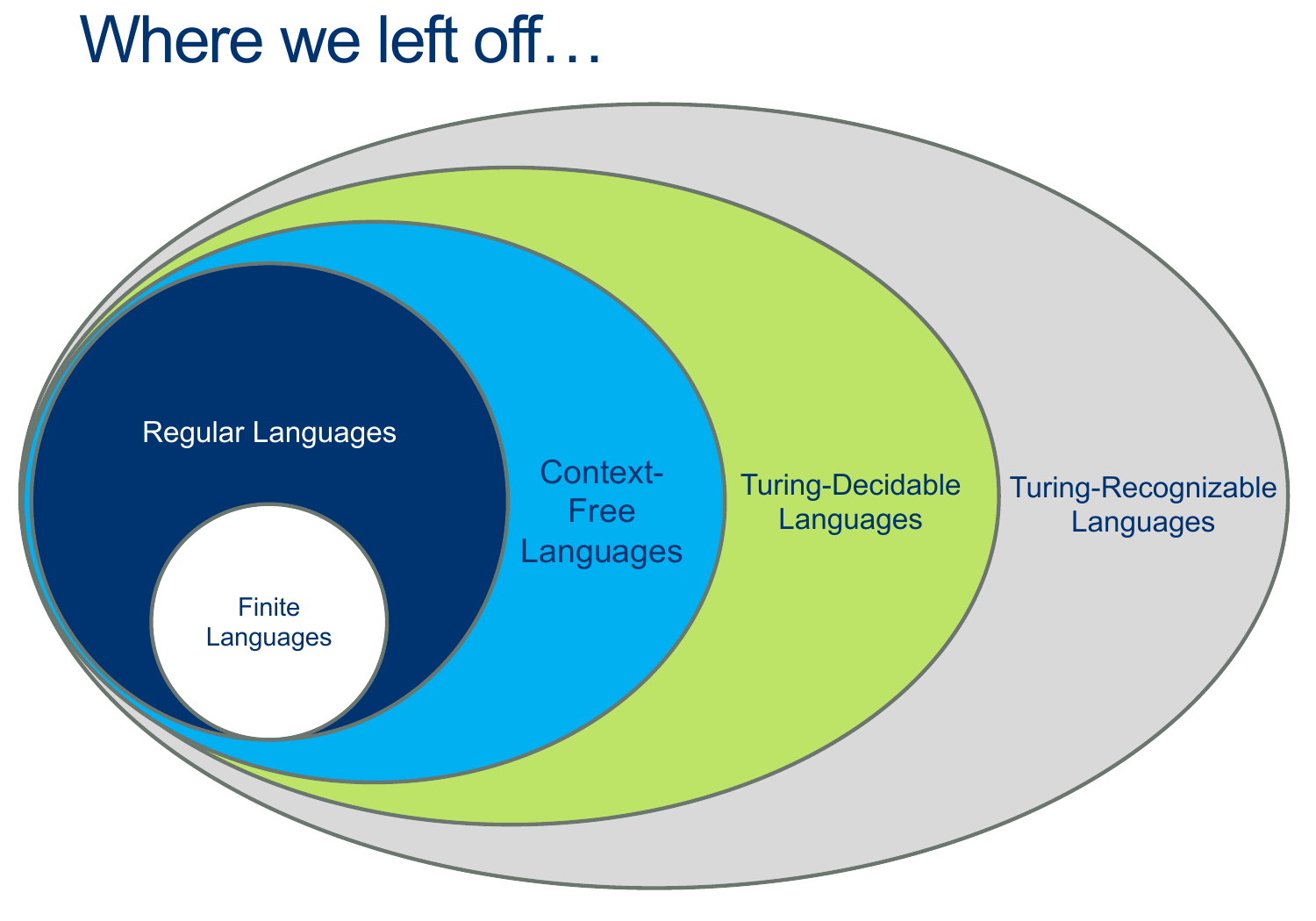
Questions about Machines

Discuss if you could build $D_L$ for the following language:

\[L = \{ < M, w > | TM \; M \text{ accepts } w \text{ in fewer than 10 steps} \}\]

Discuss if you could build $D_L$ for the following language:

\[L = \{ < A > | \text{DFA $A$ accepts an infinite number of words (L(A) is infinite)} \}\]

Discuss if you could build $D_L$ for the following language:

\[A_{TM} = \{ < M, w> | \text{TM $M$ accepts } w \}\]

How about ATM?

Can we come up with a simple proof?

Is ATM decidable?

Discuss if you could build $D_L$ for the following language:

\[A_{TM} = \{ < M, w> | \text{TM $M$ accepts } w \}\]

Can a $D_{ATM}$ be constructed such that:

1. It Accepts any $w $ such that $w \in A_{TM}$

AND

1. It Rejects any $w $ such that $w \notin A_{TM}$

Step 1: Assume Is ATM is Decidable Now try to use this “fact” to arrive at a contradiction

Consider the Machine $M_{OPPOSITE} ( < M> )$

\[\begin{align*} &M_{OPPOSITE}:\\ & \quad \text{ On input $ < M > $ }:\\ & \quad \text{ Simulate $D_{ATM} \; on \; < M , < M > > $}\\ & \quad \text{ If $D_{ATM}$ accepts, REJECT. }\\ & \quad \text{ If $D_{ATM}$ rejects, ACCEPT. }\\ \end{align*}\]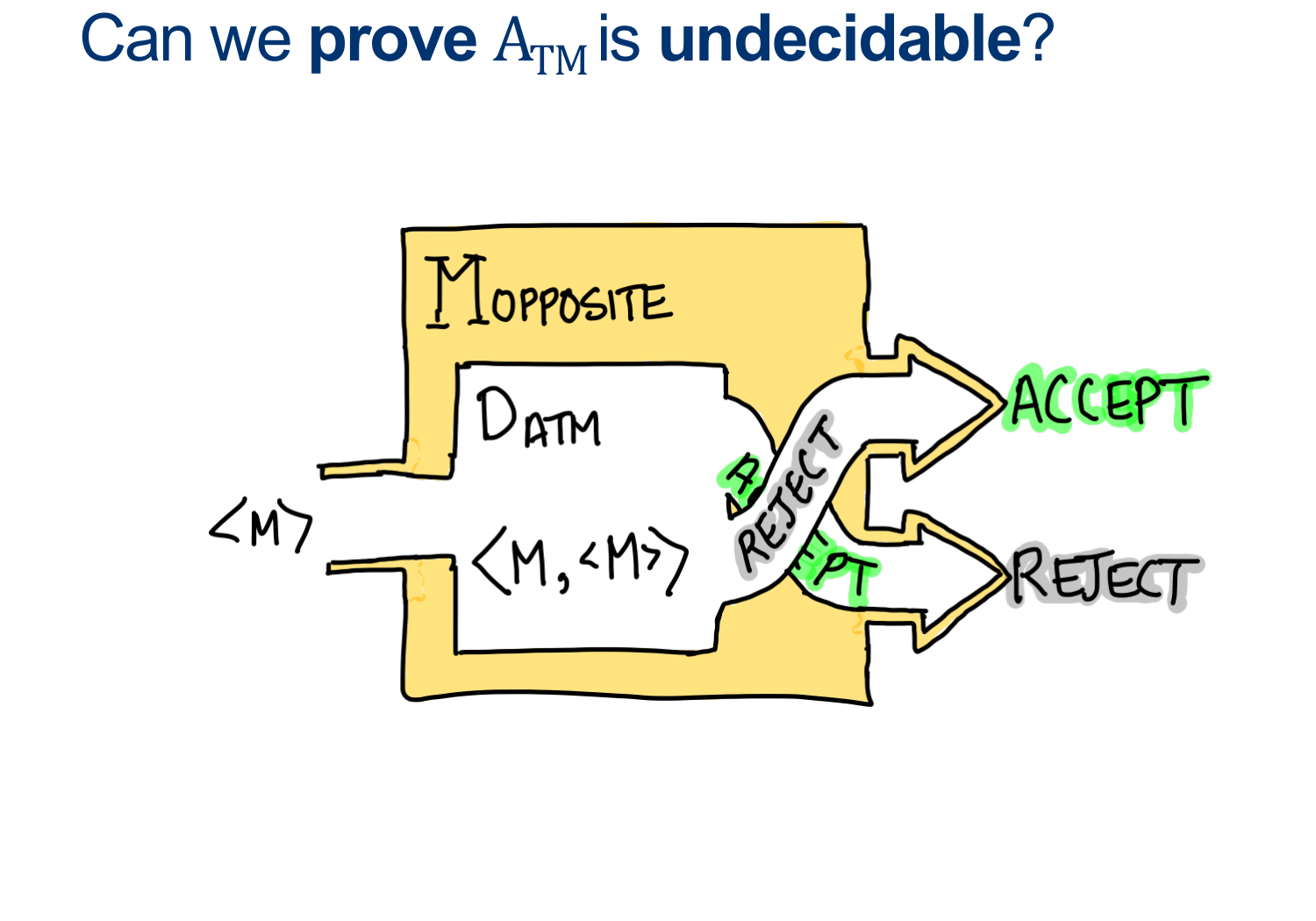

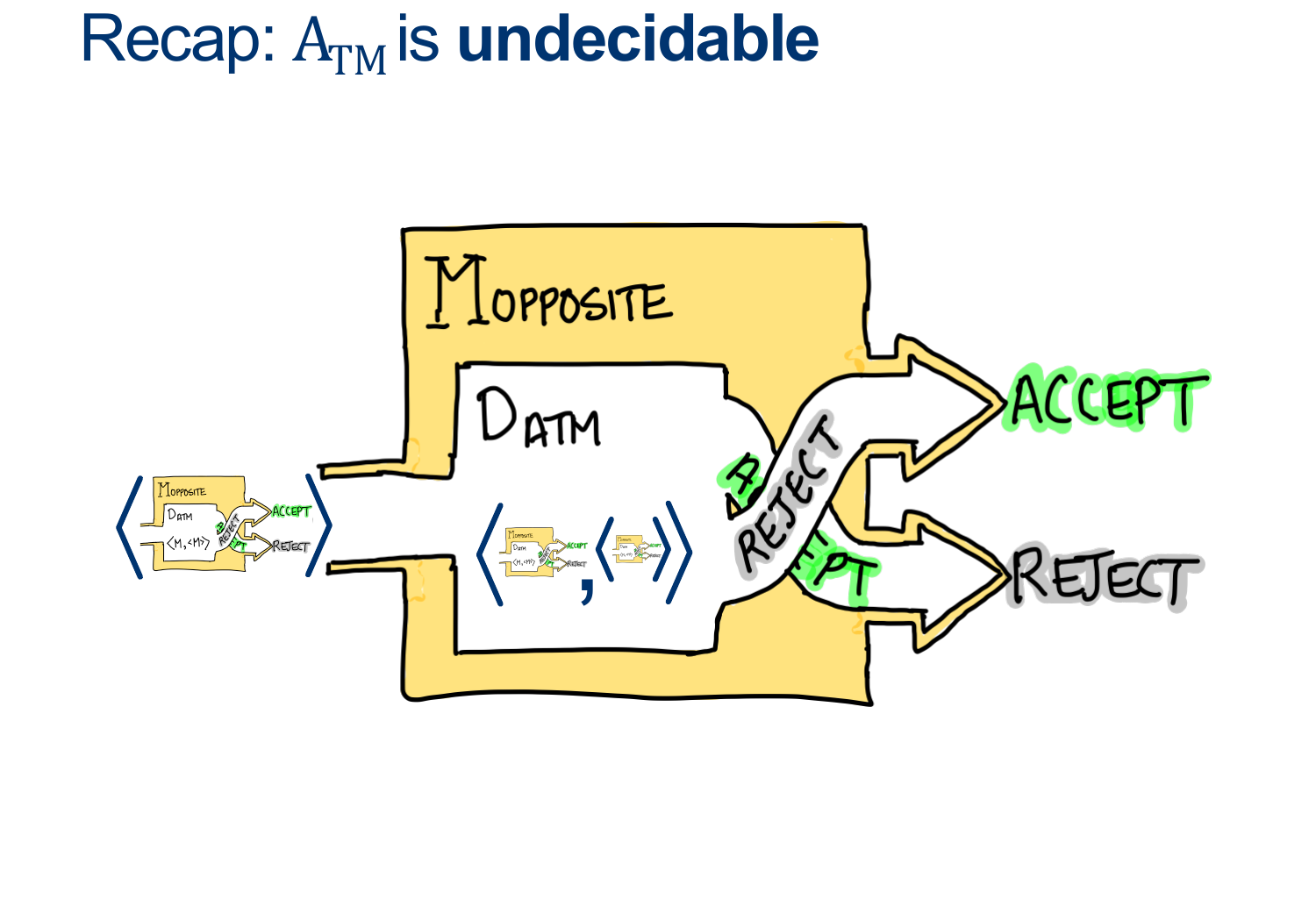
In other words, $ HALT$ is AT LEAST as hard as $ ATM $
(So if we can solve HALT, we can, for sure, solve ATM)

Try it out yourselves first

Think of a way you can get to say:
if we can solve HALT, we can, for sure, solve ATM

–>