Lecture Notes 15:Halting, Deciding, Recognizing
Outline
This class we’ll discuss:
- More on The Halting Problem
- Decidability
- Recognizing
A Slideshow:
GUIDED NOTES (Optional)
Turing Machines and Decidability



(Wait; then Click)
- move both left and right
- write new symbols to the tape
- stop at any point and return an answer

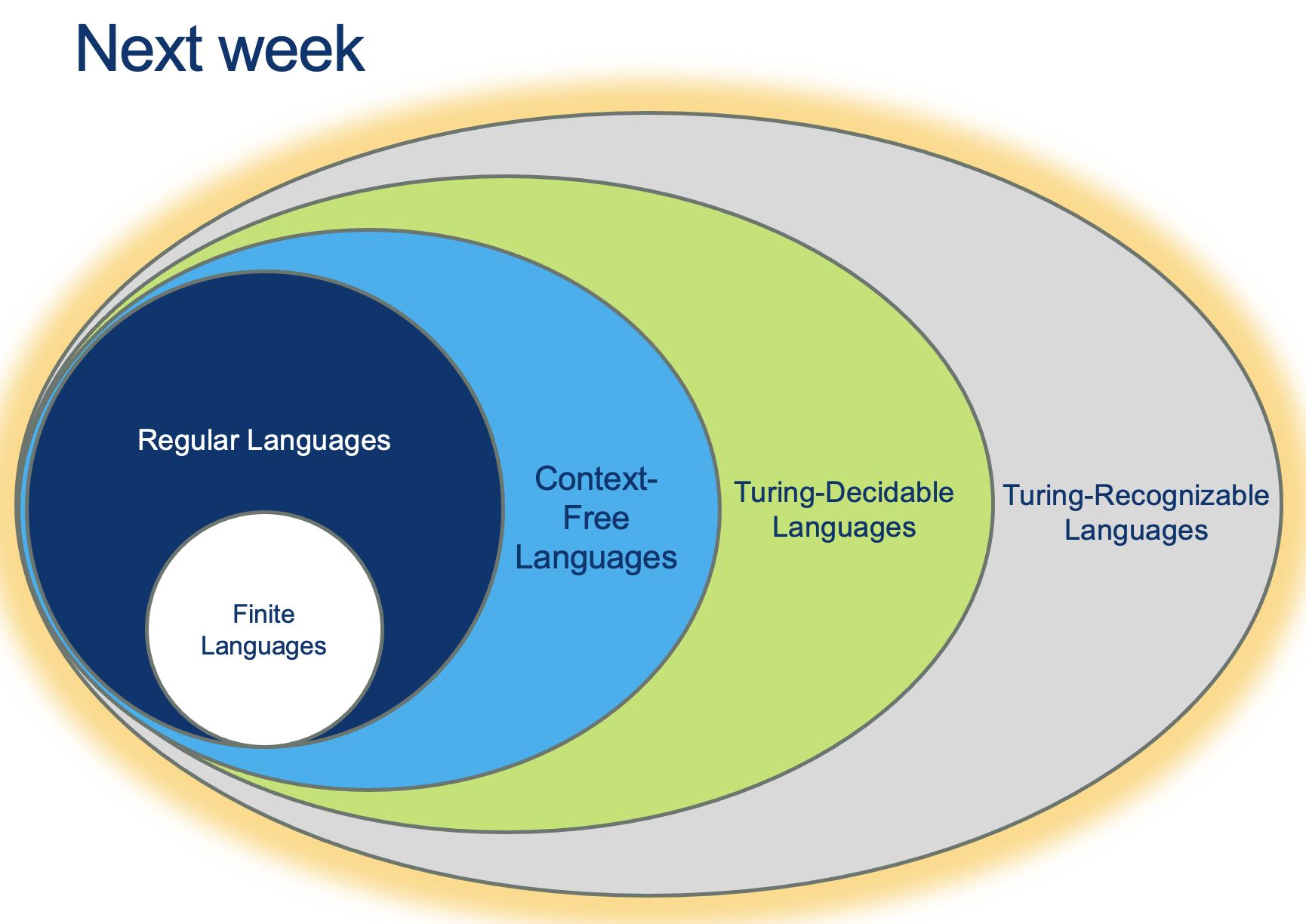
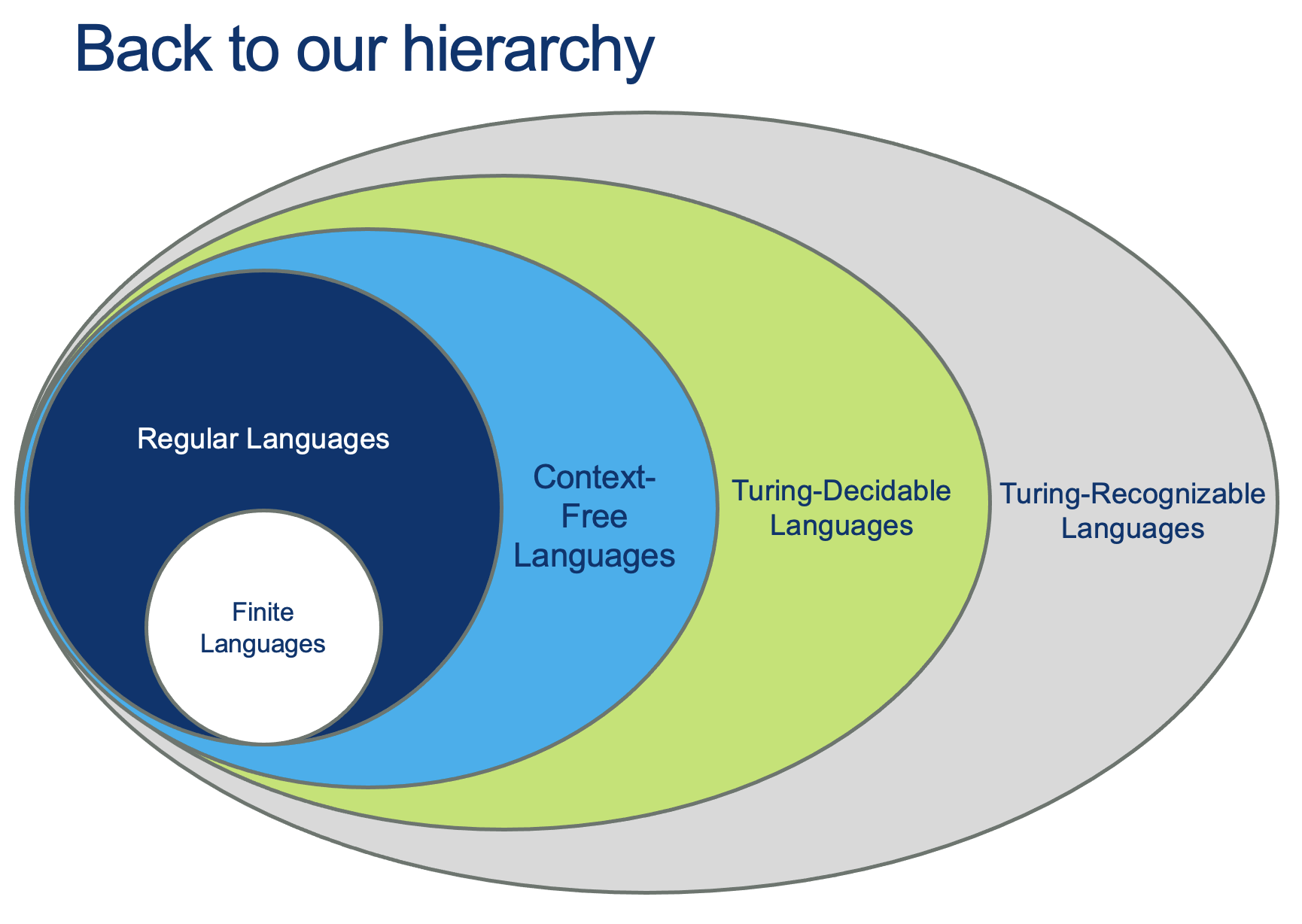
Recognizing vs Deciding
Recognizing a word is having the capacity of saying “YES, I know this one”, if that word is in the Language $L$ you are able to “Recognize”.
Note: If you are trying to Recognize a word, but you are not done checking, …. how long do you wait?
In other words, you just say: If I say “YES”, I’m sure it is “YES” (ACCEPT), but I don’t promise anything else.
Deciding a word is having the capacity of saying “YES, I know this one”, if that word is in the Language $L$ you are able to “Decide”, AND “NO, this one is NOT one of mine” for ALL words that are not in the Language you are able to “Decide” (called the complement of $L$, or $L^c$ or $\bar{L}$.
Examples
A Decider for PAL

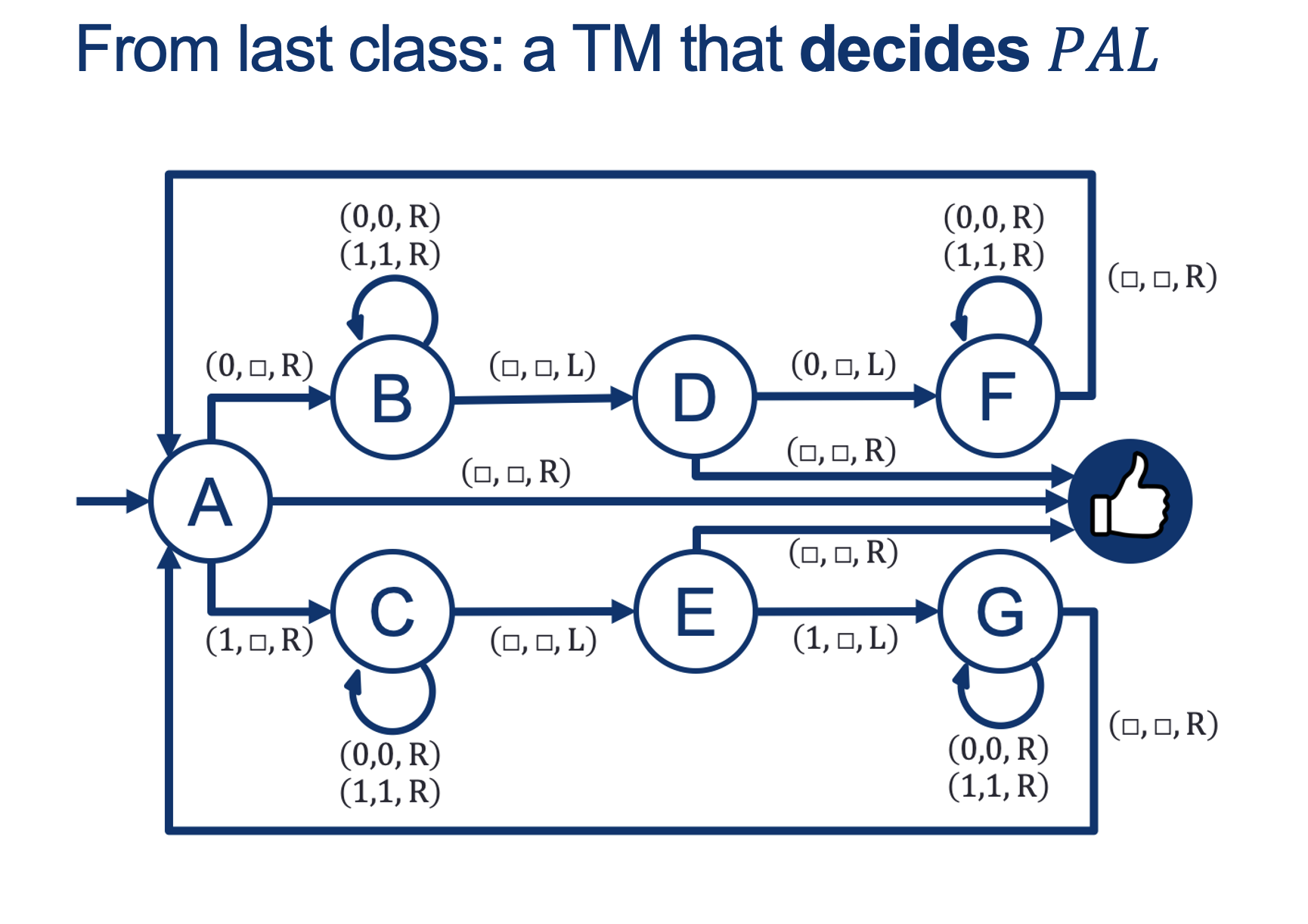

On input w:
while there are symbols left in the tape:
i. note whether 1st letter is a 0 or a 1 and erase it
ii. go all the way to the last symbol
iii. if this symbol doesn't match the one we just erased, REJECT;
otherwise erase it and go back to the start.
ACCEPT.
Recap: A Decider for HALT?
if we define HALT as:
\[\{ w \vert w = < M, \hat{w}> \text{ where M is a TM and M HALTS on } \hat{w} \}\]We can prove a Decider for HALT cannot exist by contradiction:
Suppose it exists:
\[\begin{align*} &M_{HALT}: \\ & \text{On INPUT $< M, \hat{w} >$} \\ & \quad \text{ if M HALTS on $\hat{w}$, ACCEPT } \\ & \quad \text{ if M FLOOPS on $\hat{w}$, REJECT } \end{align*}\]If we build the helper machine $M_X$:
\[\begin{align*} &M_X: \\ & On \; INPUT \; < M > \\ & \quad \text{Make } \hat{w} = < M > \color{gray}{ \text{# a copy of the input machine's description} }\\ & \quad \text{run $M_{HALT} ( < M , \hat{w}>)$} \quad \color{gray}{ \text{# run $M_{HALT} ( < M , < M > > )$ } } \\ & \quad \text{if $M_{HALT}( < M , \hat{w} > )$ returns ACCEPT, FLOOP on purpose } \\ & \quad \text{if $M_{HALT}( < M , \hat{w} > )$ returns REJECT, ACCEPT } \\ \end{align*}\]And run $M_X$ with input equal to itself, we get:
\[\begin{align*} &M_X: \\ & On \; INPUT \; < M_x > \\ & \quad \text{run $M_{HALT} ( < M_x , M_x > )$}\\ & \quad \text{if $M_{HALT}( < M_x , M_x > )$ returns ACCEPT, FLOOP on purpose } \\ & \quad \text{if $M_{HALT}( < M_x , M_x > )$ returns REJECT, ACCEPT } \\ \end{align*}\]- This run of $M_X$ takes in the description of itself $< M_X >$ as input
-
It calls $M_{HALT}$ to check if it HALTS on its own description (remember that $M_{HALT}$ should always have a consistent answer!):
- If $M_{HALT}$ predicts that $M_{X}$ HALTS on its own description (ACCEPT), $M_X$ FLOOPS on purpose… But that means that we just FLOOPED when runing $M_{X}$ with its own input (which is exactly the opposite of what $M_{HALT}$ predicted!)
- If $M_{HALT}$ predicts that $M_{X}$ FLOOPS on its own description (REJECT), $M_X$ ACCEPTS!… But that means that we just HALTED when runing $M_{X}$ with its own input (which is exactly the opposite of what $M_{HALT}$ predicted!)
A CONTRADICTION
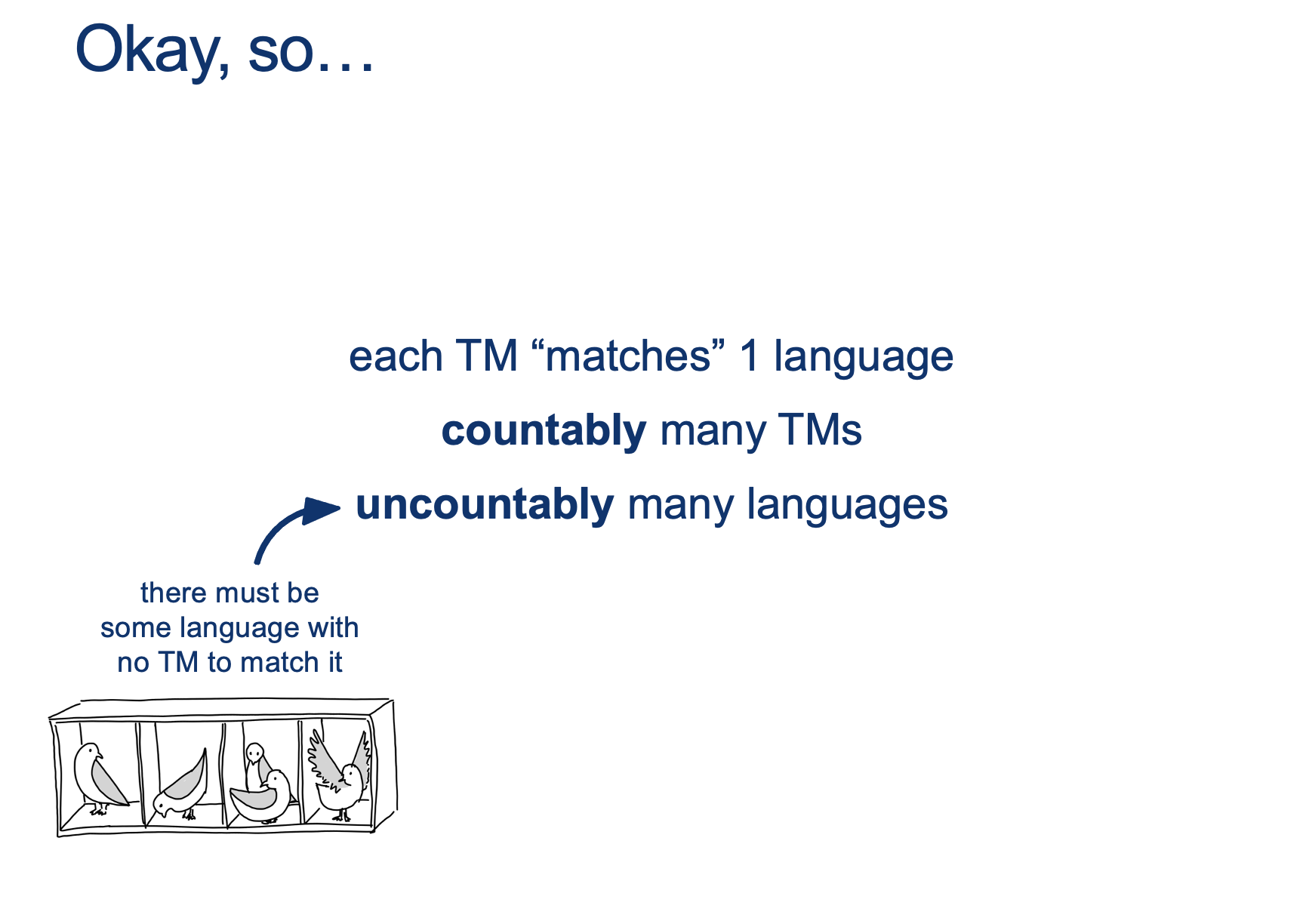
Since the ONLY assumption was that $M_{HALT}$ exists, then that means that $M_{HALT}$ cannot exist!


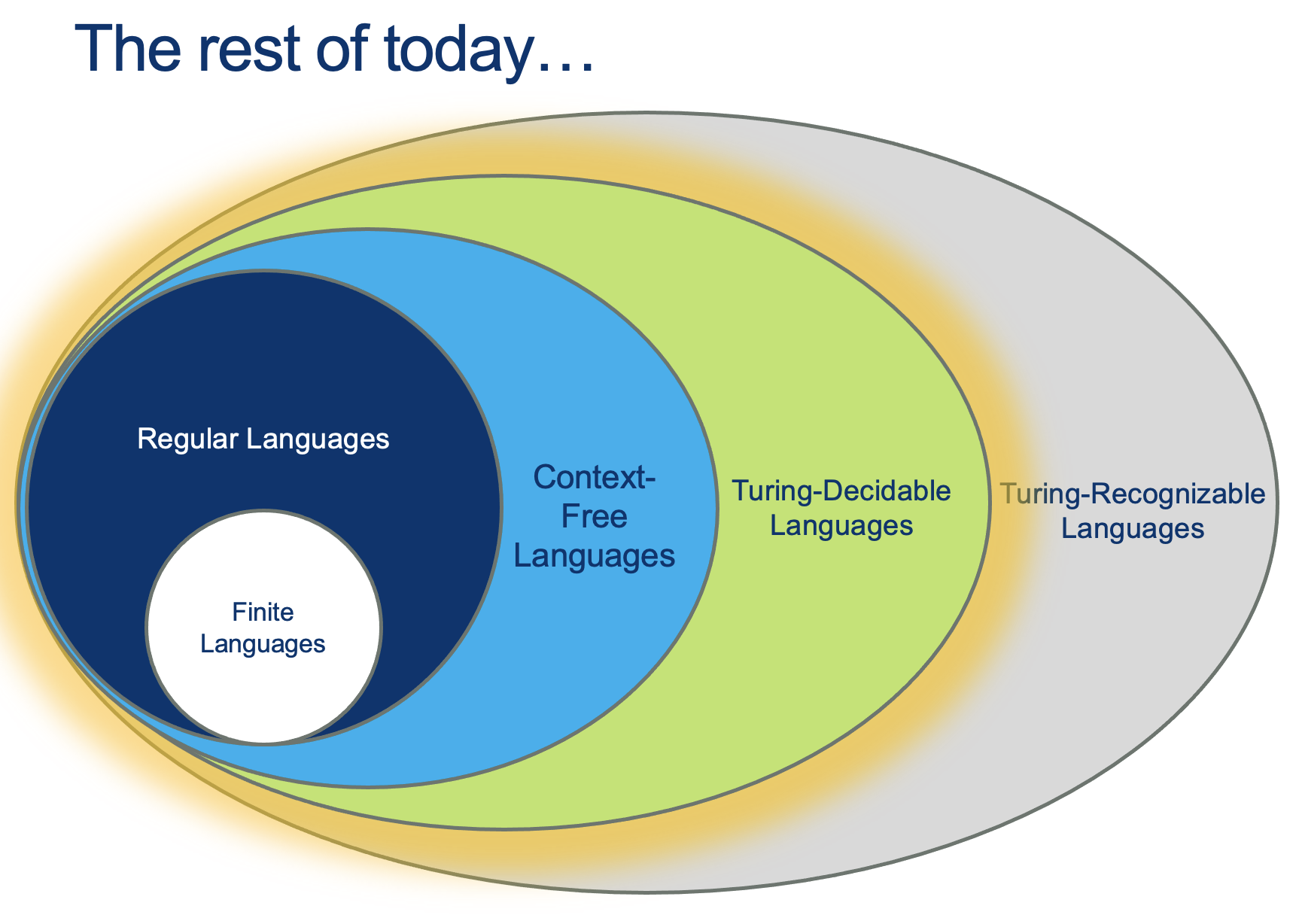


(Wait; then Click)
- Run both machines in parallel
- $\qquad$ Accept if either accepts

(Wait; then Click)
- Run both machines in parallel
- $\qquad$ Accept if both accept

(Wait; then Click)
- Suppose that M decides L.
- Design a new machine $M^\prime$ that behaves just like M, but:
- If M accepts, $M^{\prime}$ rejects
- If M rejects, $M^{\prime}$ accepts
- Formally, can do this by interchanging $q_{acc}$ and $ q_{rej}$
- Then $M^{\prime}$ decides $L^c$


(Wait; then Click)
- Run both M1 and M2 on w
- One must accept
-
- If M1 accepts, then M accepts
- If M 2 accepts, then M rejects
What can we do?
{: width="80%"}