Lecture Notes 17: Reductions

Outline

This class we’ll discuss:

Recap on TMs and Decidability vs Recognizability
ATM
Reductions

A Slideshow:

GUIDED NOTES (Optional)

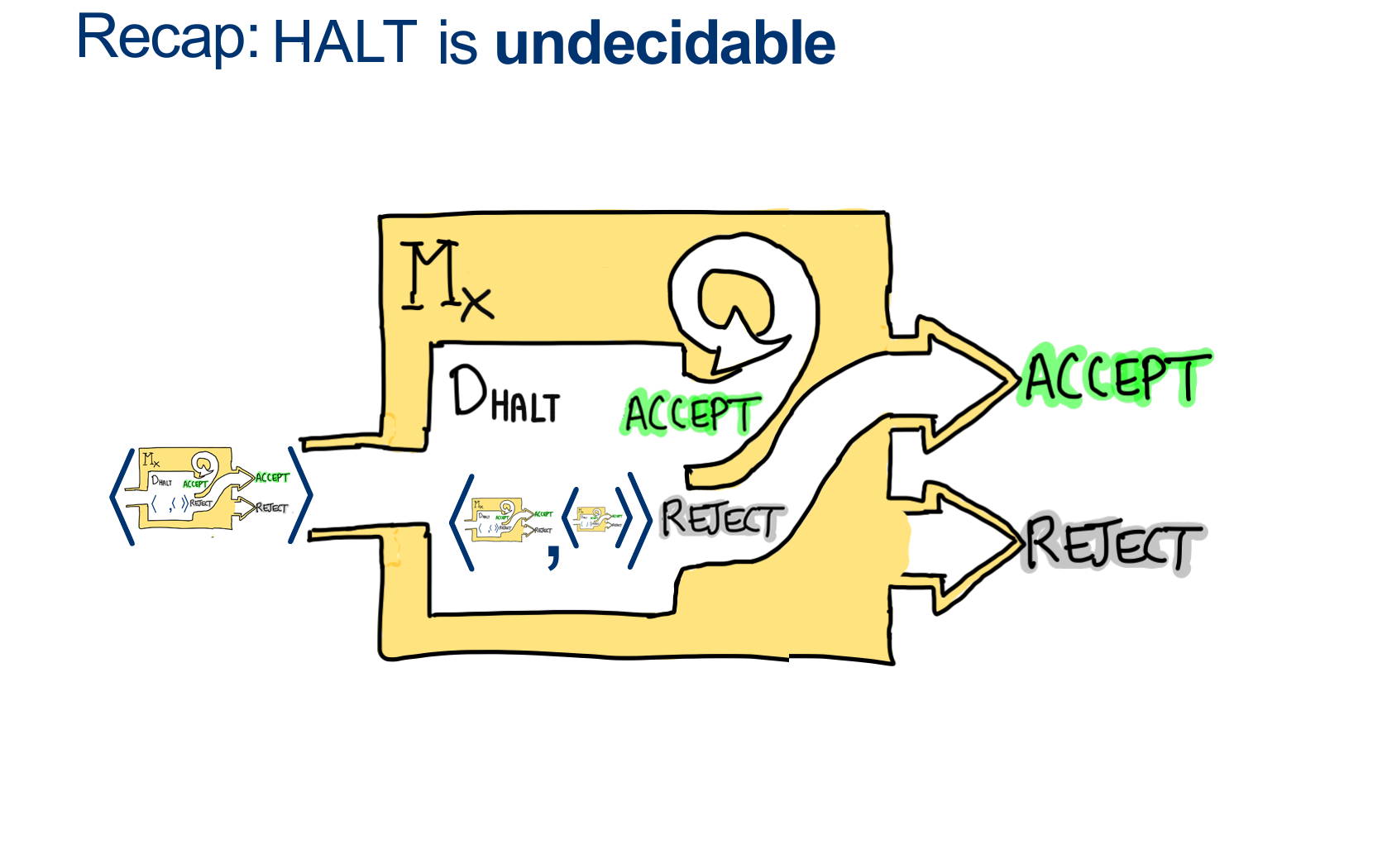
Recap: Two contradiction machines:

Contradiction Machine 1: $M_{X}$ to prove $D_{HALT}$ can’t exist:

Suppose $D_{HALT}$ exists and it always replies with a consistent answer:

\[\begin{align*} &M_{HALT}: \\ & \text{On INPUT $< M, \hat{w} >$} \\ & \quad \text{ if M HALTS on $\hat{w}$, ACCEPT } \\ & \quad \text{ if M FLOOPS on $\hat{w}$, REJECT } \end{align*}\]

If we build the helper machine $M_X$:

\[\begin{align*} &M_X: \\ & On \; INPUT \; < M > \\ & \quad \text{Make } \hat{w} = < M > \color{gray}{ \text{# a copy of the input machine's description} }\\ & \quad \text{run $M_{HALT} ( < M , \hat{w}>)$} \quad \color{gray}{ \text{# run $M_{HALT} ( < M , < M > > )$ } } \\ & \quad \text{if $M_{HALT}( < M , \hat{w} > )$ returns ACCEPT, FLOOP on purpose } \\ & \quad \text{if $M_{HALT}( < M , \hat{w} > )$ returns REJECT, ACCEPT } \\ \end{align*}\]

And run $M_X$ with input equal to itself, we get:

\[\begin{align*} &M_X: \\ & On \; INPUT \; < M_x > \\ & \quad \text{run $M_{HALT} ( < M_x , M_x > )$}\\ & \quad \text{if $M_{HALT}( < M_x , M_x > )$ returns ACCEPT, FLOOP on purpose } \\ & \quad \text{if $M_{HALT}( < M_x , M_x > )$ returns REJECT, ACCEPT } \\ \end{align*}\]

This causes an inconsistent response from $D_{HALT}$: a contradiction

therefore, $D_{HALT}$ can’t exist.

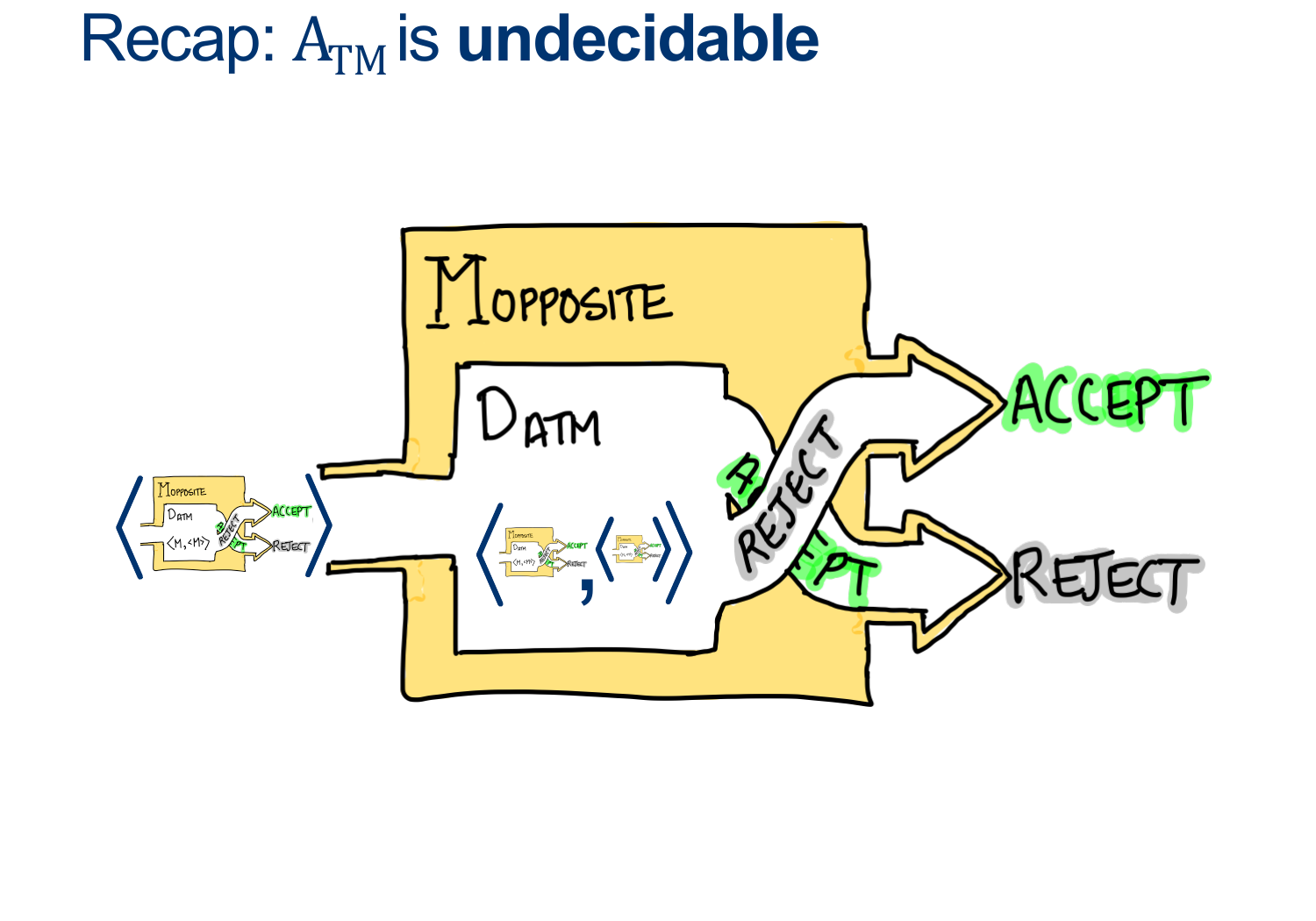
Contradiction Machine 2: $M_{OPPOSITE}$ to prove $D_{ATM}$ can’t exist:

Prove that the following Language is NOT Decidable:

\[ATM = \{ <M, w> \vert \text{ M is a TM that accepts the word w} \}\]

Step 1: Assume Is ATM is Decidable Now try to use this “fact” to arrive at a contradiction

Again, this means that $D_{ATM}$ exists and it always replies with a consistent answer.

Consider the Machine $M_{OPPOSITE} ( < M> )$

\[\begin{align*} &M_{OPPOSITE}:\\ & \quad \text{ On input $ < M > $ }:\\ & \quad \text{ Simulate $D_{ATM} \; on \; < M , < M > > $}\\ & \quad \text{ If $D_{ATM}$ accepts, REJECT. }\\ & \quad \text{ If $D_{ATM}$ rejects, ACCEPT. }\\ \end{align*}\]

And run $M_{OPPOSITE}$ with input equal to itself, we get:

\[\begin{align*} &M_{OPPOSITE}:\\ & \quad \text{ On input $ < M_{OPPOSITE} > $ }:\\ & \quad \text{ Simulate $D_{ATM} \; on \; < M_{OPPOSITE} , M_{OPPOSITE} > $}\\ & \quad \text{ If $D_{ATM}$ accepts, REJECT. }\\ & \quad \text{ If $D_{ATM}$ rejects, ACCEPT. }\\ \end{align*}\]

This causes an inconsistent response from $D_{ATM}$: a contradiction

therefore, $D_{ATM}$ can’t exist.

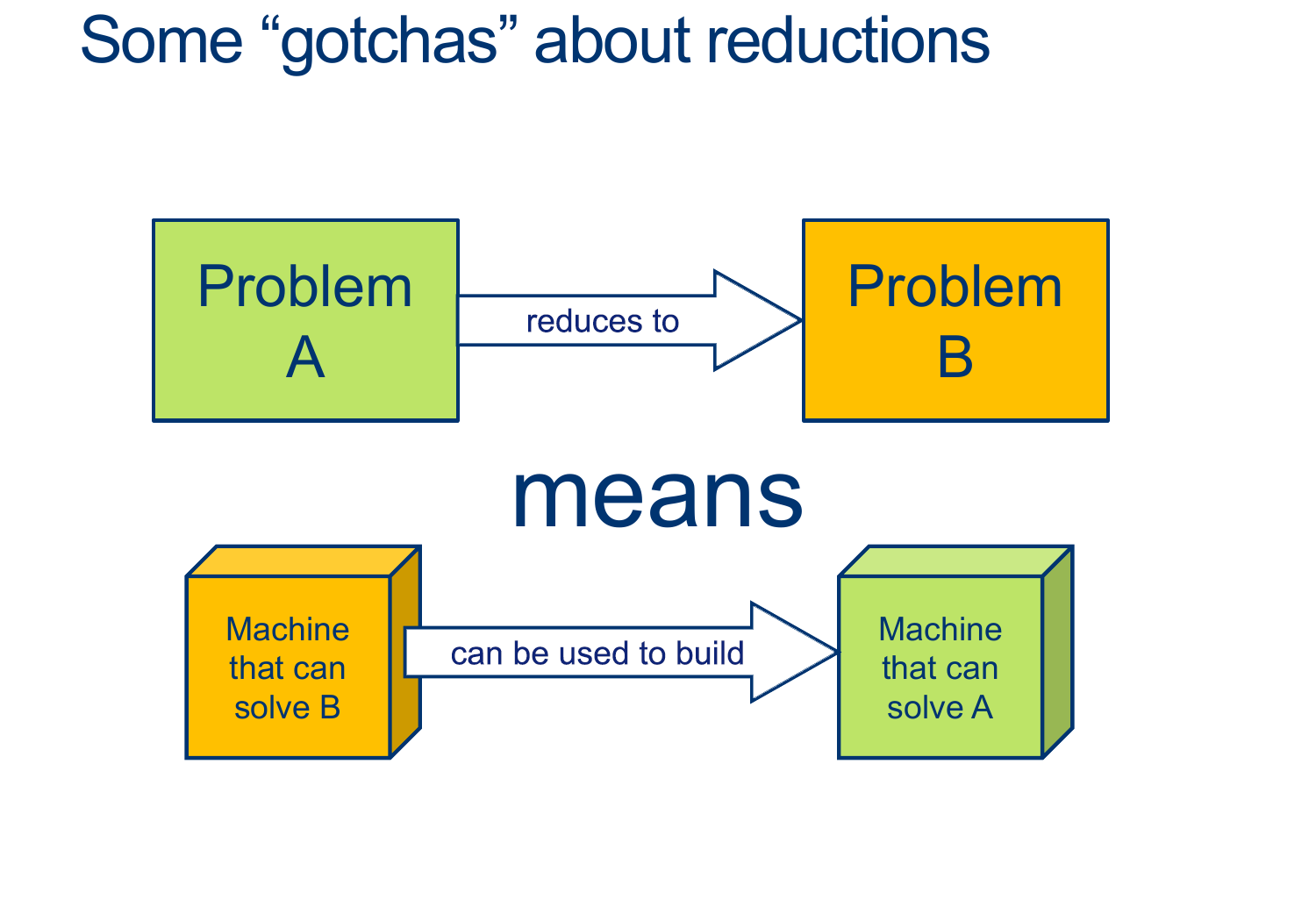
Contradiction Machines are hard… but there’s a better way

Let’s use the knowledge that ATM is undecidable to make a new proof that HALT is undecidable.

In other words, $ HALT$ is AT LEAST as hard as $ ATM $
(So if we can solve HALT, we can, for sure, solve ATM)

Try it out yourselves first

Think of a way you can get to say:
if we can solve HALT, we can, for sure, solve ATM

answer:

(Wait; then Click)

Assume HALT is decidable, and so there exists some $D_{HALT}$ that decides, for any input $< M,w>$, whether $M$ halts on $w$. We'll design the Machine $D_{ATM} $ as follows: $$ \begin{align*} &D_{ATM}:\\ & \text{ On input $ < M, w > $ }:\\ & \text{ Simulate $D_{HALT} \; on \; < M, w > $}\\ & \text{ If $D_{HALT}$ rejects, $M$ doesn't halt, so it did not accept: REJECT. }\\ & \text{ If $D_{HALT}$ accepts, we know $M$ won't loop forever, so }\\ & \quad \text{ Simulate $M$ on $w$ ADWID }\\ \end{align*} $$ This machine is a decider for ATM (why?)
– it avoided the only problem we had with solving ATM, namely telling the difference between looping and not waiting long enough.

However, we proved that ATM was undecidable by contradiction just a few minutes ago. Aaaand...the only condition we need to build $D_{ATM}$ was that $D_{HALT}$ existed, so ...

Since $D_{ATM}$ can't exist, $D_{HALT} \; $ must not exist.

Example:

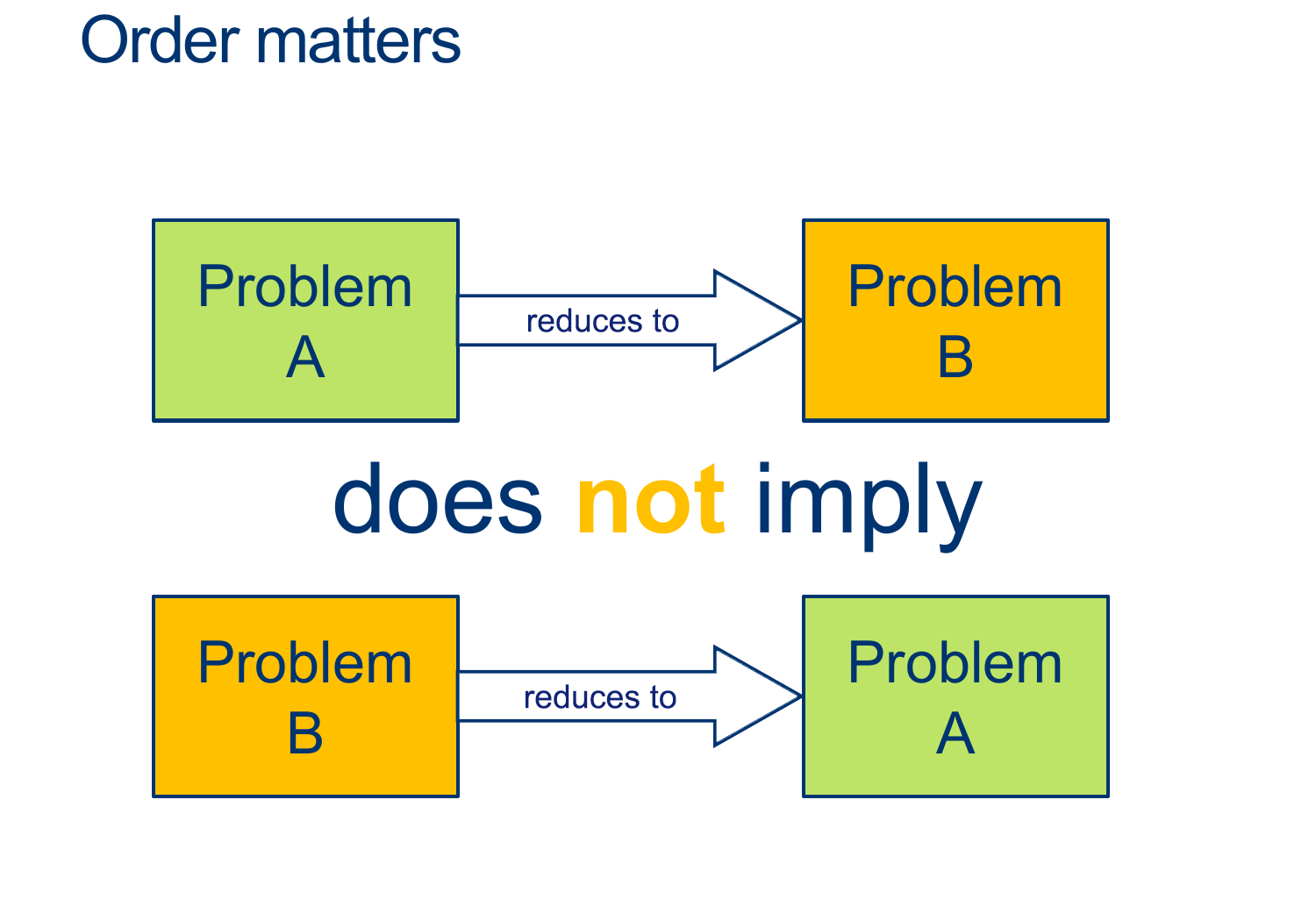
Above, we said:
$ ATM \leq HALT $

Therefore :

$D_{HALT}$ can be used to build $D_{ATM}$

Example:

Above, we said:
$ ATM \leq HALT $

Therefore :

It is possible that $D_{HALT}$ can be much harder to build than $D_{ATM}$, so if you have $D_{ATM}$, you would still have much more to do.
If you want to show equivalence, you have to prove both directions.

Let’s go together

Let’s try to say … “if we can solve ATM01, we can, for sure, solve ATM

answer:

(Wait; then Click)

Assume ATM01 is decidable, and so there exists some $D_{ATM01}$ that decides, for any input $< M >$, whether $M$ accepts $w = 01$. We'll design the Machine $D_{ATM} $ as follows: $$ \begin{align*} &D_{ATM}:\\ & \quad \text{ On input $ < M, w > $ }:\\ & \quad \text{ Simulate $D_{ATM01} \; on \; < M > $}\\ & \quad \text{ If $D_{ATM01}$ accepts, we know $M$ accepts string 01 }\\ & \quad \text{ If $D_{ATM01}$ rejects, we know $M$ doesn't accept string 01 }\\ & \quad \quad \text{ ... }\\ \end{align*} $$ Then what?
$D_{ATM01} $ only gives useful information about the string 01. It doesn't even look at the string $w$ (which we need to build $D_{ATM} $).
We’ll have the be a little more clever to get our machine to force it to check $w$.

Let’s go together

Let’s use, in addition to $D_{ATM01} $, an extra HELPER machine to help us extend the usefulness of $D_{ATM01} $.

answer:

(Wait; then Click)

Assume ATM01 is decidable, and so there exists some $D_{ATM01}$ that decides, for any input $< M >$, whether $M$ accepts $w = 01$. We'll design the Machine $D_{ATM} $ as follows: $$ \begin{align*} &D_{ATM}:\\ & \text{ On input $ < M, w > $ }:\\ & \text{ 1. build a HELPER machine (but don't run it yet) $Helper_{M,w}$ that is shown below: }\\ & \; \\ & \qquad Helper_{M,w}:\\ & \qquad \text{ On input $ x $ }: \quad \color{gray}{\text{# x: Anything! we don't care} }\\ & \qquad \text{ Ignore $ x $ and run $M$ on $w$ ADWID} \quad \color{gray}{\text{# We hardcode what $Helper_{M,w}$ does} }\\ & \; \\ & \text{ 2. Simulate $D_{ATM01}$ on $Helper_{M,w}$ } ADWID\\ \end{align*} $$ Analysis of cases What is going on?:

Inside our $D_{ATM} $ machine, we use $D_{ATM01} $ to ask if its input TM $M$ accepts $01$ ... But in order to do it ... it is forced to simulate the input machine $M$ ... instead of running $D_{ATM01} $ on $M$, we can have $D_{ATM01} $ run on a Trojan-Horse Machine whose only job is to check if $M$ accepts $w$!

$Helper_{M,w}$ is a TM built solely to check if the $M$ actually accepts the $w$ from the input to $D_{ATM} $ ($ < M, w > $ ).

When $D_{ATM01} $ runs $Helper_{M,w}$ with input $01$, we IGNORE the input and just run $M$ on $w$ It will actually answer if $M$ accepts $w$ rather than if the input $Helper_{M,w}$ accepts $01$.
- If $Helper_{M,w}$ replies ACCEPT, then $D_{ATM01}$ would return ACCEPT
- If $Helper_{M,w}$ replies REJECT, then $D_{ATM01}$ would return REJECT

The output of $D_{ATM01} $ is NOT actually answering if its input accepts $01$... it is secretly answering the question : "Does $M$ accept $w$?"

If $D_{ATM01} $ says that $Helper_{M,w}$ accepts 01, we know that $M$ must have accepted $w$.

For any $M, w$ pair that gets passed into $D_{ATM} $, we can construct a hardcoded helper machine and trick $D_{ATM01} $ into telling us the answer, in other words...deciding ATM.

However, This can't be true!!, we know ATM is undecidable, so ATM01 must also be undecidable.

Now, let’s try it again!

Prove that the following Language is NOT Decidable:

\[ATM11 = \{ <M> \vert \text{ M is a TM that accepts the word 11} \}\]