Lecture Notes 18: Undecidability and Reductions

Outline

This class we'll discuss:

• Intro to Undecidability
• Intro to Reductions

---

Recap: Decidability

Note: this is in PS05 so watch the vdeo recording to hear about how to solve this. (you should be able to clearly explain both approaches)

Recap: How about ATM?

Is ATM decidable?



Discuss if you could build \(D_L\) for the following language:
\[ A_{TM} = \{ < M, w> | \text{TM $M$ accepts } w \} \]

Can a \(D_{ATM}\) be constructed such that:

1. It Accepts any \(w \) such that \(w \in A_{TM}\)

AND


2. It Rejects any \(w \) such that \(w \notin A_{TM}\)

(Wait; then Click)

Intuition...Not decidable:

we can’t tell the difference between looping and “just haven’t waited long enough”.

But we can't prove "we haven't waited long enough" for each input... (AND we have infinite inputs)

But we can use another technique to try to prove this... CONTRADICTION!

If we can find a single example where we can't predict what \(D_{ATM}\) will say ... then we have it!

Step 1: Assume Is ATM is Decidable Now try to use this "fact" to arrive at a contradiction


Consider the Machine \(M_{OPPOSITE} ( < M> )\)

\[ \begin{align*} &M_{OPPOSITE}:\\ & \text{ On input $ < M > $ }:\\ & \text{ Simulate $D_{ATM} \; on \; < M , < M > > $}\\ & \text{ If $D_{ATM}$ accepts, REJECT. }\\ & \text{ If $D_{ATM}$ rejects, ACCEPT. }\\ \end{align*} \]



















In other words, \( HALT\) is AT LEAST as hard as \( ATM \)
(So if we can solve HALT, we can, for sure, solve ATM)







Try it out yourselves first

Think of a way you can get to say:
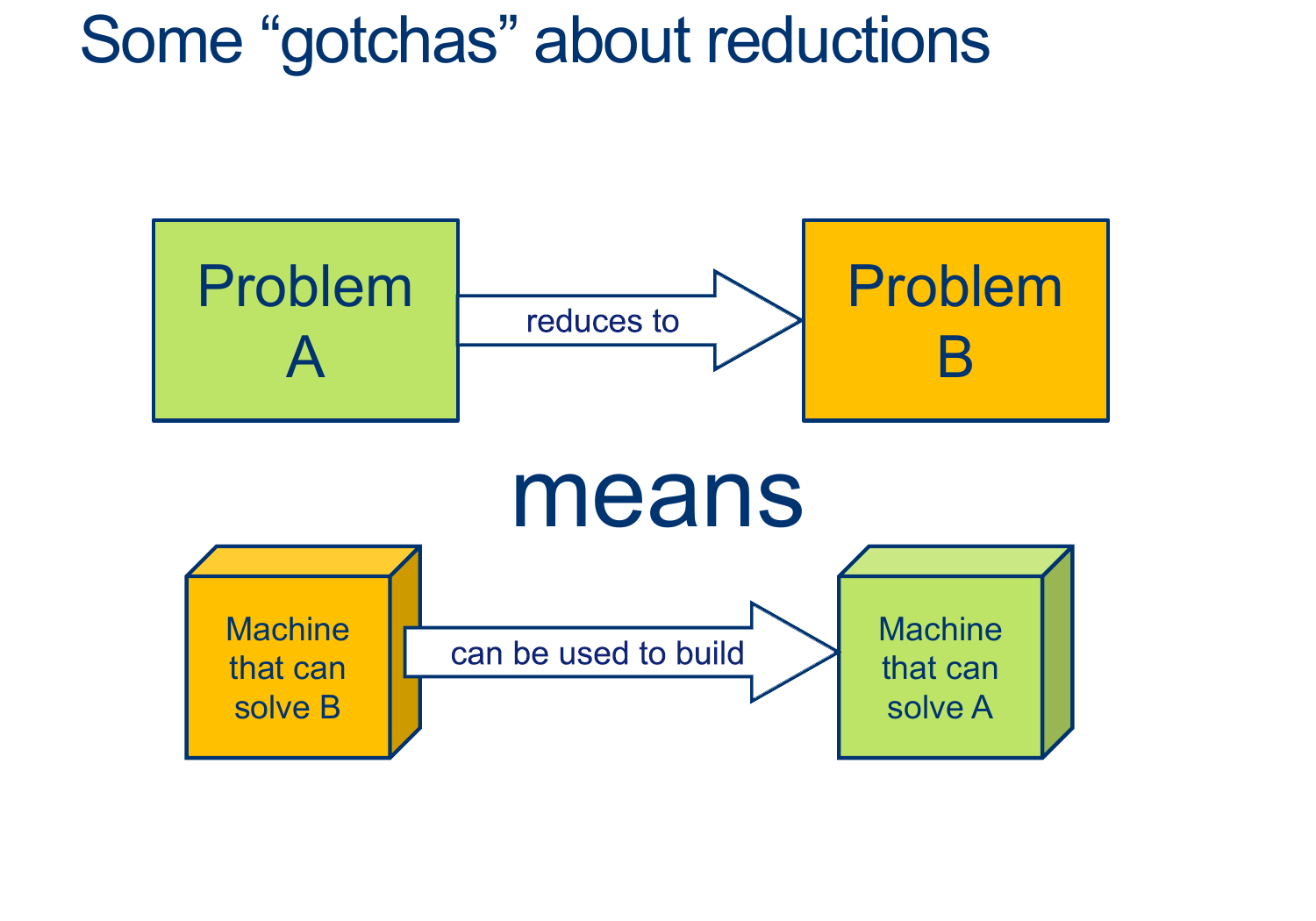
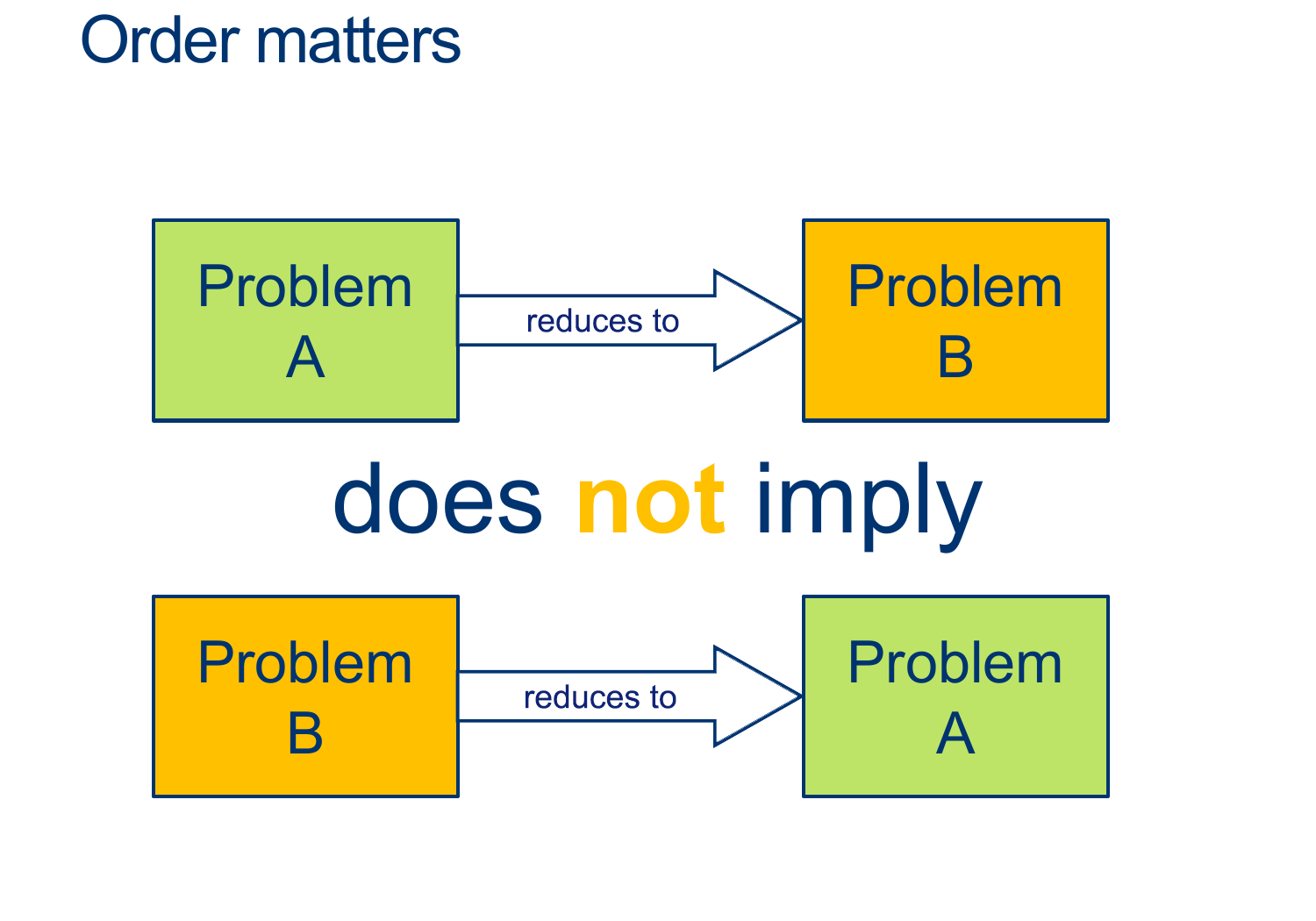
if we can solve HALT, we can, for sure, solve ATM

(Wait; then Click)

Assume HALT is decidable, and so there exists some \(D_{HALT}\) that decides, for any input \(< M,w>\), whether \(M\) halts on \(w\).

We'll design the Machine \(D_{ATM} \) as follows:

\[ \begin{align*} &D_{ATM}:\\ & \text{ On input $ < M, w > $ }:\\ & \text{ Simulate $D_{HALT} \; on \; < M, w > $}\\ & \text{ If $D_{HALT}$ rejects, $M$ doesn't halt, so it did not accept: REJECT. }\\ & \text{ If $D_{HALT}$ accepts, we know $M$ won't loop forever, so }\\ & \quad \text{ Simulate $M$ on $w$ ADWID }\\ \end{align*} \]

This machine is a decider for ATM (why?)
– it avoided the only problem we had with solving ATM, namely telling the difference between looping and lot waiting long enough.

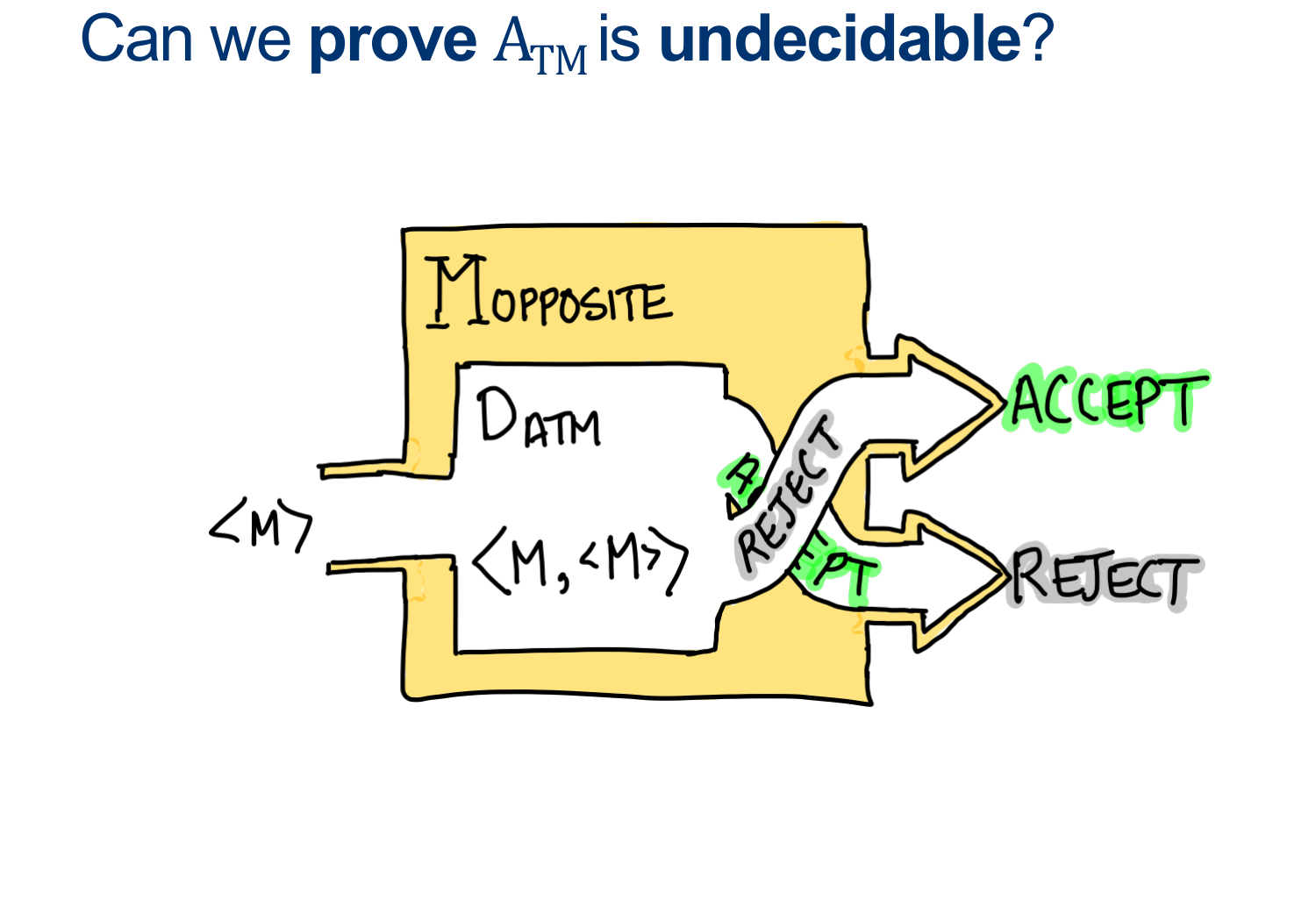
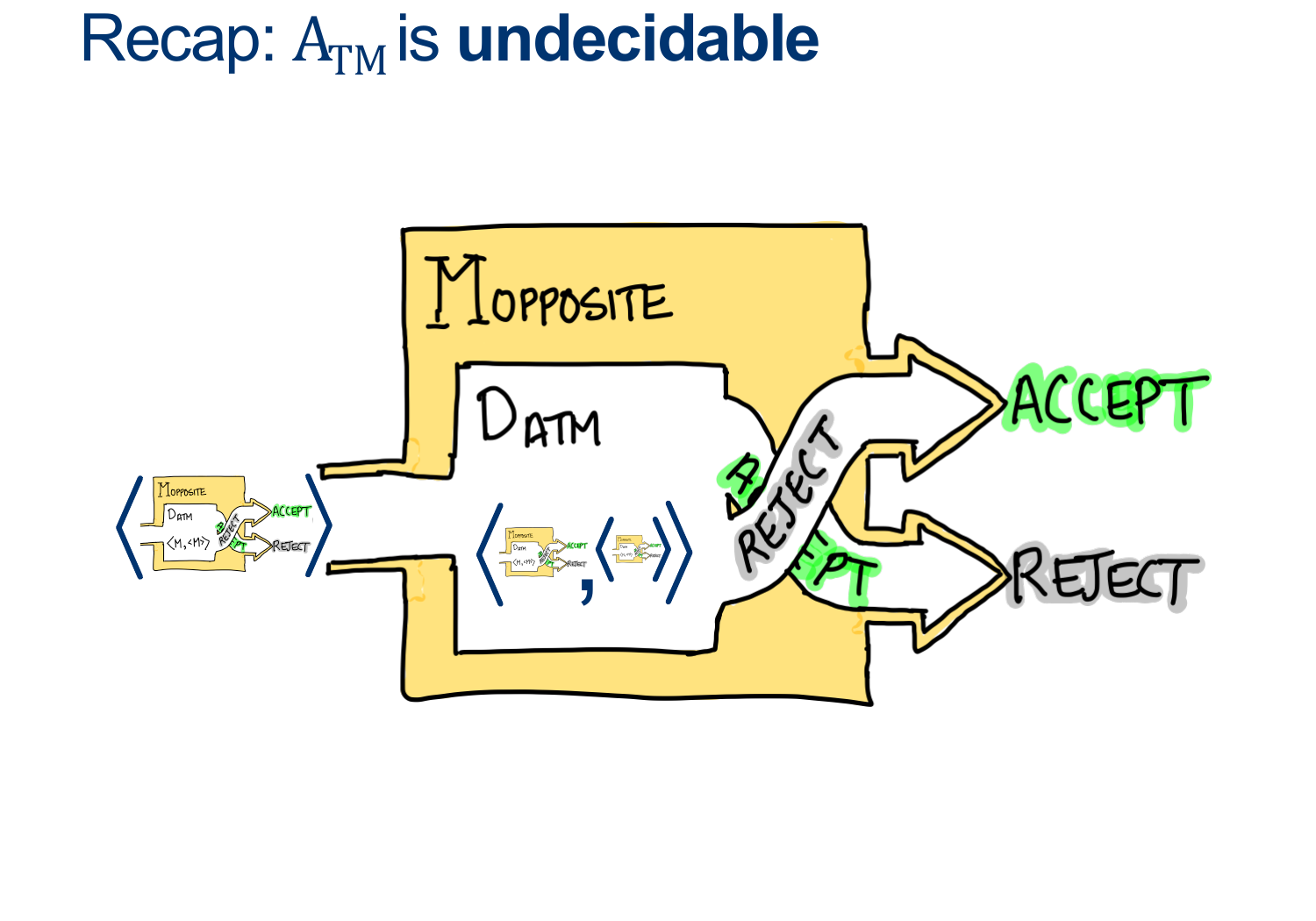
However, we proved that ATM was undecidable by contradiction just a few minutes ago.
Aaaand...the only condition we need to build \(D_{ATM}\) was that \(D_{HALT}\) existed, so ...
\(D_{HALT} \; \) must not exist.

Example:

Above, we said:
\( ATM \leq HALT \)

Therefore :

1. \(D_{HALT}\) can be used to build \(D_{ATM}\)

Example:

Above, we said:
\( ATM \leq HALT \)

Therefore :

• It is possible that \(D_{HALT}\) can be much harder to build than \(D_{ATM}\), so if you have \(D_{ATM}\), you would still have much more to do.



• If you want to show equivalence, you have to prove both directions.

Let's go together

Let's try to say ... "if we can solve ATM01, we can, for sure, solve ATM

(Wait; then Click)

Assume ATM01 is decidable, and so there exists some \(D_{ATM01}\) that decides, for any input \(< M >\), whether \(M\) accepts \(w = 01\).

We'll design the Machine \(D_{ATM} \) as follows:

\[ \begin{align*} &D_{ATM}:\\ & \text{ On input $ < M, w > $ }:\\ & \text{ Simulate $D_{ATM01} \; on \; < M > $}\\ & \text{ If $D_{ATM01}$ accepts, we know $M$ accepts string 01 }\\ & \text{ If $D_{ATM01}$ rejects, we know $M$ doesn't accept string 01 }\\ & \quad \text{ ... }\\ \end{align*} \]

Then what?
\(D_{ATM01} \) only gives useful information about the string 01.
It doesn't even look at the string \(w\) (which we need to build \(D_{ATM} \)).

We’ll have the be a little more clever to get our machine to force it to check \(w\).

Let's go together

Let's use, in addition to \(D_{ATM01} \), an extra HELPER machine to help us extend the usefulness of \(D_{ATM01} \).

(Wait; then Click)

Assume ATM01 is decidable, and so there exists some \(D_{ATM01}\) that decides, for any input \(< M >\), whether \(M\) accepts \(w = 01\).

We'll design the Machine \(D_{ATM} \) as follows:

\[ \begin{align*} &D_{ATM}:\\ & \text{ On input $ < M, w > $ }:\\ & \text{ 1. build a HELPER machine (but don't run it yet) $Helper_{M,w}$ that is shown below: }\\ & \; \\ & \qquad Helper_{M,w}:\\ & \qquad \text{ On input $ x $ }: \quad \color{gray}{\text{# x: Anything! we don't care} }\\ & \qquad \text{ Ignore $ x $ and run $M$ on $w$ ADWID} \quad \color{gray}{\text{# We hardcode what $Helper_{M,w}$ does} }\\ & \; \\ & \text{ 2. Simulate $D_{ATM01}$ on $Helper_{M,w}$ } ADWID\\ \end{align*} \]



Analysis of cases

What is going on?:

• Inside our \(D_{ATM} \) machine, we use \(D_{ATM01} \) to ask if its input TM \(M\) accepts \(01\) ...
  But in order to do it ... it is forced to simulate the input machine \(M\) ... instead of running \(D_{ATM01} \) on \(M\), we can have \(D_{ATM01} \) run on a Trojan-Horse Machine whose only job is to check if \(M\) accepts \(w\)!
• \(Helper_{M,w}\) is a TM built solely to check if the \(M\) actually accepts the \(w\) from the input to \(D_{ATM} \) (\( < M, w > \) ).


• When \(D_{ATM01} \) runs \(Helper_{M,w}\) with input \(01\), we IGNORE the input and just run \(M\) on \(w\)
  It will actually answer if \(M\) accepts \(w\) rather than if the input \(Helper_{M,w}\) accepts \(01\).
  1. If \(Helper_{M,w}\) replies ACCEPT, then \(D_{ATM01}\) would return ACCEPT
  2. If \(Helper_{M,w}\) replies REJECT, then \(D_{ATM01}\) would return REJECT


• The output of \(D_{ATM01} \) is NOT actually answering if its input accepts \(01\)... it is secretly answering the question : "Does \(M\) accept \(w\)?"

If \(D_{ATM01} \) says that \(Helper_{M,w}\) accepts 01,
we know that \(M\) must have accepted \(w\).

For any \(M, w\) pair that gets passed into \(D_{ATM} \), we can construct a hardcoded helper machine and trick \(D_{ATM01} \) into telling us the answer,
in other words...deciding ATM.

However, This can't be true!!,
we know ATM is undecidable, so ATM01 must also be undecidable.

---

Next class: More Reductions

---

Homework

[Due for everyone]

PS06 Due Next Friday

[Optional]

TODO