SmithLogo

CSC 250

Theory of Computation

Smith Computer Science



Lecture Notes 17: Decidability Vs Undecidability


Outline

This class we'll discuss:



Recap: Decidability











Closure of Decidable Languages

















(Wait; then Click)
  • Proof: \(\Rightarrow\)
    • Suppose that \(L\) is decidable.
    • Then \(L\) is recognizable
    • Also, \(L^c\) is decidable, and therefore recognizable.
  • Proof: \(\Leftarrow\)
    • Given M1 recognizing \(L\) , and M2 recognizing \(L^c\) .
    • Produce a Turing Machine M that decides whether or not its input w is in \(L\) or \(L^c\) .




    How so we build a Decider from M1 and M2?
    (Wait; then Click)

     Run both M1 and M2 on w.
    • One must accept.
    • If M1 accepts, then M accepts.
    • If M2 accepts, then M rejects.

    How? In sequence? What if M1 floops?
    What can we do?




    How do we deal with Floops?
    (Wait; then Click)











    Countable Vs Uncountable

    A Countable set is one that has a 1-to-1 correspondence with the natural numbers \(\mathcal{N}\).
    An Uncountable set is one where there is no such correspondence

    See "THE DIAGONALIZATION METHOD" in Sipser, 3rd Ed. P 202.

    Example: Use the Diagonalization method to prove \( R \) is uncountable.







    Note: (imagine a list of all valid Turing machines sorted alphabetically and by size)



    Thought 2



    • An infinite binary sequence is an unending sequence of 0s and 1s
    • Observe that the set \(\mathcal{B}\) of all infinite binary sequences is uncountable
      (we could not "line them up" with \(\mathcal{N}\) ... Use the Diagonalization method to prove it!)
    • Let \(\mathcal{L}\) be the set of all languages over alphabet \(\Sigma\). There is a correspondence between \(\mathcal{L}\) and the set \(\mathcal{B}\).
    • Therefore, the set of all languages over alphabet \(\Sigma\), \(\mathcal{L}\) is uncountable


    • Each TM \( M_i \) matches to a single language \( L_i \) from \(\mathcal{L}\) (for a given \(\Sigma\) ) so we have countably many Turing-Recognizable Languages, but uncountably many languages in \(\mathcal{L}\) ...
      What does that mean?





    Intro to Undecidable Problems (Languages)




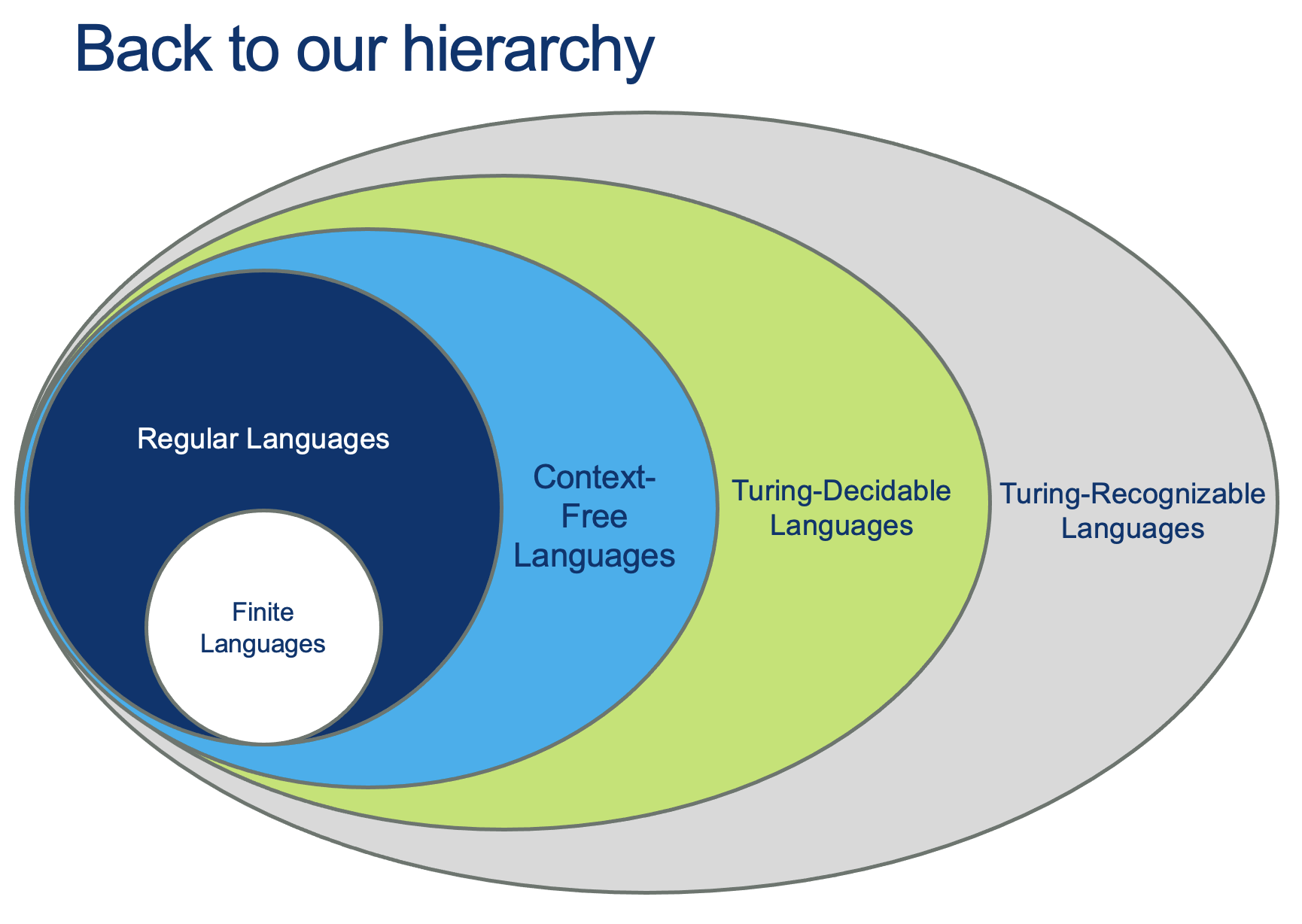
    Problems as Languages



    In this class, we have converted "finding a solution to a problem" to "Learning to accept words from a Language".

    In our world, Answering a question means building a machine that recognizes the language-version of that question.

    Example problem:
    "Can you come up with a binary string with a pattern of 0s and 1s such that the string is a palindrome"

    Example Language-Version:
    \[ L = \{ w \in \Sigma^* | w^R = w \} \]

    Example solution:
    (See the CMF, PDA, or TM solutions to this problem)




    Questions about Machines



    Often we'll ask questions about the machines we've seen so far.

    Again, answering a question means building a machine that recognizes the language-version of that question.



    So, a problem like:
    "Find the set of Turing Machines that have up to 5 states",
    can be rephrased as finding the Language:
    \[ L = \{ < M > | M \text{ is a TM and } M \text{ has fewer than 5 states} \} \]




    Answering with an Algorithm



    How would you "Solve" the problem for:
    \[ L = \{ < M > | M \text{ is a TM and } M \text{ has fewer than 5 states} \} \]

    What could you use to "Solve" (Decide/Recognize) \(L\)?
    (Wait; then Click)

     Another Turing Machine!! ... A Decider for \(L\) we'll call \(D_L\)

    \[ \begin{align*} & D_L :\\ & \text{On INPUT } < M >\\ & \quad \text{Inspect the description of } M \\ & \quad \quad \text{IF $M$ is not a valid TM: REJECT} \\ & \quad \quad \text{ELSE IF $M$ has fewer than 5 states: ACCEPT} \\ & \quad \quad \text{ELSE: REJECT} \\ \end{align*} \]

    CAN we get stuck on a loop?
    (Note that we know something about description \(M\) that helps us answer this question)





    Questions about Machines



    Discuss if you could build \(D_L\) for the following language:
    \[ L = \{ < M, w > | TM M \text{ accepts } w \text{ in fewer than 10 steps} \} \]




    Questions about Machines



    Discuss if you could build \(D_L\) for the following language:
    \[ L = \{ < A > | \text{DFA $A$ accepts an infinite number of words (L(A) is infinite)} \} \]




    Questions about Machines



    Discuss if you could build \(D_L\) for the following language:
    \[ A_{TM} = \{ < M, w> | \text{TM $M$ accepts } w \} \]






    (Wait; then Click)

     Can we prove it is at least recognizable?

    Can we prove it is NOT Decidable?

    Are these two things the same?



    Next class: Reductions



    Homework


    [Due for everyone]
    TODO

    [Optional]
    TODO