CSC 250
Theory of Computation
Smith Computer Science
Theory of Computation
Smith Computer Science



# ------------------------------------------------------ # Example of how a Turing Machine (program) can create an # ad-hoc helper TM (program) to complete a reduction # in this case ATM ≤ ATM_01 # # By Pablo Frank Bolton # 2022 # ------------------------------------------------------ import sys from io import StringIO # Later, change to True for manual input manual_input = True def main(): '''Tests how example 'Deciders' This program has three main sections. In the first part, each individual function is tested directly with different strings. In the second part, the function D_ATM01 is used to test if an input function M accepts the string '01'. Three input functions M1, M2, and M3 are passed to D_ATM01 to demonstrate what it does. In the Third part, the 'Decider' function D_ATM is constructed around D_ATM01 and tested for various input pairs <M, w>. ''' print('M1, M2, M3 Testing STARTED') print('#############################') # Direct calls to M1, M2, and M3 with different words print ( f"Does M1 accept 01? :", end = "" ) print ( f" \t {M1('01')}" ) print ( f"Does M1 accept 11? :", end = "" ) print ( f" \t {M1('11')}" ) print ( f"Does M2 accept 01? :", end = "" ) print ( f" \t {M2('01')}" ) print ( f"Does M2 accept 11? :", end = "" ) print ( f" \t {M2('11')}" ) print ( f"Does M3 accept 01? :", end = "" ) print ( f" \t {M3('01')}" ) print ( f"Does M3 accept 0? :", end = "" ) print ( f" \t {M3('0')}" ) print('#############################') print('M1, M2, M3 Testing Done') print('\n') print('D_ATM_01 Testing STARTED') print('#############################') # Call to D_ATM01 to see if function M1 accepts '01' print ( f"Does M1 accept 01? :", end = "" ) print ( f" \t {D_ATM01(M1)}" ) # Call to D_ATM01 to see if function M2 accepts '01' print ( f"Does M2 accept 01? :", end = "" ) print ( f" \t {D_ATM01(M2)}" ) # Call to D_ATM01 to see if function M3 accepts '01' print ( f"Does M3 accept 01? :", end = "" ) print ( f" \t {D_ATM01(M3)}" ) print('#############################') print('D_ATM01 Testing Done') print('\n') print('D_ATM Testing STARTED') print('#############################') print ( f"Does M1 accept 010? :", end = "" ) print ( D_ATM(M1, '010') ) print() print ( f"Does M1 accept 000? :", end = "" ) print ( D_ATM(M1, '000') ) print() print ( f"Does M2 accept 11? :", end = "" ) print ( D_ATM(M2, '11') ) print() print ( f"Does M3 accept 111? :", end = "" ) print ( D_ATM(M3, '111') ) print() print ( f"Does M3 accept 010? :", end = "" ) print ( D_ATM(M3, '010') ) # enable manual input to test on M2 if manual_input: print('\n') word = input("Give a binary string or 'stop': ") while word != 'stop' or check_word(word): if word == 'stop': break if check_word(word): tm = input("choose a machine (1, 2, or default 3): ") if tm == "1": print ( D_ATM(M1, word) ) elif tm == "2": print ( D_ATM(M2, word) ) else: print ( D_ATM(M3, word) ) word = input("Give a binary string or 'stop': ") print('#############################') print('D_ATM Testing Done') def D_ATM01 ( M ): '''Checks if an input function M accepts string 01 ''' ret = M('01') if ret == True: return True elif ret == False: return False else: return '?' def M1(w:str): '''Accepts any string that starts with 01 ''' if len(w) >= 2: if w[0] == '0' and w[1] == '1': return True return False def M2(w:str): '''Accepts only string 11 ''' if len(w) == 2: if w[0] == '1' and w[1] == '1': return True return False def M3(w:str): '''Rejects any string shorter than 2 and Floops with any string of size 2 or greater ''' if len(w) >= 2: if w[0] == '0' and w[1] == '1': # Floop with artificial STOP max = 2 count = 0 while True: count+=1 if count > max: print ("\t ...I got impatient...", end = "" ) return '?' return True return False def D_ATM (M:str, w:str ): '''D_ATM is constructed using ONLY: A Helper is built specifically for the inputs M and w, which ignores any input given to it and simply runs M on w. D_ATM01 and ''' # a "string to run exec with" to make the Helper helper_def = f''' def Helper_{M.__name__}_{w}(x): # 0. ignore input x # 1. Simulate {M.__name__} on {w} # 2. ADWID print( {M.__name__}("{w}"), end = "" ) ''' # Creating the Helper for the specific M and w exec(helper_def) # a "string to run exec with" to call D_ATM01(Helper) D_ATM01_call = f"D_ATM01( Helper_{M.__name__}_{w} )" # create file-like string to capture output codeOut = StringIO() # capture output and errors sys.stdout = codeOut # Calling D_ATM01 with Helper as input exec(D_ATM01_call) # restore stdout and stderr sys.stdout = sys.__stdout__ #get the output from the called helper output = codeOut.getvalue() print(f"(Output from D_ATM01( Helper_{M.__name__}_{w} is {output}) ", end = "" ) codeOut.close() if output == 'True': return True elif output == 'False': return False else: return '?' def check_word(word): '''To check that strings are all 0s and 1s; for manual input''' char_list = ["0", "1"] matched_list = [chars in char_list for chars in word] if False in matched_list: return False return True if __name__ == "__main__": main()

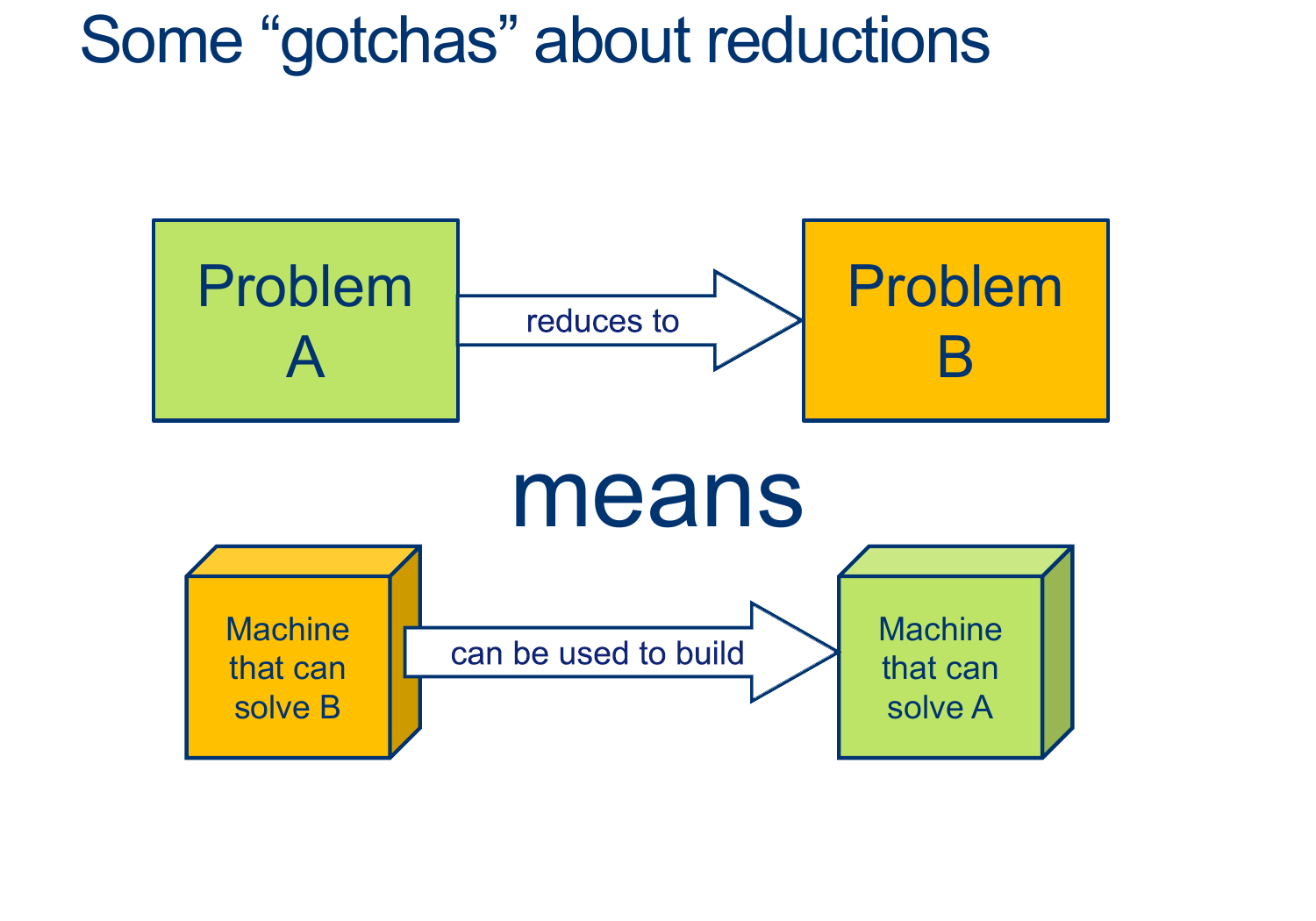
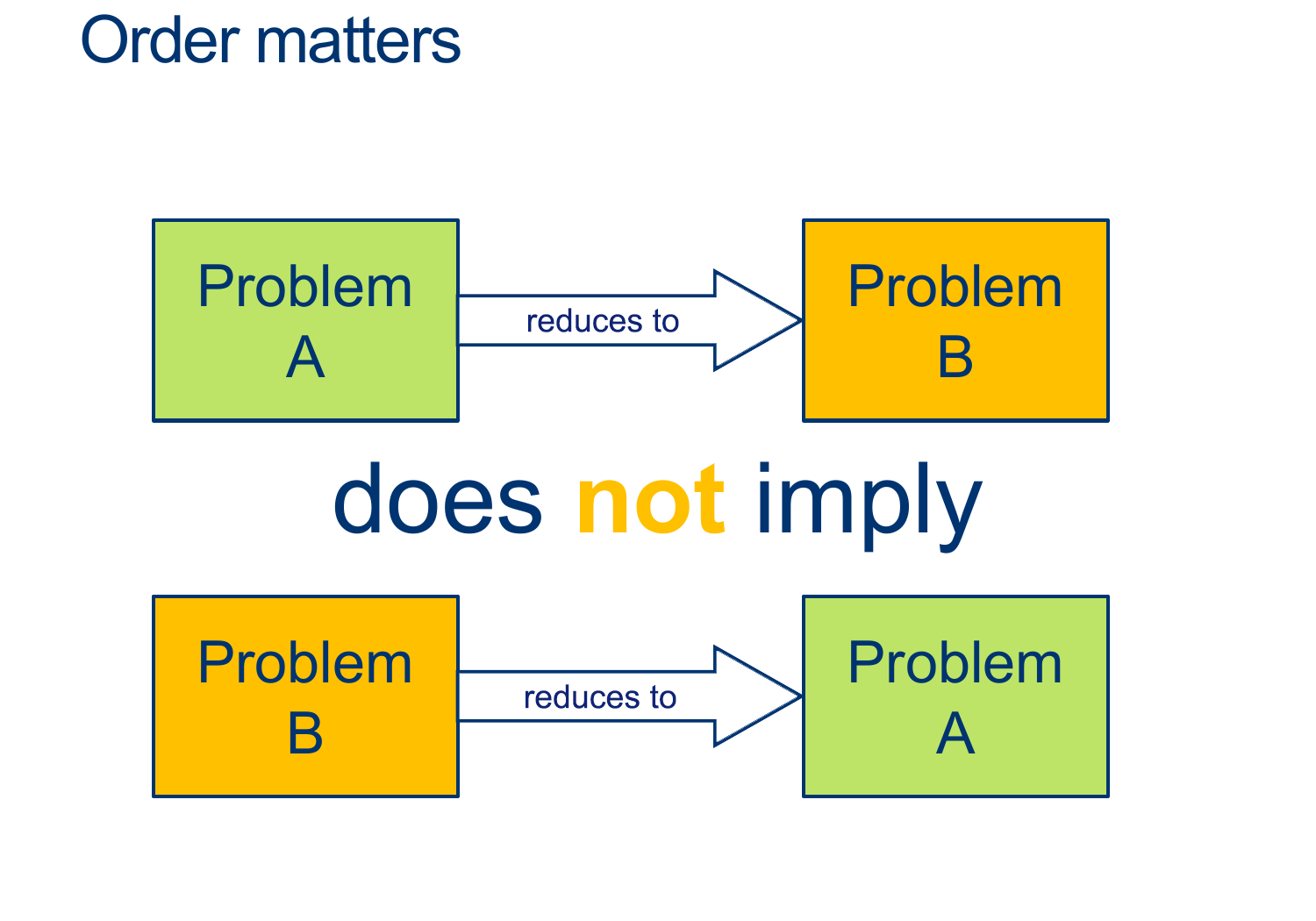
Let's go together
Let's use, in addition to \(D_{EMPTY} \), an extra HELPER machine to help us extend the usefulness of \(D_{EMPTY} \).
Is \(\overline{EMPTY}\) Decidable?
\(\overline{EMPTY}\) is the complement language of \(EMPTY\).
Its definition, should be:
\[ \overline{EMPTY} = \{ < M > | \text{TM $M$ accepts at least one string} \} \]
There is a first simple step: We can say, for sure that \(\overline{EMPTY}\) must be undecidable... Why?





NOTES: The Midterm will include everything UP to Turing Machines but NOT INCLUDING Reductions.