Lecture Notes 05:
Practice with Regular Expressions

Outline

This class we'll discuss:

• Overleaf check
• RE Recap
• Recap: RegEx (colorful example)
• RE Minigolf
• RE properties
• A simple RE proof

---

Overleaf and Latex

Typesetting is not required: legibly-written-and-then-Typed (Word/OpenOffice/etc) submissions are totally fine;
Just PDF them before you submit, please!

However, LaTeX (Latex henceforth) is a powerful tool that lets you tweak and customize ad nauseam, which might be desirable to some of you.
Also, it is the defacto standard for most academic publications.

If you choose Latex, you should start very simply; learn:

• Titles and Sections
• bold and Italics
• List Environments
• Math Environment and symbols

Activity 0 [10 minutes]:


For tips on how to write symbols and environments (like equations, lists, or tables),
You can check out this latex tutorial.

---

Definition of Regular Expressions (Recursively)

Basic (axiomatic) definitions:

• Basis 1: \(\emptyset\) is a regular expression, and \( \mathrm{L} (\emptyset) = \emptyset\)
• Basis 2: \(\epsilon\) is a regular expression, and \( \mathrm{L} (\epsilon) = \{\epsilon\} \)
• Basis 3: \(a\) is a symbol, then \(a\) is a regular expression, and \( \mathrm{L} (a) = \{a\} \)

Recursive extensions:

• Alternation:
  One expression or another,
  If \(\mathrm{R}_1\) and \(\mathrm{R}_2\) are regular expressions,
  then \(\mathrm{R}_1 + \mathrm{R}_2\) is a regular expression,
  and \( \mathrm{L} (\mathrm{R}_1 + \mathrm{R}_2) = \mathrm{L} (\mathrm{R}_1) \cup \mathrm{L} (\mathrm{R}_2)\)
  
  Example:
  If \( R_1 = 0\) and \( R_2 = 1\),
  what is \( R_3 = R_1 + R_2\) ?
  

  Think before revealing the answer:

  (Wait; then Click)

  \(R_3 = 0 + 1\)

  
  what is \( \mathrm{L} (\mathrm{R}_1 + \mathrm{R}_2) \)?

  Think before revealing the answer:

  (Wait; then Click)

  \( \mathrm{L} (\mathrm{R}_3 ) = \{ 0, 1\} \)



• Concatenation:
  If \(\mathrm{R}_1\) and \(\mathrm{R}_2\) are regular expressions,
  then \(\mathrm{R}_1 \mathrm{R}_2\) is a regular expression,
  and \( \mathrm{L} (\mathrm{R}_1 \mathrm{R}_2) = \mathrm{L} (\mathrm{R}_1) \mathrm{L} (\mathrm{R}_2)\)
  
  Example:
  If \( R_3 = (0 + 1)\) and \( R_4 = 1\),
  what is \( R_5 = R_3 R_4\) ?
  

  Think before revealing the answer:

  (Wait; then Click)

  \(R_5 = (0 + 1)1\)

  
  what is \( \mathrm{L} (\mathrm{R}_3 \mathrm{R}_4) \)?

  Think before revealing the answer:

  (Wait; then Click)

  \( \mathrm{L} (\mathrm{R}_5 ) = \mathrm{L} ( \; (0 + 1)1 \; ) = \{ 01, 11\} \)



• Kleene star:
  If \(\mathrm{R}_1\) is a regular expression,
  then \(\mathrm{R}^*_1\) is a regular expression,
  and \( \mathrm{L} (\mathrm{R}_1^*) = \big( \mathrm{L} (\mathrm{R}_1) \big)^* \)
  
  Example:
  If \( R_5 = (0 + 1)1 \),
  what is \( R_5^*\) ?
  

  Think before revealing the answer:

  (Wait; then Click)

  \(R_5^* = ( \; (0 + 1)1 \; )^*\)

  
  what is \( \mathrm{L} (\mathrm{R}_5^*) \)?

  Think before revealing the answer:

  (Wait; then Click)

  \( \mathrm{L} (\mathrm{R}_5^* ) = \mathrm{L} ( \; ((0 + 1)1)^* \; ) = (\mathrm{L} ( \; (0 + 1)1 \;))^* = ( \; \{ 01, 11\} \; )^* \)
  \( = \{ \epsilon, \quad 01, \quad 11, \quad 0101, \quad 0111, \quad 1101, \quad 1111, \quad 010101, \quad \dots \} \)

Precedence rules are: do parenthesis first, then do star first, then concatenation, then union.

---

The RegEx Minigolf!

Activity 1 [5-10 minutes!!]:
Make teams of 2 or 3 and complete the following challenges.
Let me know when your team is done.

---

Properties of Regular Languages

The following properties are true about regular languages:

• Claim: Regular languages are closed under union
• Claim: Regular languages are closed under concatenation
• Claim: Regular languages are closed under intersection
• Claim: Regular languages are closed under complement
• Claim: Regular languages are closed under difference
• Claim: Regular languages are closed under reversal

First Question: What does "Closed Under" mean?
In other words: What are closure properties?

We won't prove them (all) yet, but you may use them in Problem Set 2.

The meaning of the claims...

Now, what it is that the other claims are actually "claiming"?

(How would you express this in the notation we've developped so far?)

1. Claim: Regular languages are closed under union
   Think before revealing the answer:
   

   (Wait; then Click)

   For any regular languages \(L_1\) and \(L_2\), then \(L_1\cup L_2\) is regular



2. Claim: Regular languages are closed under concatenation
   Think before revealing the answer:
   

   (Wait; then Click)

   For any regular languages \(L_1\) and \(L_2\), then \(L_1L_2\) is regular



3. Claim: Regular languages are closed under intersection
   Think before revealing the answer:
   

   (Wait; then Click)

   For any regular languages \(L_1\) and \(L_2\), then \(L_1 \cap L_2\) is regular



4. Claim: Regular languages are closed under complement
   Think before revealing the answer:
   

   (Wait; then Click)

   For regular language \(L_1\), \( (L_1)^c \) is regular



5. Claim: Regular languages are closed under difference
   Think before revealing the answer:
   

   (Wait; then Click)

   For any regular languages \(L_1\) and \(L_2\), then \(L_1 - L_2\) is regular
   this can also be written as: \(L_1 \setminus L_2\)



6. Claim: Regular languages are closed under reversal
   The reversal of a string \(a_1a_2 \dots a_n\) is the string written backwards \(a_na_{n−1} \dots a_1\).
   We use \(w^R\) for the reversal of string \(w\).
   Then, the reversal of a language \(L\), written \(L^R\), is the language consisting of the reversals of all its strings.
   Think before revealing the answer:
   

   (Wait; then Click)

   If L is a regular languages, then so is \(L^R\).

Practice Proof:

• Claim: Regular languages are closed under union
  In other words: For any regular languages \(L_1\) and \(L_2\), then \(L_1\cup L_2\) is regular
  
  Proof:
  Think before revealing the answer:
  (Hint: Look at the Regular Expression Deffinitions)
  

  (Wait; then Click)

  Since
  \(L_1\) and \(L_2\) are regular, they have regular expressions, say:
  Let \(L_1 = L(R_1) \) and \(L_2 = L(R_2) \).
  Then \(L_1\cup L_2 = L(R_1 + R_2) \) by the definition of the + operator

---

Something to think about: REs...how powerful are they?

For the the Machine Abstraction of Regular Expressions, we can ask:

what problems can they solve?

In other words: Which Language sets can they generate/accept?

Regular Languages are more powerful than Finite Languages (can encompass more)

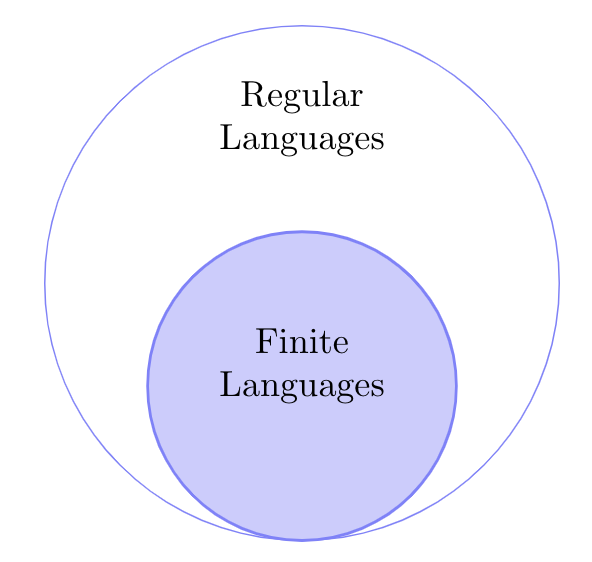
Still confused about RExs? Go to Office Hours with Winnie!! (and with me)

---

Next Class: Finite Automata

---

Homework

[Due for everyone]
[Optional]