Lecture Notes 06:
Practice with Regular Expressions

Outline

This class we'll discuss:

• RE power
• Algorithms: Code, RegExes, and Diagrams
• Intro to Finite Automatons

---

Recap: RegExes, how powerful are they?

For the the Machine Abstraction of Regular Expressions, we can ask:

what problems can they solve?

In other words: Which Language sets can they generate/accept?

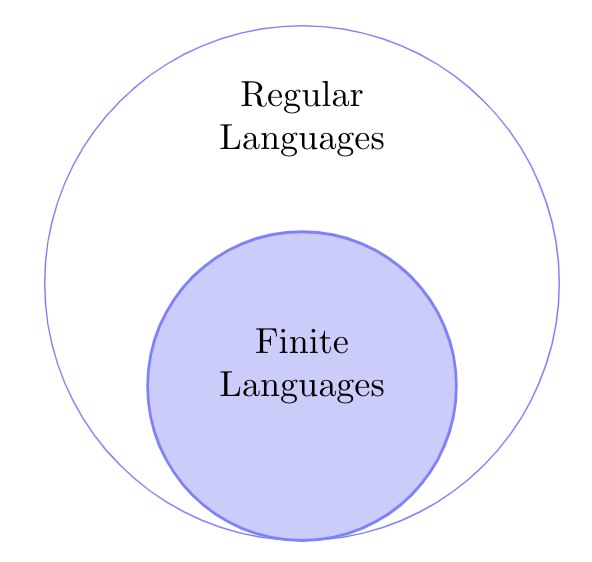
Regular Languages are more powerful than Finite Languages (can encompass more)

Still confused about RExs? Go to Office Hours with Winnie!! (and with me)

---

Algorithms: Code, RegExes, and Diagrams

As we saw above, an algorithm can be encoded as:

1. RegEx
2. (pseudo) Code

But we know that a piece of code can also be drawn using things like a "Flow Diagram"!

In this section, we'll use a special type of diagram called a State Diagram.

State Diagram

A State diagram looks like this:

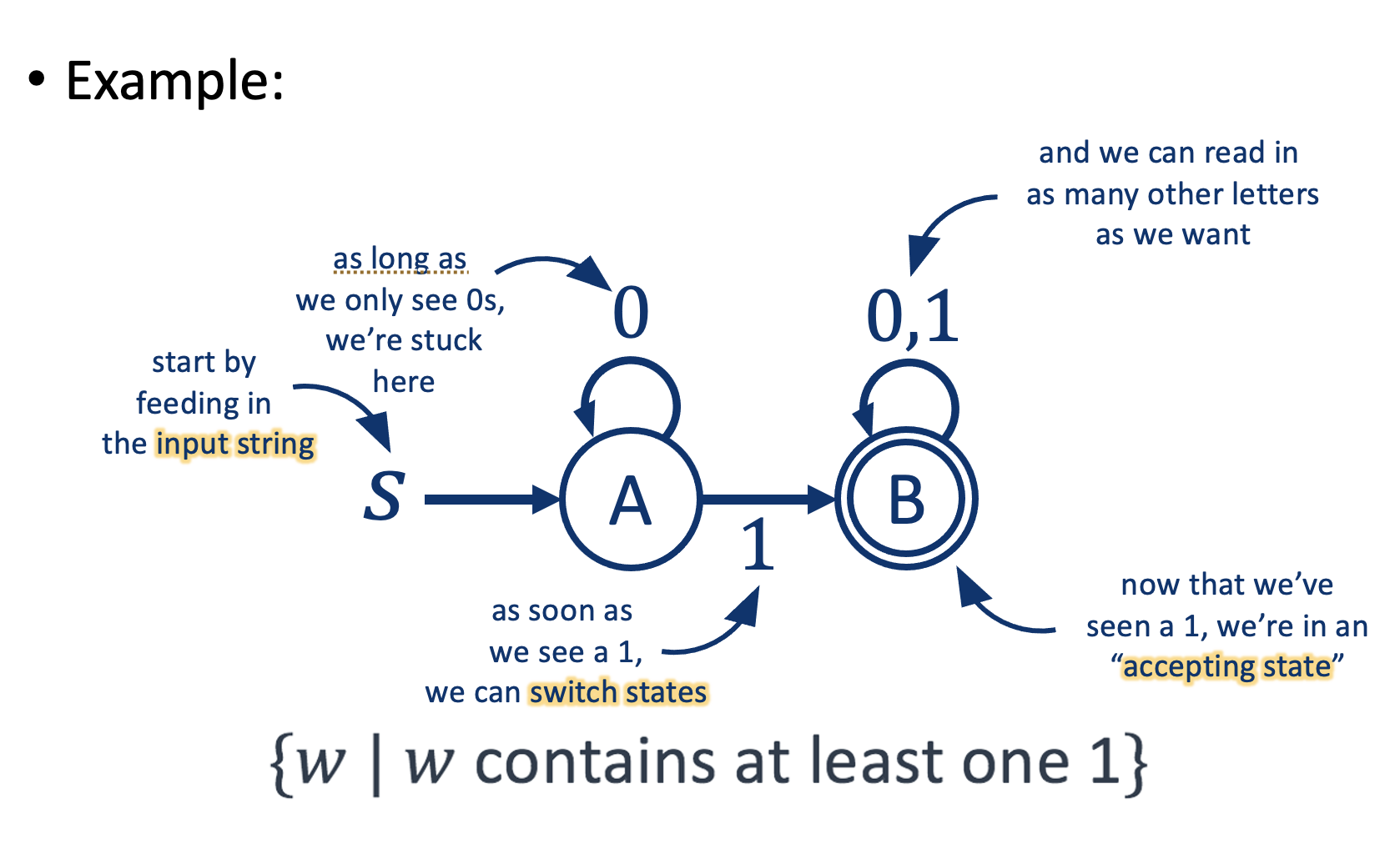
Finite Automaton AKA: Finite State Machine (FSM)

1. Finite number of states
2. Follows Rules that have been programmed beforehand

Operation Examples

Example 01: Processing a String

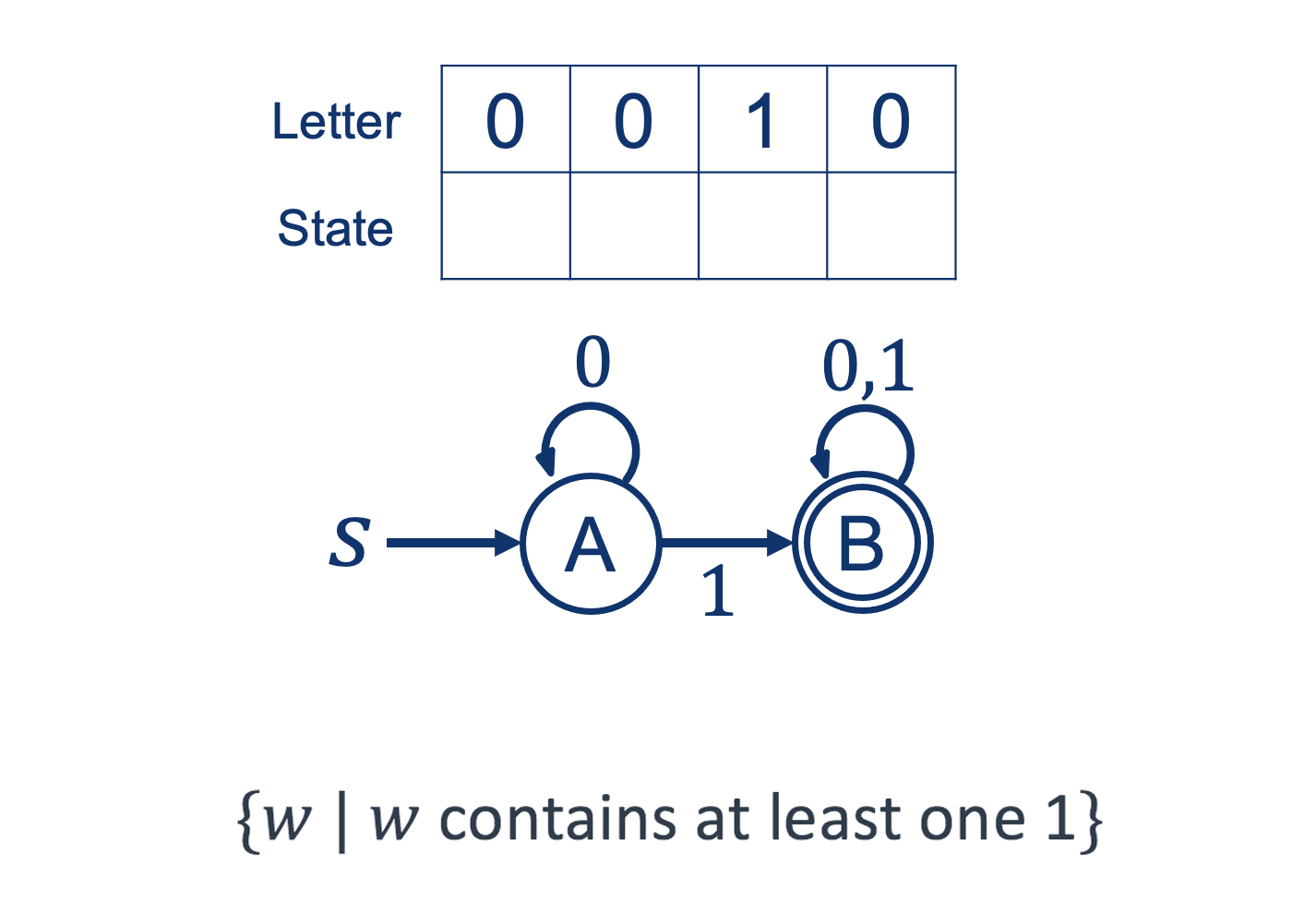
Example 02: Processing a String

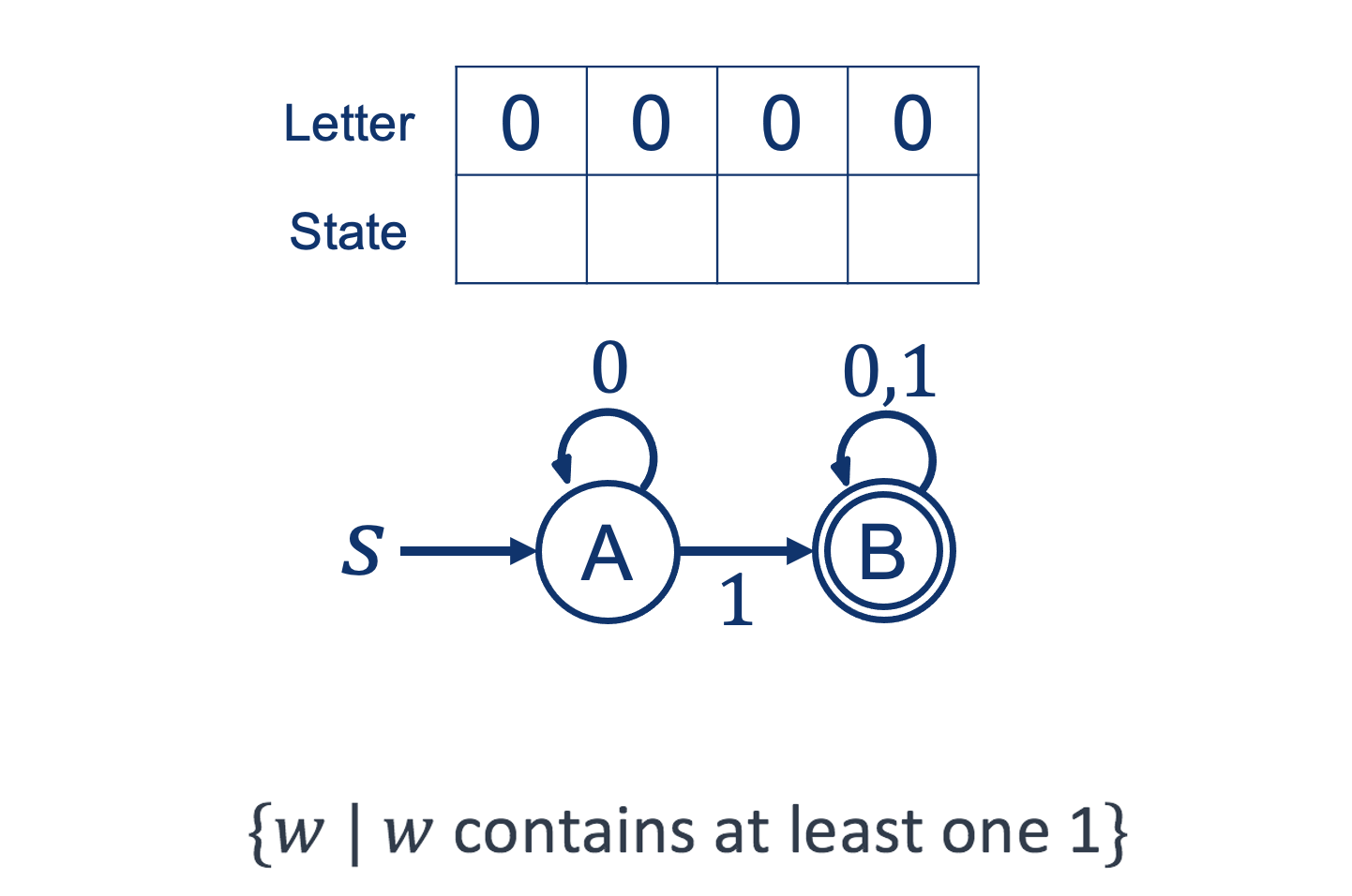
Example 03: Processing a String

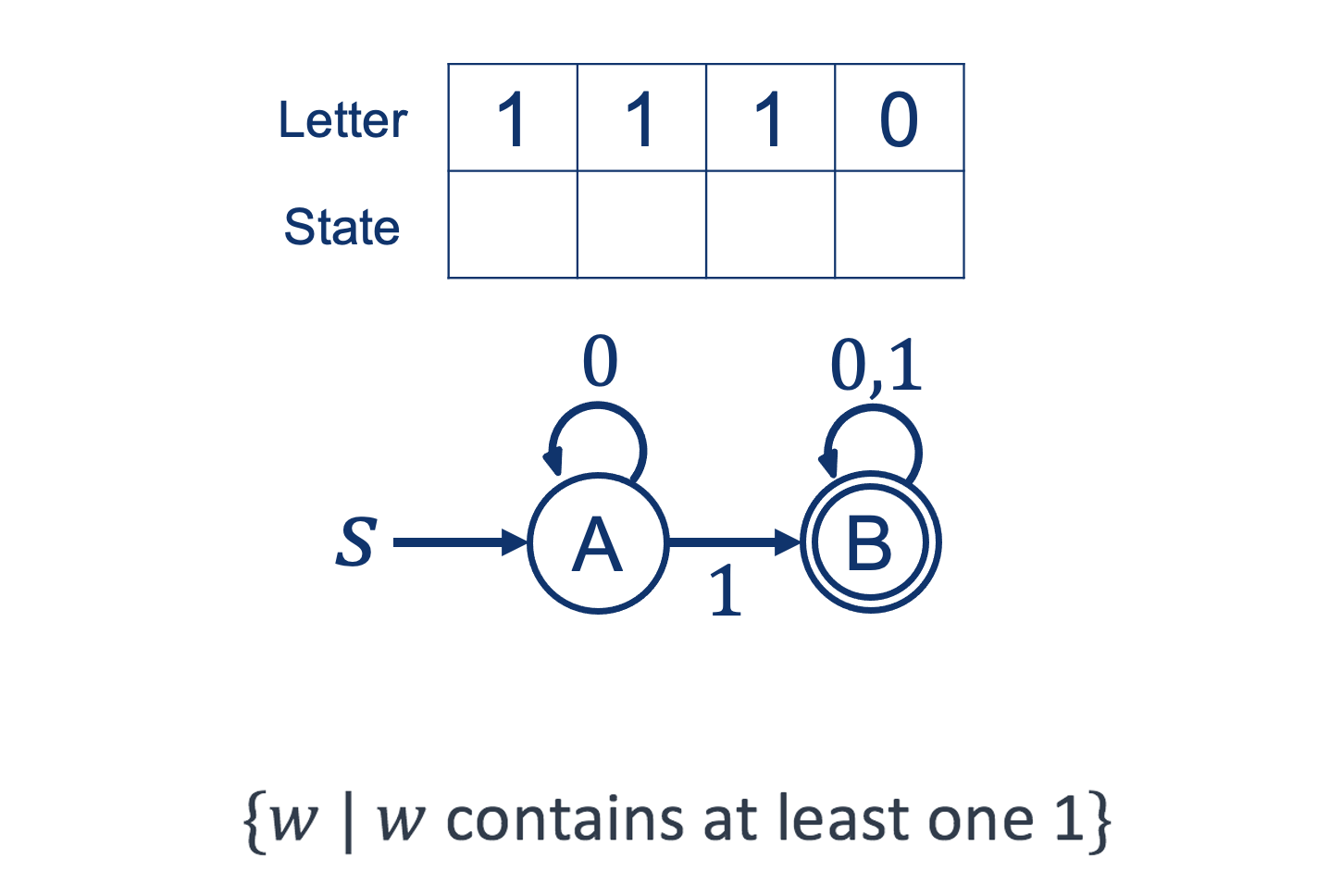Activity 1 [2 minutes]:

---

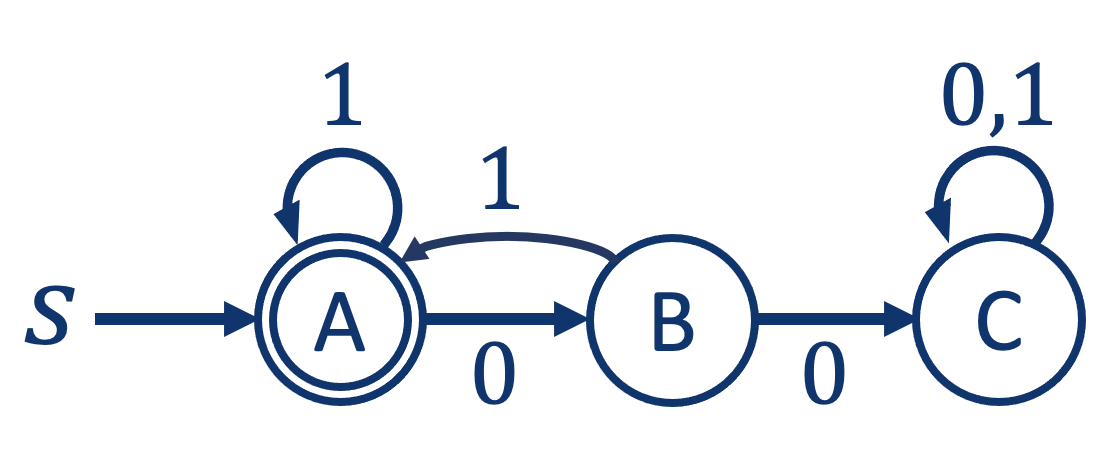
Alphabets and languages

---

Formal Definition

Our Last Example:

Operators in FSMs: OR

How might we handle a language that contains an or?

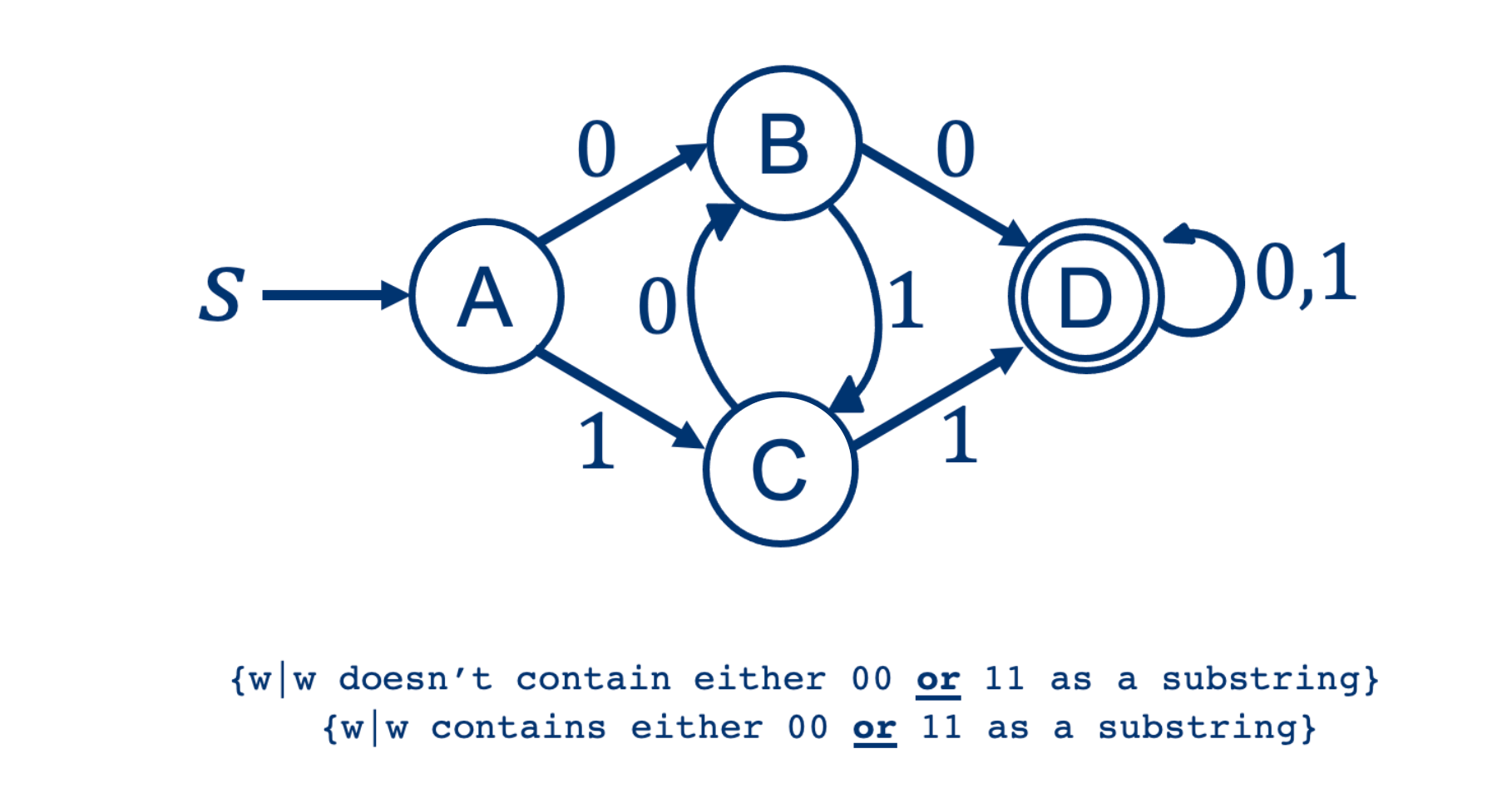
Example: {w|w doesn’t contain either 00 or 11 as a substring}



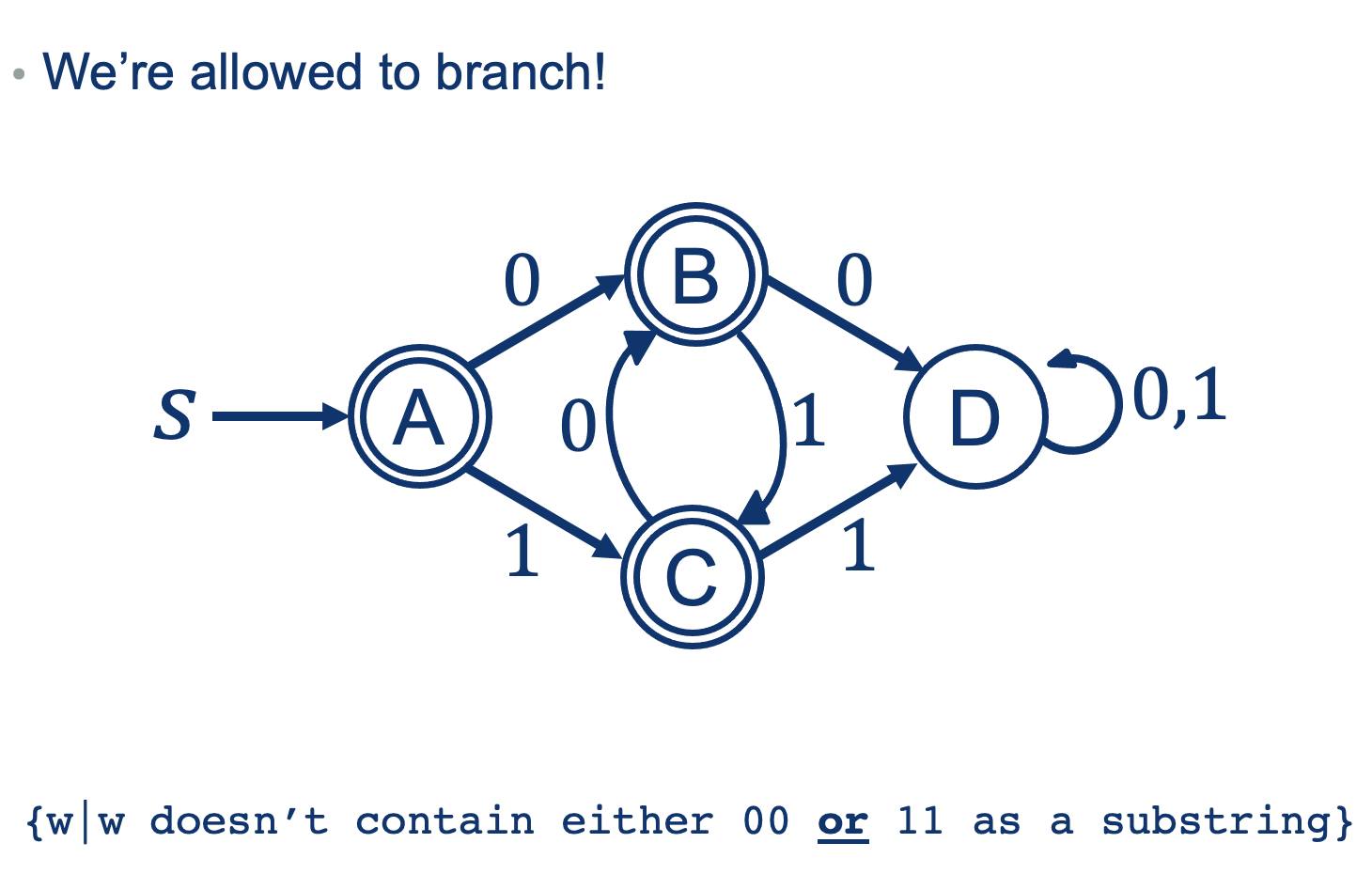
Let's try one basic example:



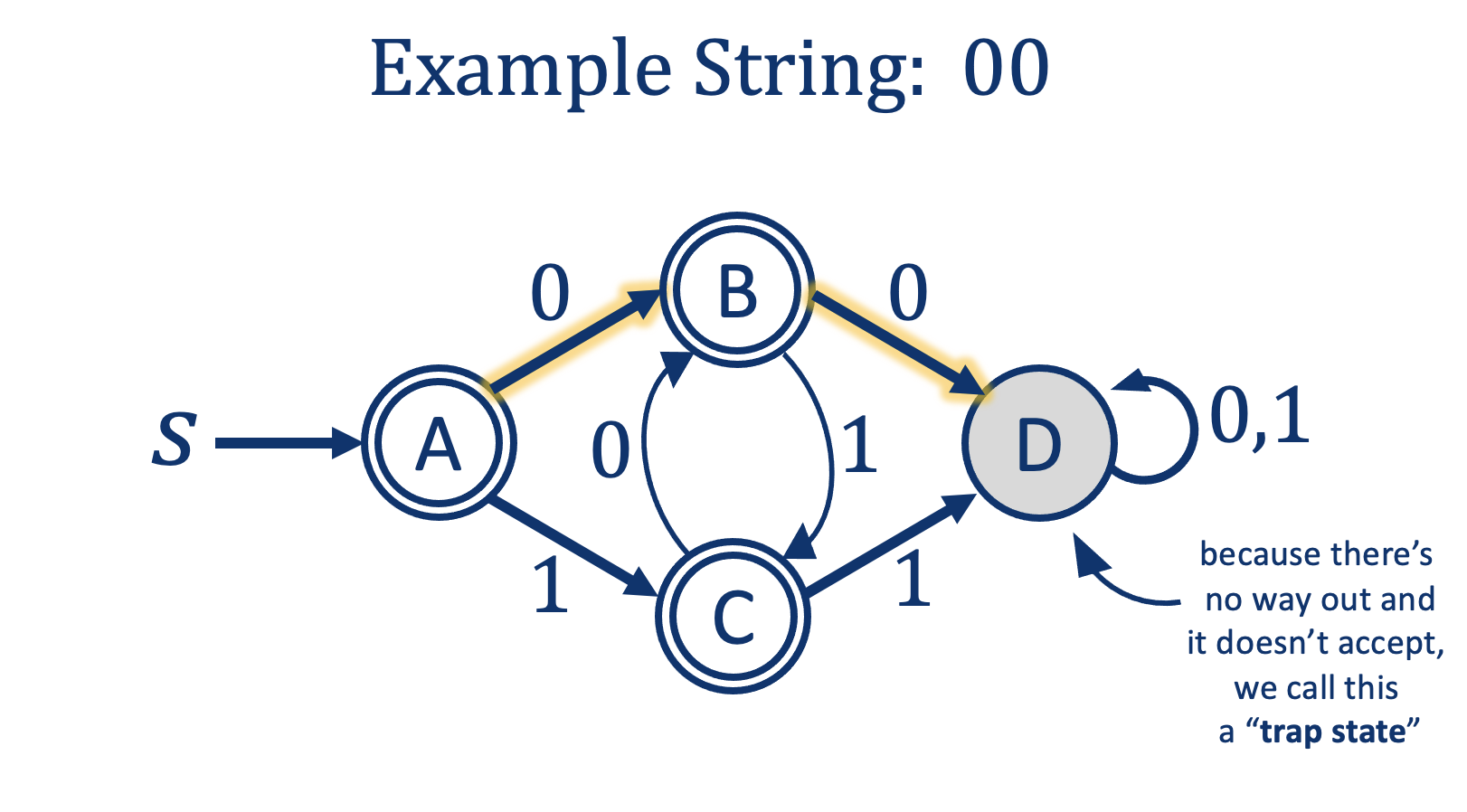Activity 2 [2 minutes]:


Activity 3 [2 minutes]:

---

Useful Properties

These are some properties that can help you deduce, generalize, or analyze FSMs with respect to their RegEx and Regular Languages.

Complement

IF a Language \(L_1\) is recognizable by an FA \( M_1\),
is language \( (L_1)^{c} \) also recognizable by some FA?

Or in other words, \[\exists M_2 \quad | \quad L(M_2) = L(M_1)^{c} \]

Intersection

Activity 4 [2 minutes]:
Example:

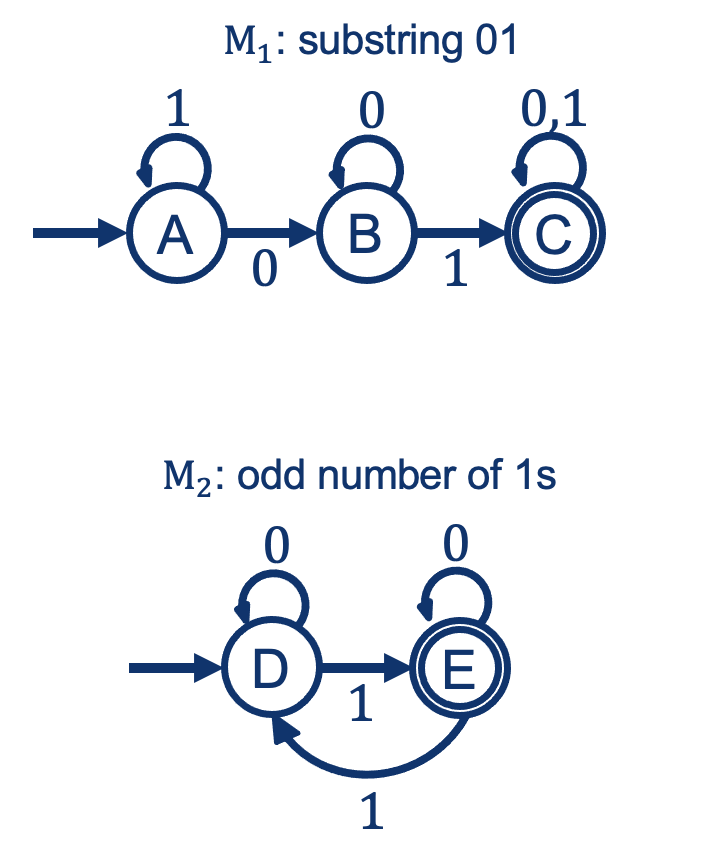
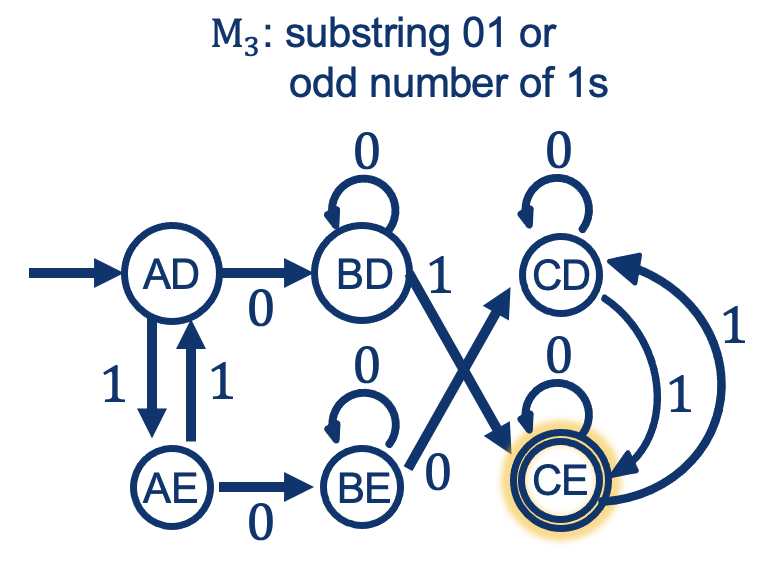
Intersection: General Rule

Union

Activity 5 [2 minutes]:
Example:

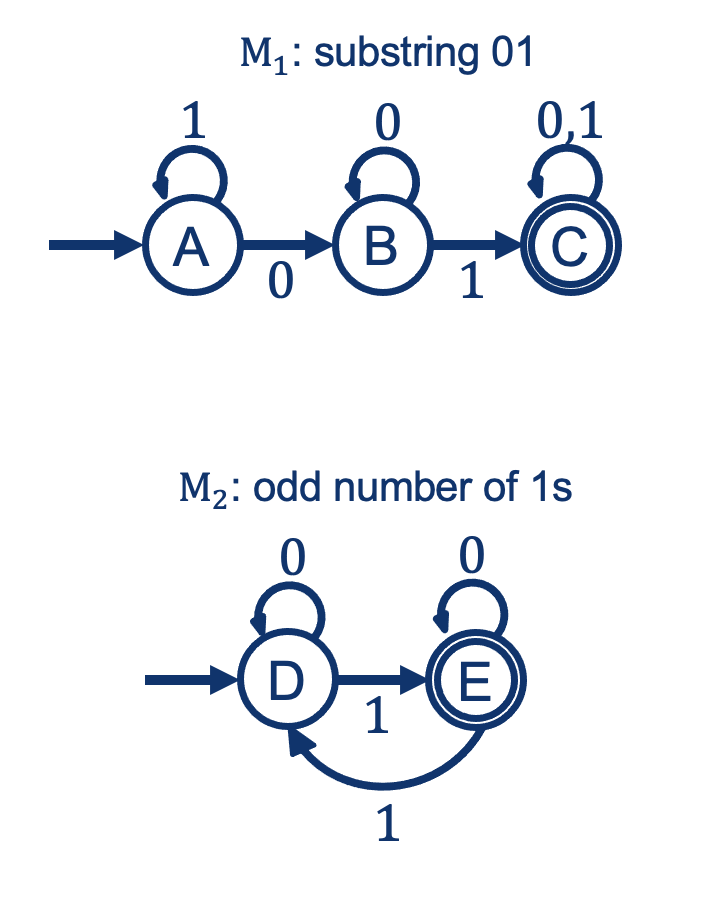
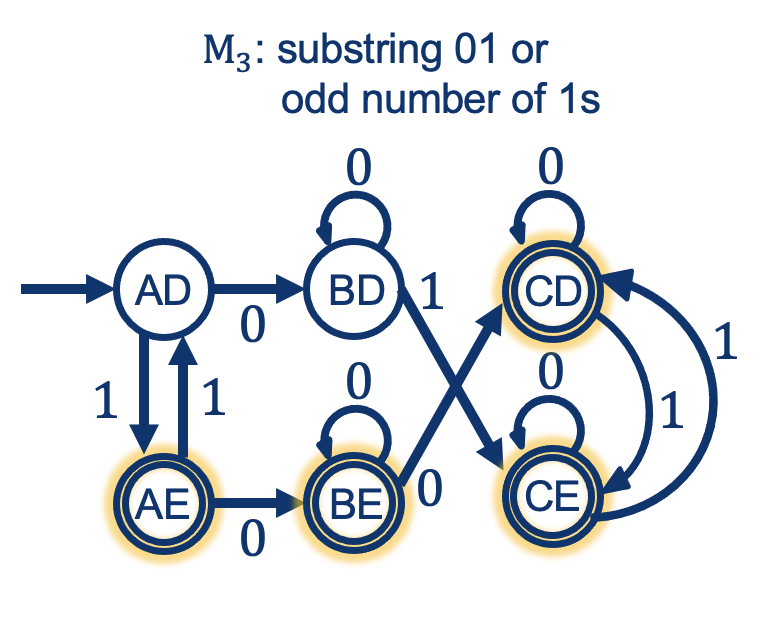
Union: General Rule