Lecture Notes 04:
Regular Languages and Regular Expressions

Outline

This class we'll discuss:

• What are we doing?
• Regular Expressions
• Regular Languages

---

A Map of what we'll be doing in class

What are we going to do?

As we mentioned last class, We are going to analyze what types of problems can be solved with minimal "machinery".

• what can we do with a specific type of "machine", or in other words: "what types of problems can we solve?"
• Another way to look at it is: "Giva problem A, what is the minimal "machine" that can help me solve it.

We are going to work up from basic machines up to the modern computer.

How are we going to do? it

Since we are not really going to build those machines in hardware, we will need to "represent" them symbolically.

We will be building symbolic machines to solve problems of greater and greater complexity.

A candidate "simple" problem:

\[ \begin{align*} & 1001011 \\ & + \\ & 0111011 \end{align*} \]

While this might look simple, this is really a very advanced problem, it requires that the machine know:

• what 1001011 is
• what + means
• what 0111011 is, and
• How to do it

In other words, performing Arithmetic operations is a few "machines" away.

Step 1: recognizing a pattern

You can think of a machine that recognizes things and can clasify them as being in a set of known elements or being outside that set of know elements.

With our symbolic replicas, a first task would be to be able to specify the structure or pattern of a set of symbols that we would like to be able to recognize.

How to build a "recognizing" machine

Activity 1 [1 minute]:
Can you think of a super simple (mechanical) machine that "recognizes" things?

Activity 2 [1 minute]:
Can you think of a super simple (mechanical) machine that "recognizes" a pattern (sequence of things)?

Regular Expressions are like lock mechanisms that can be built to recognize one or many "keys".

---

Regular Expressions

An expression is a combination of objects and operators that can be "resolved" into a value.

In Arithmetic, the objects are numbers, and the operators are: \( + \text{, } - \text{, } * \text{, } ÷ \text{, }\) etc.
A (correct) arithmetic expression looks like this: \[ (27 - 6)* 2\]

A Reglar Expression (RE or RegEx) is an algebraic way to describe a set of words.

In reglar expressions, we also have objects and symbols, which can be combined to form an expression that might look like this: \[ 0^*(101 + 11011)0^* \]

Another way you'll see this written is as: \( \mathrm{L} (R) \), (for some RE \(R\))
which refers to the Language (set of words) described by the expression ( \(R\) ) inside parenthesis.

We sometimes refer to the Language with some symbol like \(\mathrm{L}_A\), where language \(L\) has some property \(A\).

Defining a Regular Expression

We will follow a sequence of steps to understand how to build regular expressions.
First, we'll need some basic definitions

RE Definitions

• A set is a group of items under the same property.
  We'll use set operations like union (\(\cup\)), concatenation, and complement ( of \(A\) is \( \bar{A} \));
• \( \emptyset \) : the set with no members is called the empty set: \( \emptyset \) or \(\{ \} \) ;
• \(\Sigma\): an alphabet \(\Sigma\) is a nonempty set of symbols (letters), for example:
  • \(\Sigma = \{a \text{, } b \text{, } c \text{, } \dots\}\), or
  • \(\Sigma = \{0,1\}\)
• \(w\): a string (or word) \(w\) is a sequence of symbols from an alphabet.
• \(\epsilon\): a string with no letters is the empty string \(\epsilon\);
• a Language is a set of words.

The following are some examples:

• The set with no elements: \( \emptyset \) or \(\{ \} \)
• The set with the the empty string as its single element : \(\{ \epsilon \} \)
• the set with three words: \(\{ Larry \quad , \quad Curly \quad , \quad Moe \} \)
• The Language with all two-bit binary words: \(\{ 00 \quad , \quad 01 \quad , \quad 10 \quad , \quad 11\} \)
• In the last example, the alphabet \(\Sigma = \{0,1\}\)

Regular Operations

• The Union of two sets \(A\) and \(B\): \(A\cup B\) is the set that has both the members of \(A\) and from \(B\)
  For example: If \(A: \{ white \text{, } blue\}\), and \(B: \{ duck \text{, } rabbit\}\),
  The union would be: \(A\cup B: \{ white \text{, } blue \text{, } duck \text{, } rabbit\}\)
  
  Another example: If \(A: \{ 0 \text{, } 1\}\), and \(B: \{ x \text{, } y\}\),
  The union would be: \(A\cup B: \{ 0 \text{, } 1 \text{, } x \text{, } y\}\)


• The Concatenation of two sets \(A\) and \(B\): \(A\circ B\) or simply \(AB\) is a set.
  This is the set that has a sequences of two symbols: a member of \(A\) before a member of \(B\): \(AB: \{ whiteduck \text{, } whiterabbit \text{, } blueduck \text{, } bluerabbit \}\).
  
  
  Note that in the expression \(AB\), we're saying "any element from \(A\) followed by any element from \(B\)", not "all of \(A\) followed by all of \(B\)"!
  
  Another example: If \(A: \{ 0 \text{, } 1\}\), and \(B: \{ x \text{, } y\}\),
  \(AB: \{ 0x \text{, } 0y \text{, } 1x \text{, } 1y \}\).


• The Star (or Kleene Star) operator \(A^*\) is a unary operator that returns the set of sequences that have zero or more symbols from a set \(A\):
  \(A^*: \{ \epsilon \text{, } white \text{, } blue \text{, } whiteblue \text{, } bluewhite \text{, } whitewhiteblue \text{, } whitebluewhite \text{, } \dots\}\)
  
  Another example: If \(A: \{ 0 \text{, } 1\}\),
  \(A^*: \{ \epsilon \text{, } 0 \text{, } 1 \text{, } 01 \text{, } 10 \text{, } 001 \text{, } 010 \text{, } \dots\}\)
  
  You can think of it as a zero or more concatenation operator.

Definition of Regular Expressions (Recursively)

Basic (axiomatic) definitions:

• Basis 1: \(\emptyset\) is a regular expression, and \( \mathrm{L} (\emptyset) = \emptyset\)
• Basis 2: \(\epsilon\) is a regular expression, and \( \mathrm{L} (\epsilon) = \{\epsilon\} \)
• Basis 3: \(a\) is a symbol, then \(a\) is a regular expression, and \( \mathrm{L} (a) = \{a\} \)

Recursive extensions:

• Alternation:
  One expression or another,
  If \(\mathrm{R}_1\) and \(\mathrm{R}_2\) are regular expressions,
  then \(\mathrm{R}_1 + \mathrm{R}_2\) is a regular expression,
  and \( \mathrm{L} (\mathrm{R}_1 + \mathrm{R}_2) = \mathrm{L} (\mathrm{R}_1) \cup \mathrm{L} (\mathrm{R}_2)\)
  
  Example:
  If \( R_1 = 0\) and \( R_2 = 1\),
  what is \( R_3 = R_1 + R_2\) ?
  

  Think before revealing the answer:

  (Wait; then Click)

  \(R_3 = 0 + 1\)

  
  what is \( \mathrm{L} (\mathrm{R}_1 + \mathrm{R}_2) \)?

  Think before revealing the answer:

  (Wait; then Click)

  \( \mathrm{L} (\mathrm{R}_3 ) = \{ 0, 1\} \)



• Concatenation:
  If \(\mathrm{R}_1\) and \(\mathrm{R}_2\) are regular expressions,
  then \(\mathrm{R}_1 \mathrm{R}_2\) is a regular expression,
  and \( \mathrm{L} (\mathrm{R}_1 \mathrm{R}_2) = \mathrm{L} (\mathrm{R}_1) \mathrm{L} (\mathrm{R}_2)\)
  
  Example:
  If \( R_3 = (0 + 1)\) and \( R_4 = 1\),
  what is \( R_5 = R_3 R_4\) ?
  

  Think before revealing the answer:

  (Wait; then Click)

  \(R_5 = (0 + 1)1\)

  
  what is \( \mathrm{L} (\mathrm{R}_3 \mathrm{R}_4) \)?

  Think before revealing the answer:

  (Wait; then Click)

  \( \mathrm{L} (\mathrm{R}_5 ) = \mathrm{L} ( \; (0 + 1)1 \; ) = \{ 01, 11\} \)



• Kleene star:
  If \(\mathrm{R}_1\) is a regular expression,
  then \(\mathrm{R}^*_1\) is a regular expression,
  and \( \mathrm{L} (\mathrm{R}_1^*) = \big( \mathrm{L} (\mathrm{R}_1) \big)^* \)
  
  Example:
  If \( R_5 = (0 + 1)1 \),
  what is \( R_5^*\) ?
  

  Think before revealing the answer:

  (Wait; then Click)

  \(R_5^* = ( \; (0 + 1)1 \; )^*\)

  
  what is \( \mathrm{L} (\mathrm{R}_5^*) \)?

  Think before revealing the answer:

  (Wait; then Click)

  \( \mathrm{L} (\mathrm{R}_5^* ) = \mathrm{L} ( \; ((0 + 1)1)^* \; ) = (\mathrm{L} ( \; (0 + 1)1 \;))^* = ( \; \{ 01, 11\} \; )^* \)
  \( = \{ \epsilon, \quad 01, \quad 11, \quad 0101, \quad 0111, \quad 1101, \quad 1111, \quad 010101, \quad \dots \} \)

Precedence rules are: do parenthesis first, then do star first, then concatenation, then union.

Let's trt some exercises:

Activity 4 [2 minutes]:
What is the expression that gives us all binary strings?
Describe it in words or with any notation you find useful. We'll develop the rigorous notation later.
Hints:
1) what is the alphabet \(\Sigma\)?
2)Which operator might help us expand this into the correct language \(\mathrm{L}_b\)?

Activity 5 [2 minutes]:
What is the expression that gives us all binary strings that begin with a 1?

Activity 6 [2 minutes]:
What is the expression that gives us all binary strings that begin with a 1, end with a 0, and have an even number of digits?

The RegEx Minigolf!

Activity 7 [5-10 minutes!!]:
Make teams of 2 or 3 and complete the following challenges.
Let me know when your team is done.

---

Regular Languages

A regular language is one that can be generated using a regular expression.

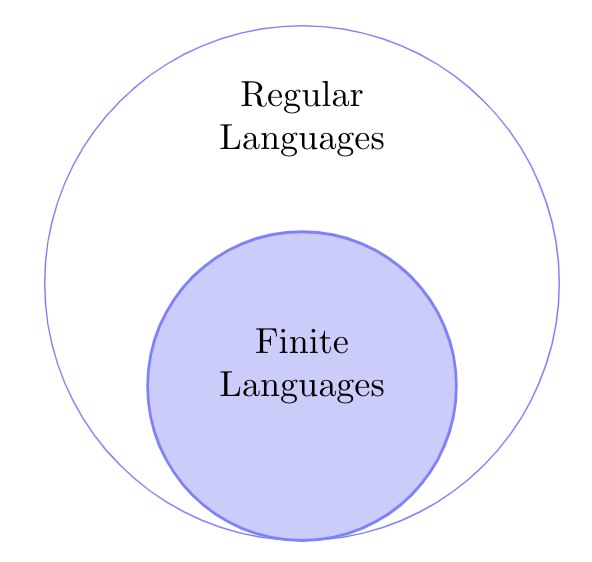
Activity 8 [1 minute]:
Answer the following questions:

• Are all finite languages regular?
• Are all regular languages finite?

(Wait; then Click)

Regular Languages are more powerful!

Properties

The following properties are true about regular languages:

• Claim: Regular languages are closed under union
• Claim: Regular languages are closed under concatenation
• Claim: Regular languages are closed under intersection
• Claim: Regular languages are closed under complement
• Claim: Regular languages are closed under difference
• Claim: Regular languages are closed under reversal

Practice Proof!

Claim: Regular languages are closed under union

Tips: Use the axioms defined above!
In particular:

• A regular language is, by definition, the language generated by a regular expression.
• The Alternation rule

---

Next Class: Overleaf + Latex, Regex Recap, and Intro to Finite Automata!!

---

Homework

[Optional] How would you build a "flowchart" to solve this regex: