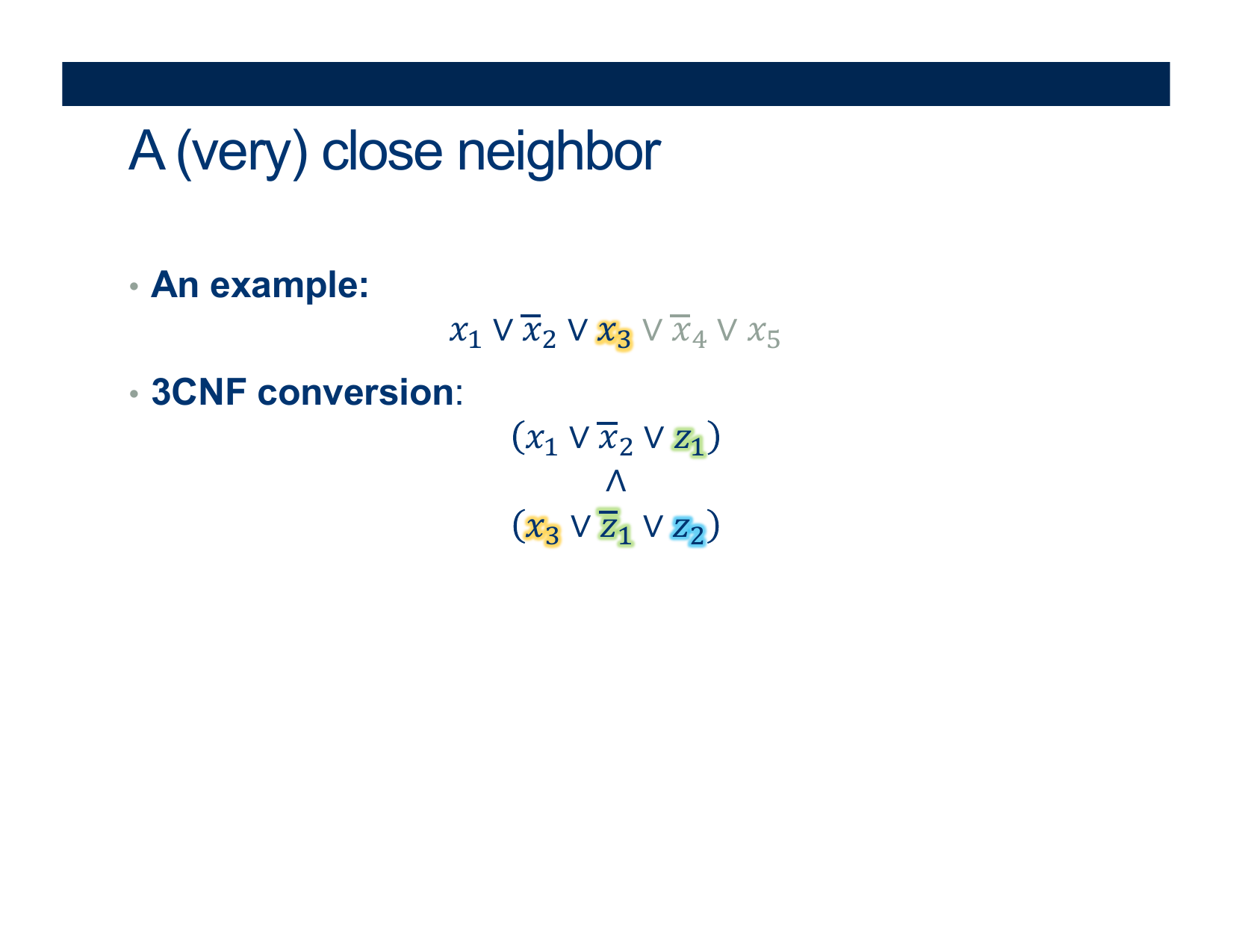Lecture Notes 34: UnRecognizable Ls and Poly-Time Reductions in NP-C
Outline
This class we'll discuss:
- Grading for the last part of the course
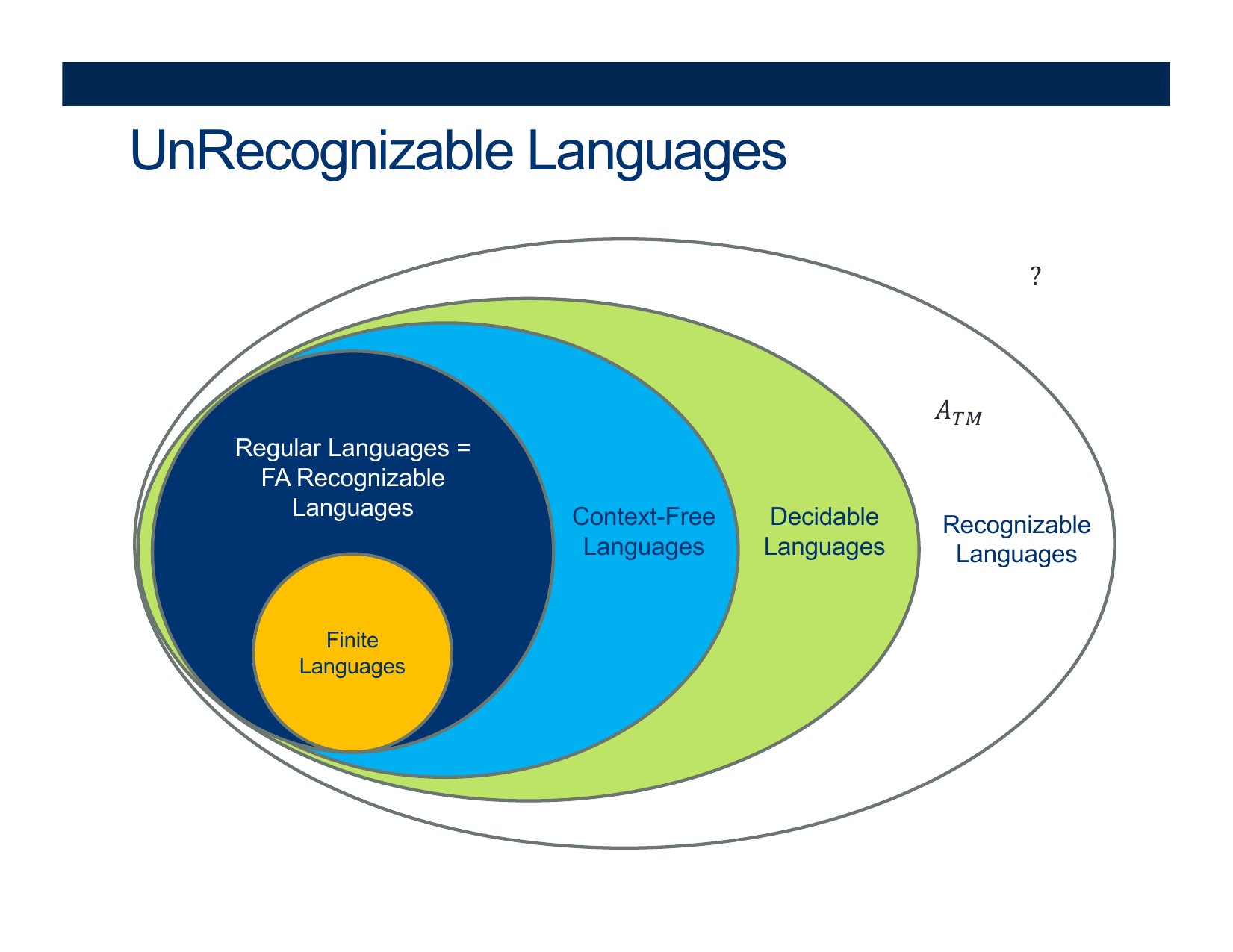
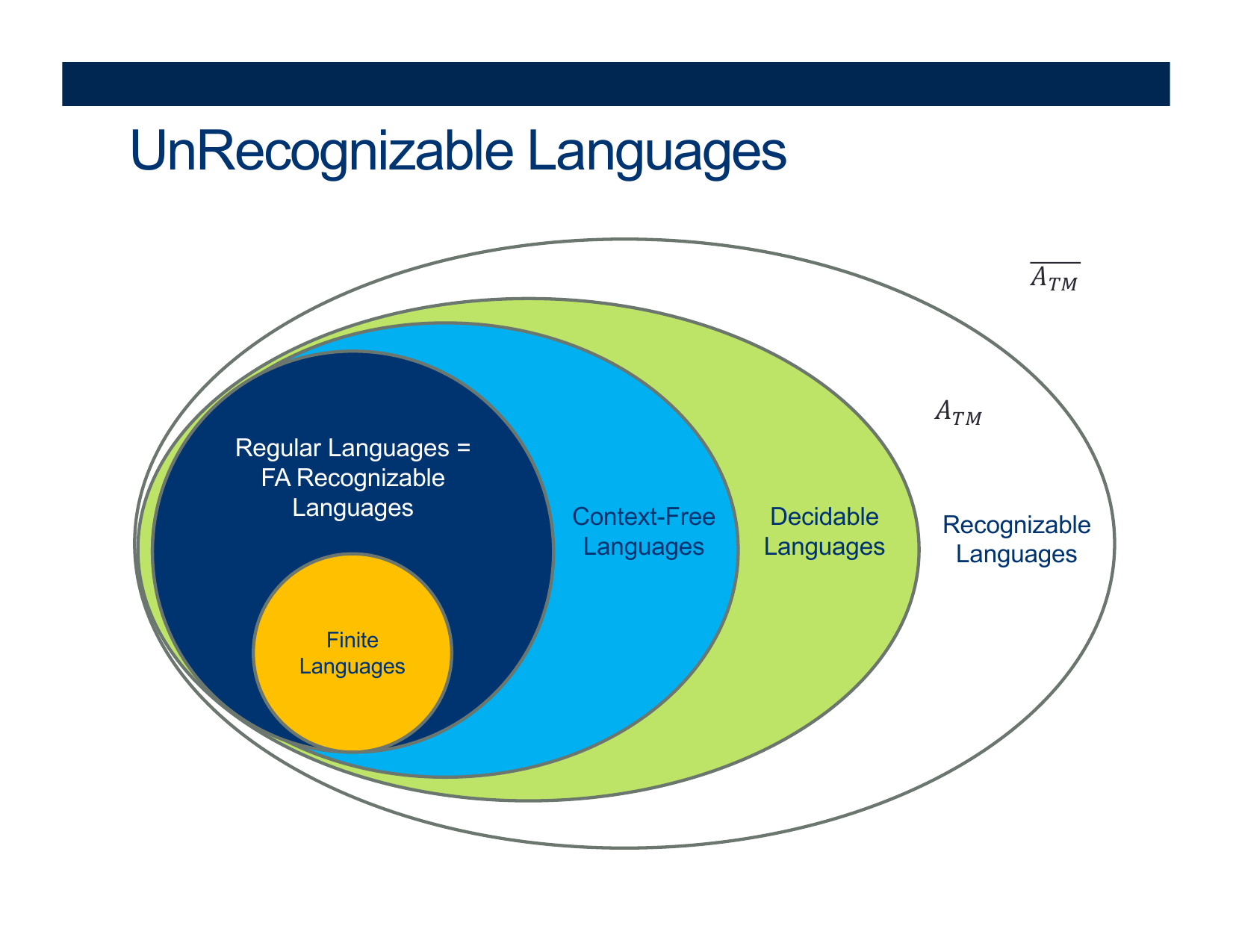
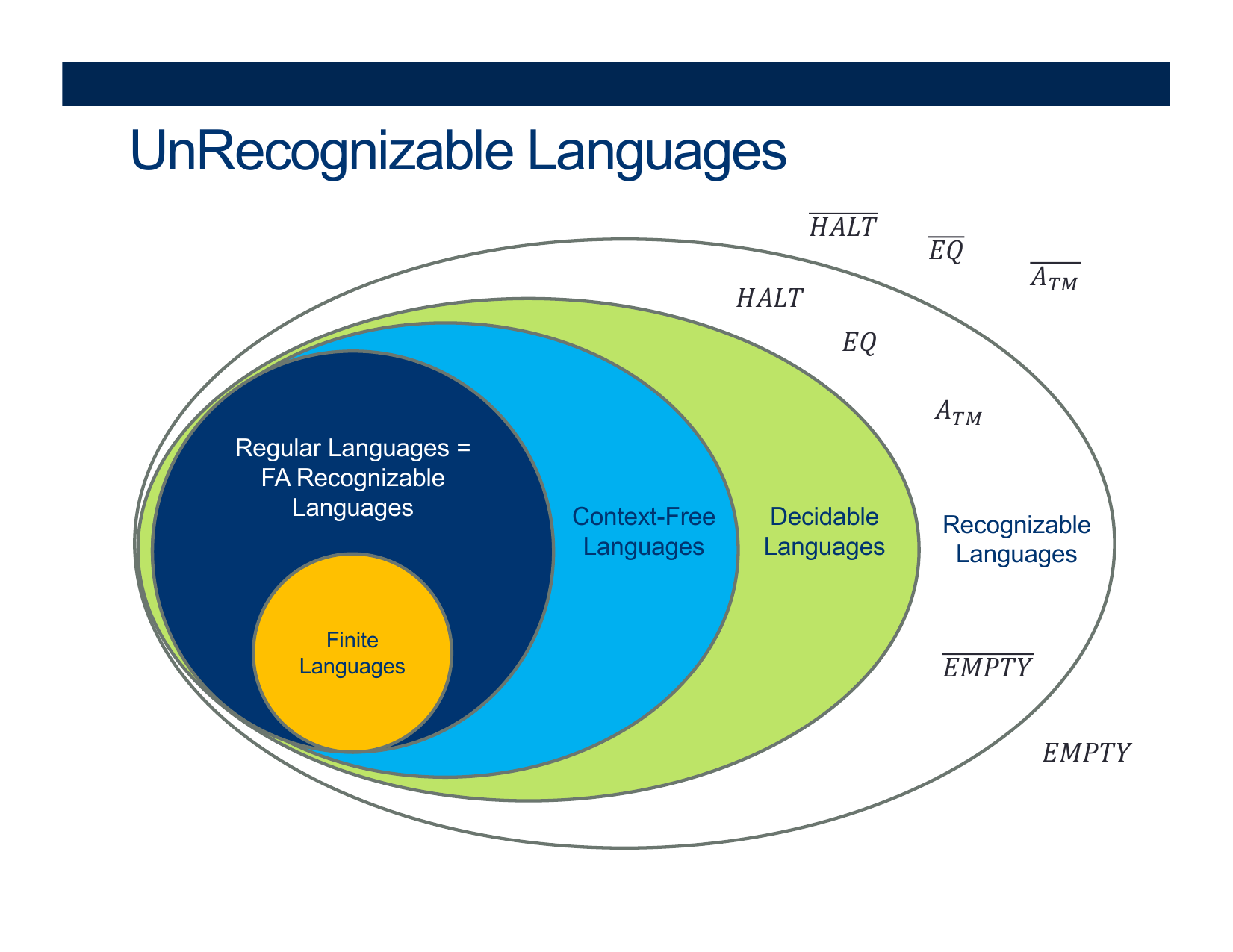
- UnRecognizable Languages
- Poly-time reductions in NP-Complete
- Final Exam format
Grading for the last part of the course
The following are the ways in which we will grade the final part of course:
- We will work on Problem Set 8 during next week of classes... IN-Class. The idea is that you use the class time as a sort of "Discuss and Solve" session, and I get to give you instant feedback.
- I will grade each of you during class when you are done with it
- If you finish it and have nothing else to show me (see next point), you are free to leave!
-
For your recovery points, you have:
- One resubmit assignment (5 questions ...that you got wrong in A1-A6)
- A points-back resubmission of your midterm
The BEST way for me to grde you on these two is IN-CLASS while we work on assignment 8.
If you have already made a video, don't worry, you can also show it to me in-class and I'll give you instant feedback and let you tweak the submissions.
Recap: P vs NP vs NP-Hard vs NP-Complete






Activity [2 minutes] Find, at least 3 more!:
(Wait; then Click)


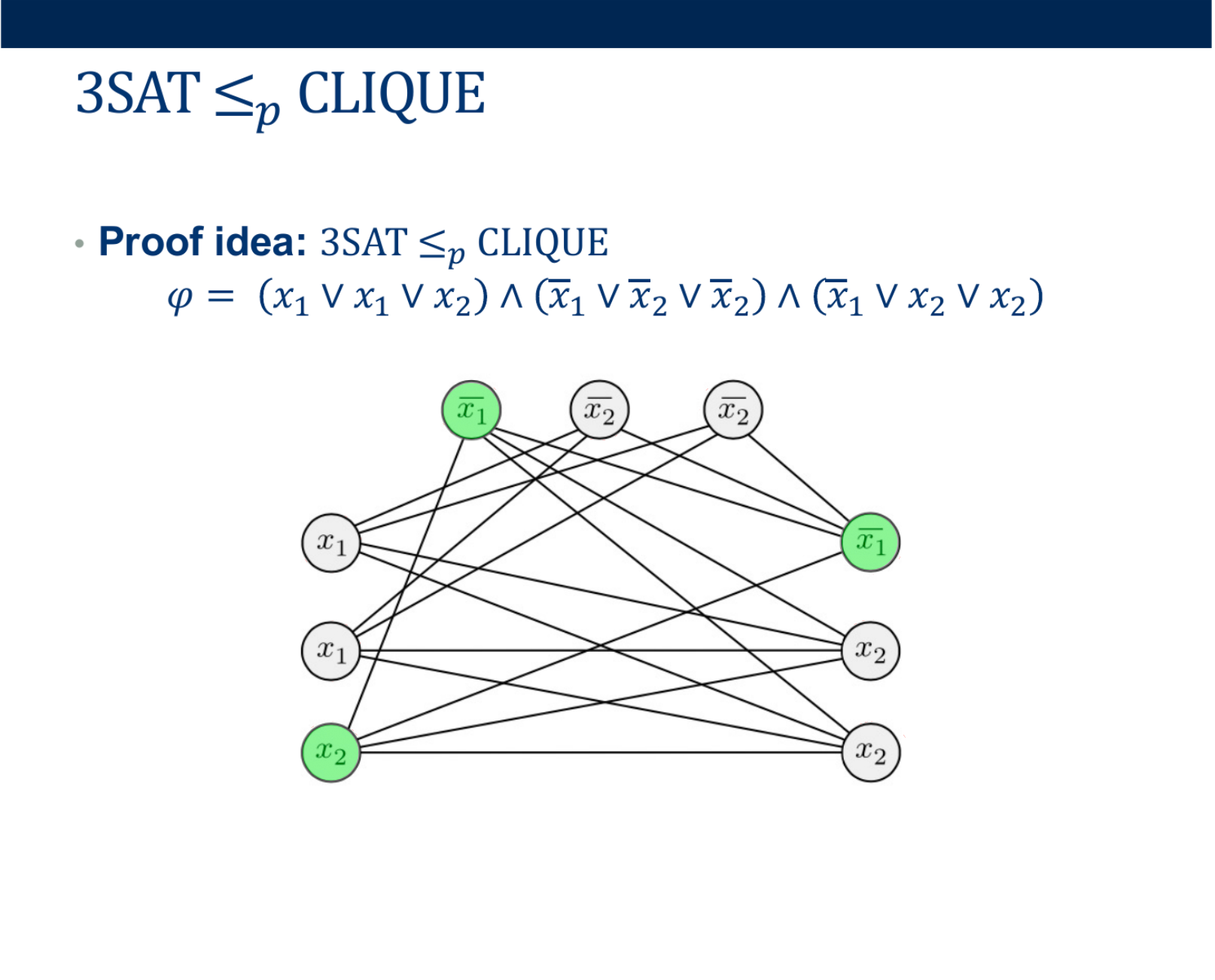
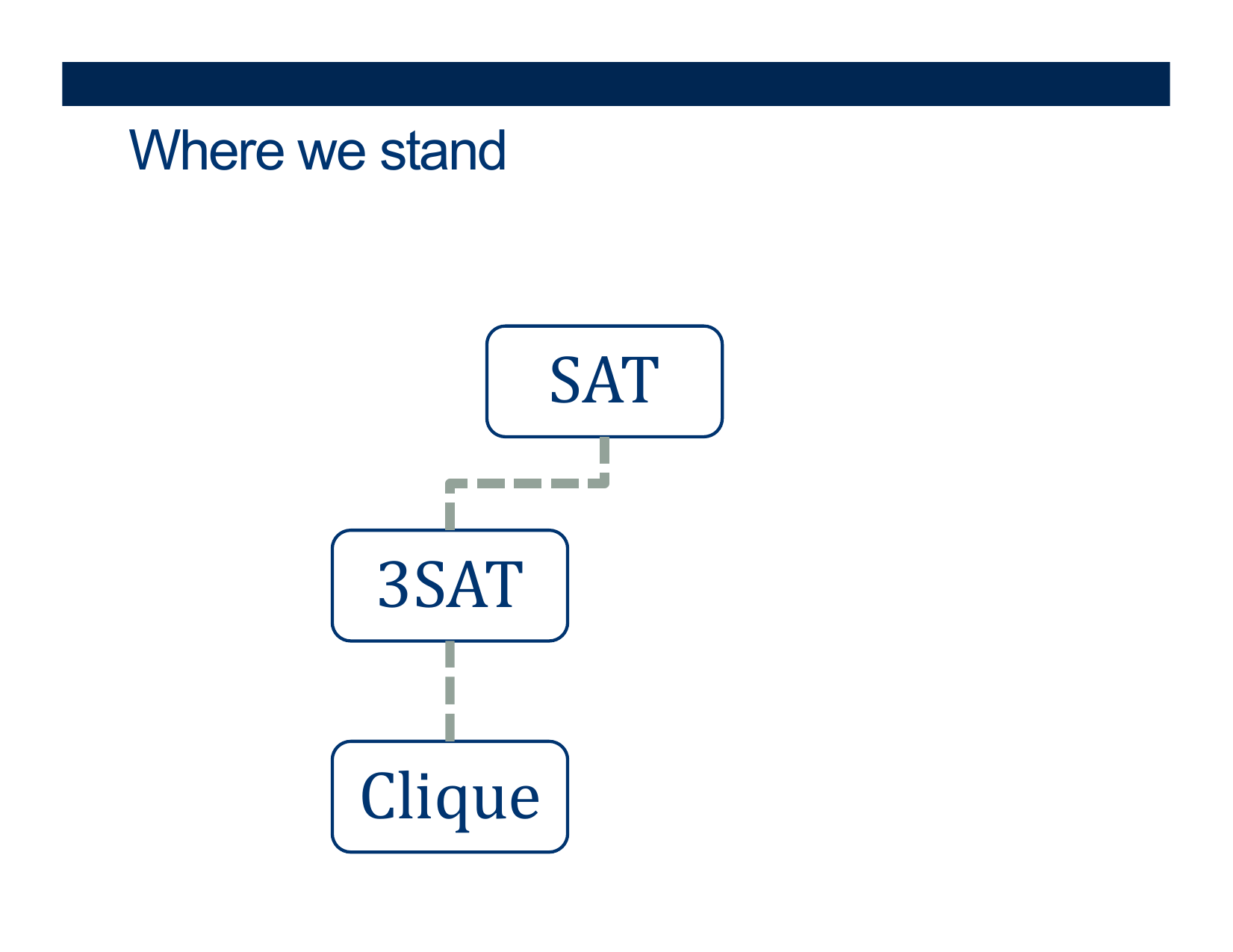
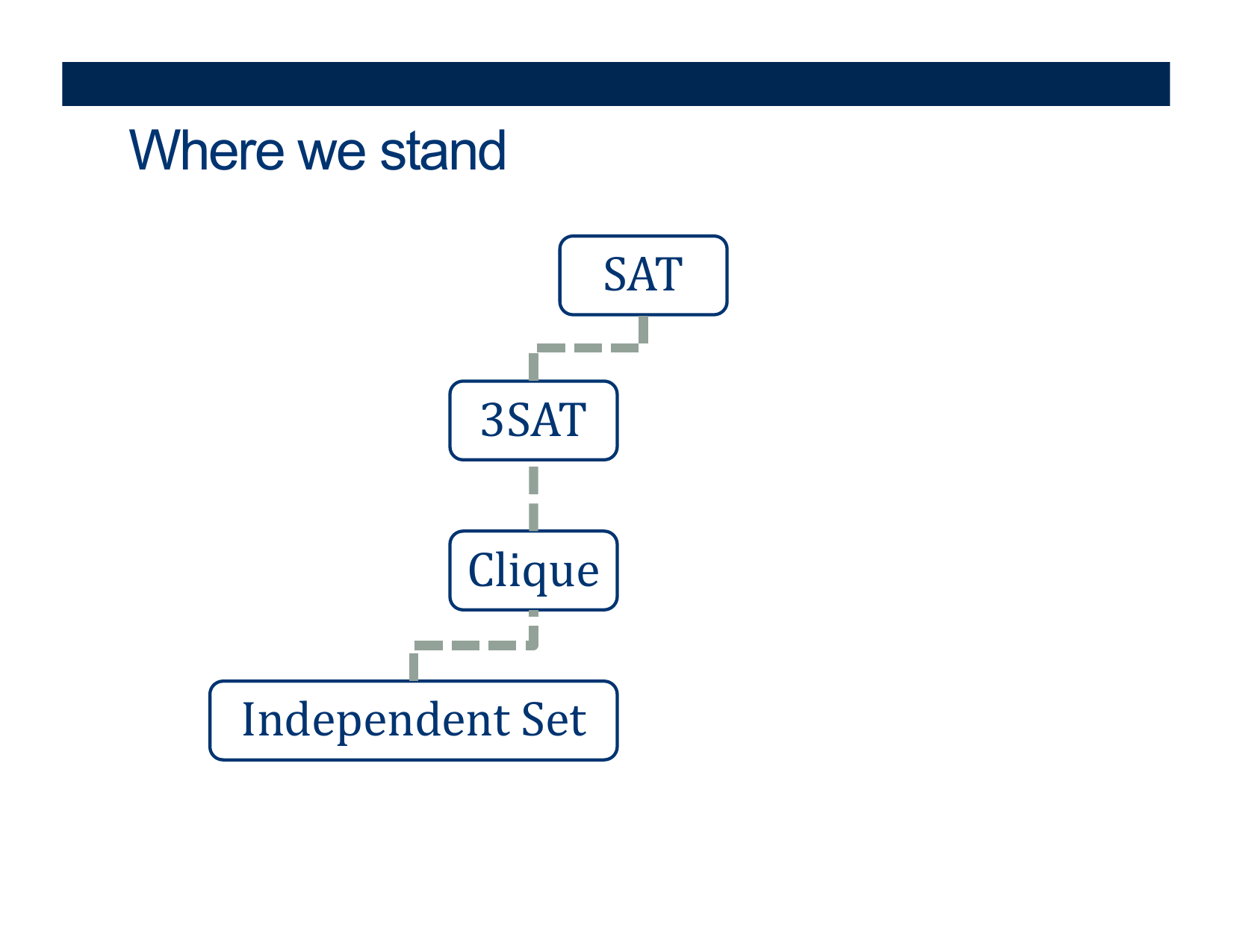
 More Polynomial-Time Reductions in NP-Complete
More Polynomial-Time Reductions in NP-Complete


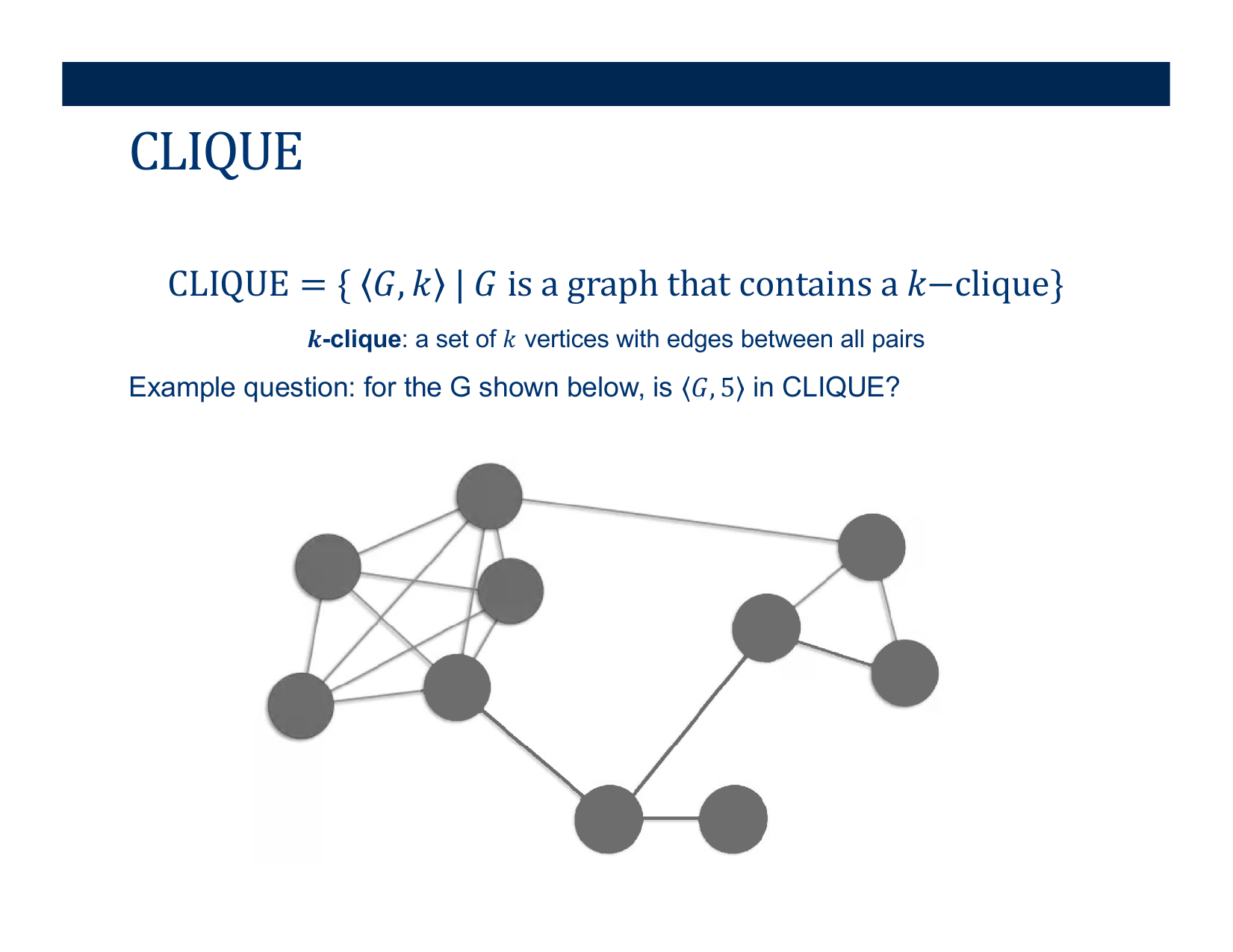
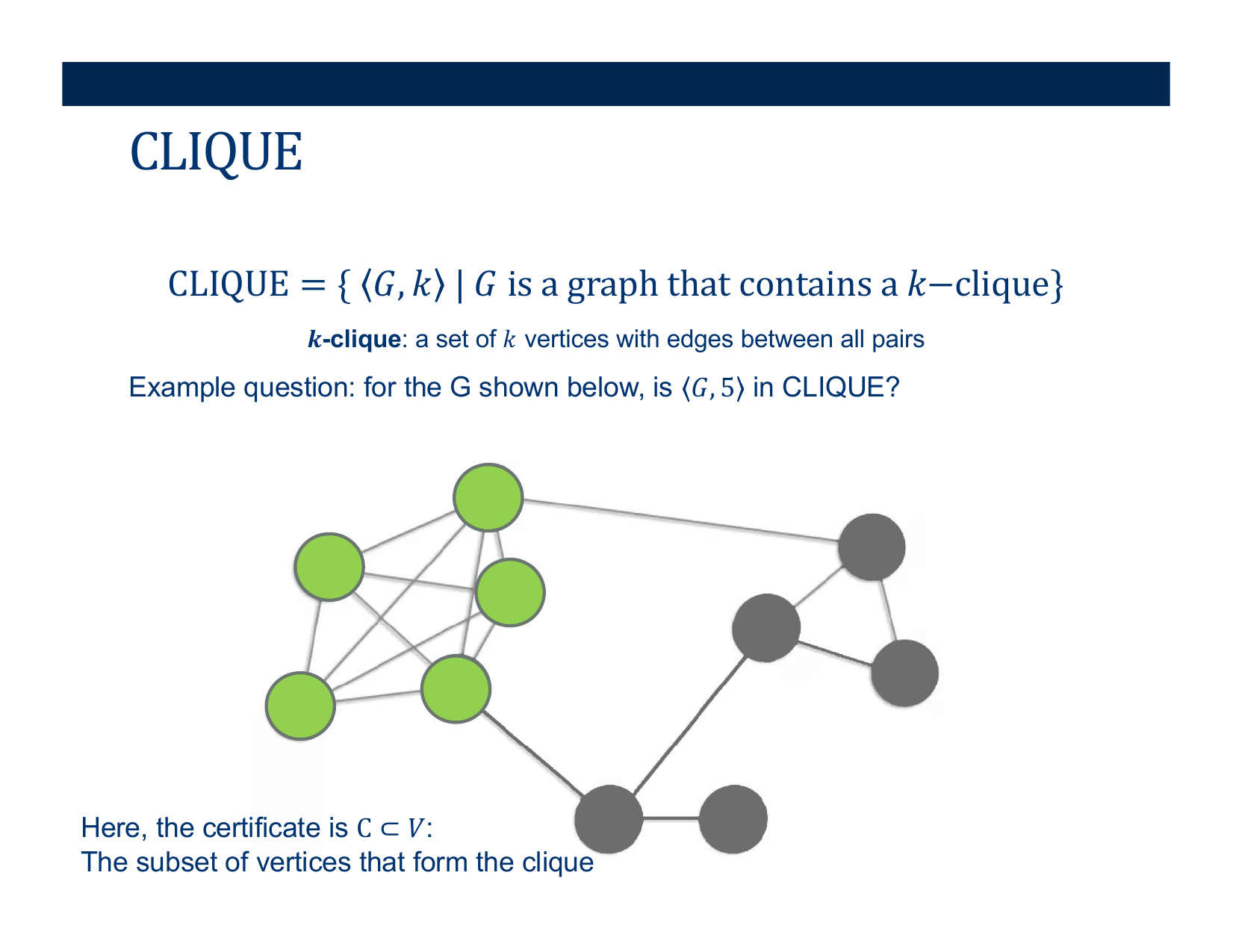

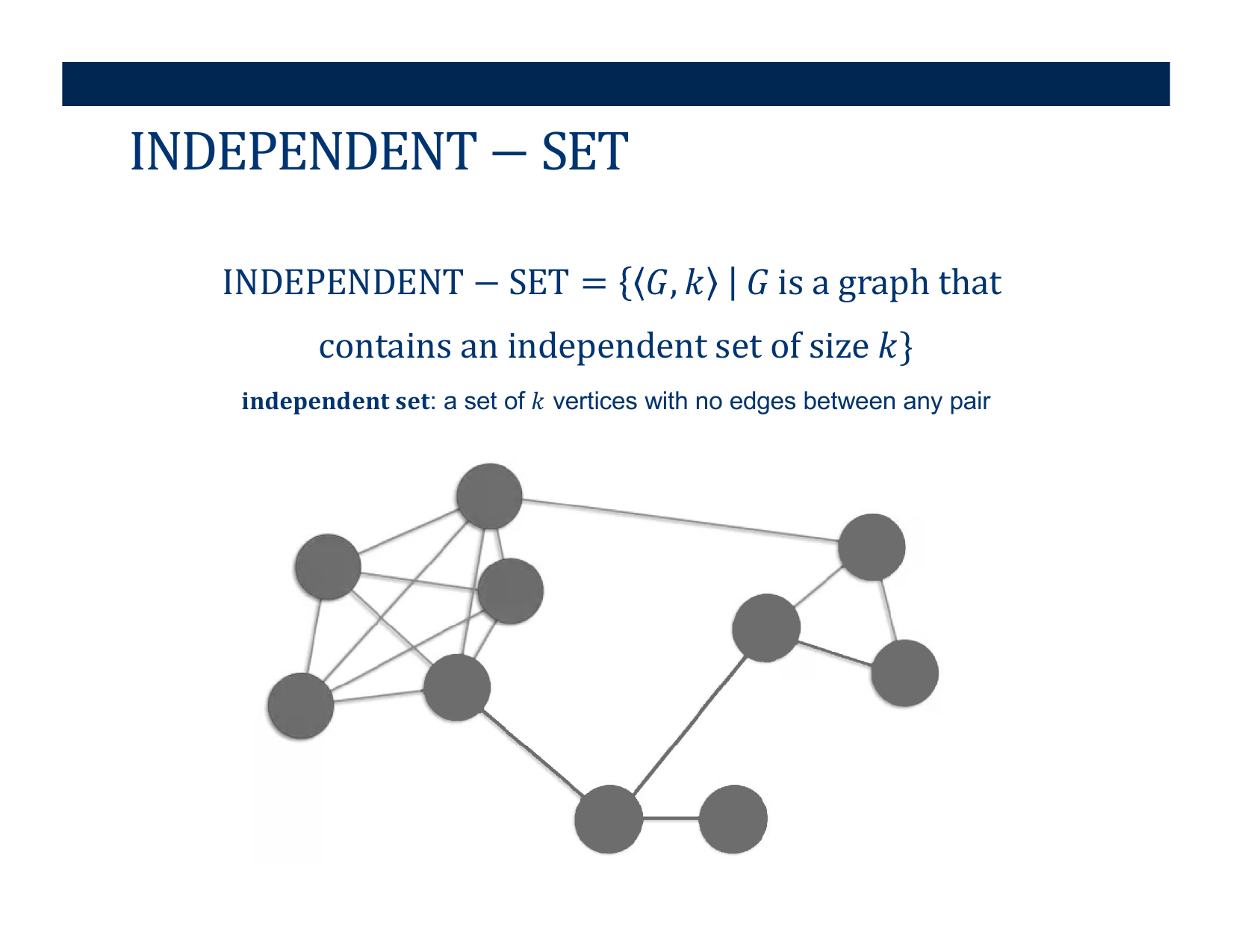
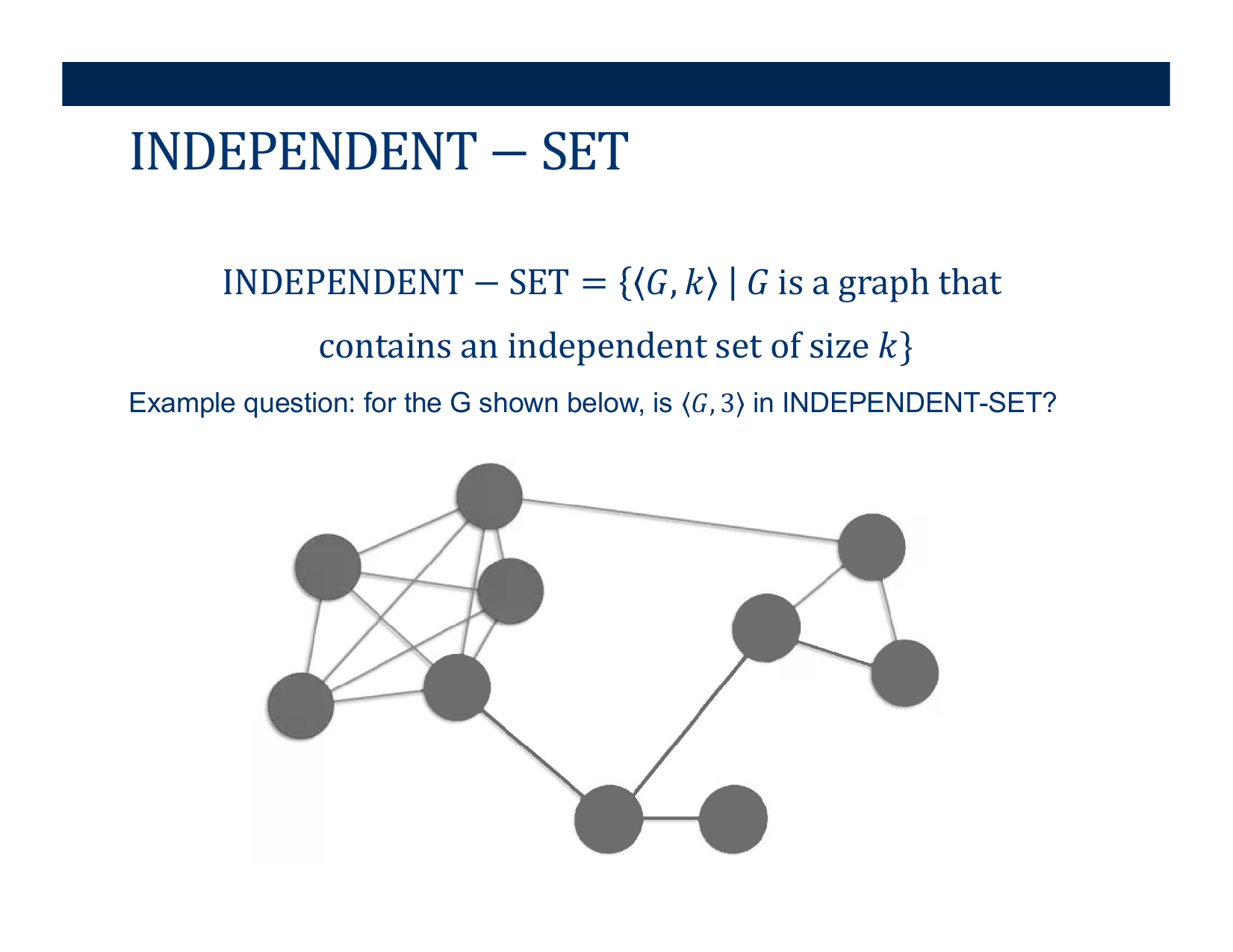









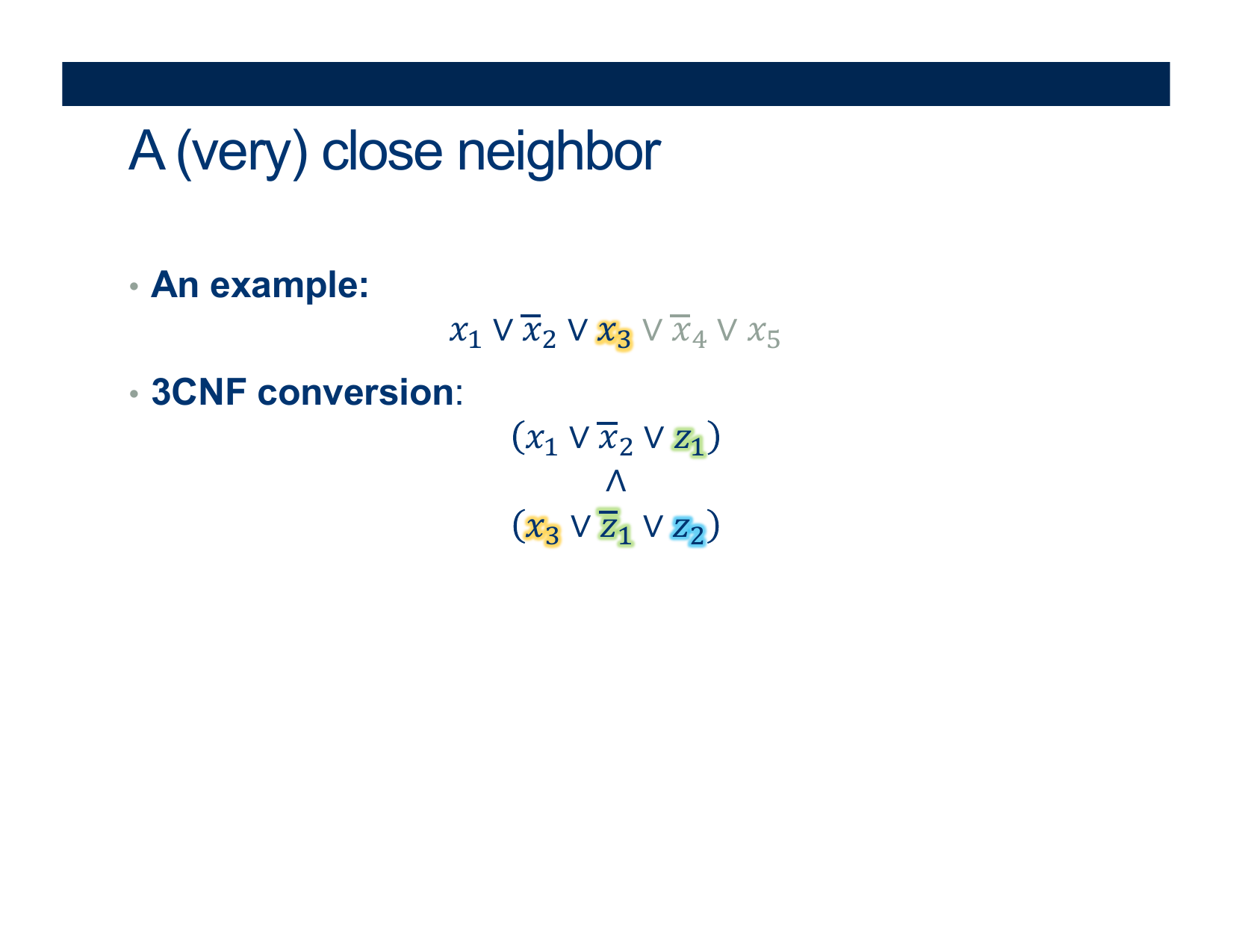

Activity [2 minutes]
Complete the following:
What would a Certificate look like for each of the following Problems?
- Deciding if \( \Phi \) belongs in SAT
- Deciding if \( \Phi \) belongs in 3SAT
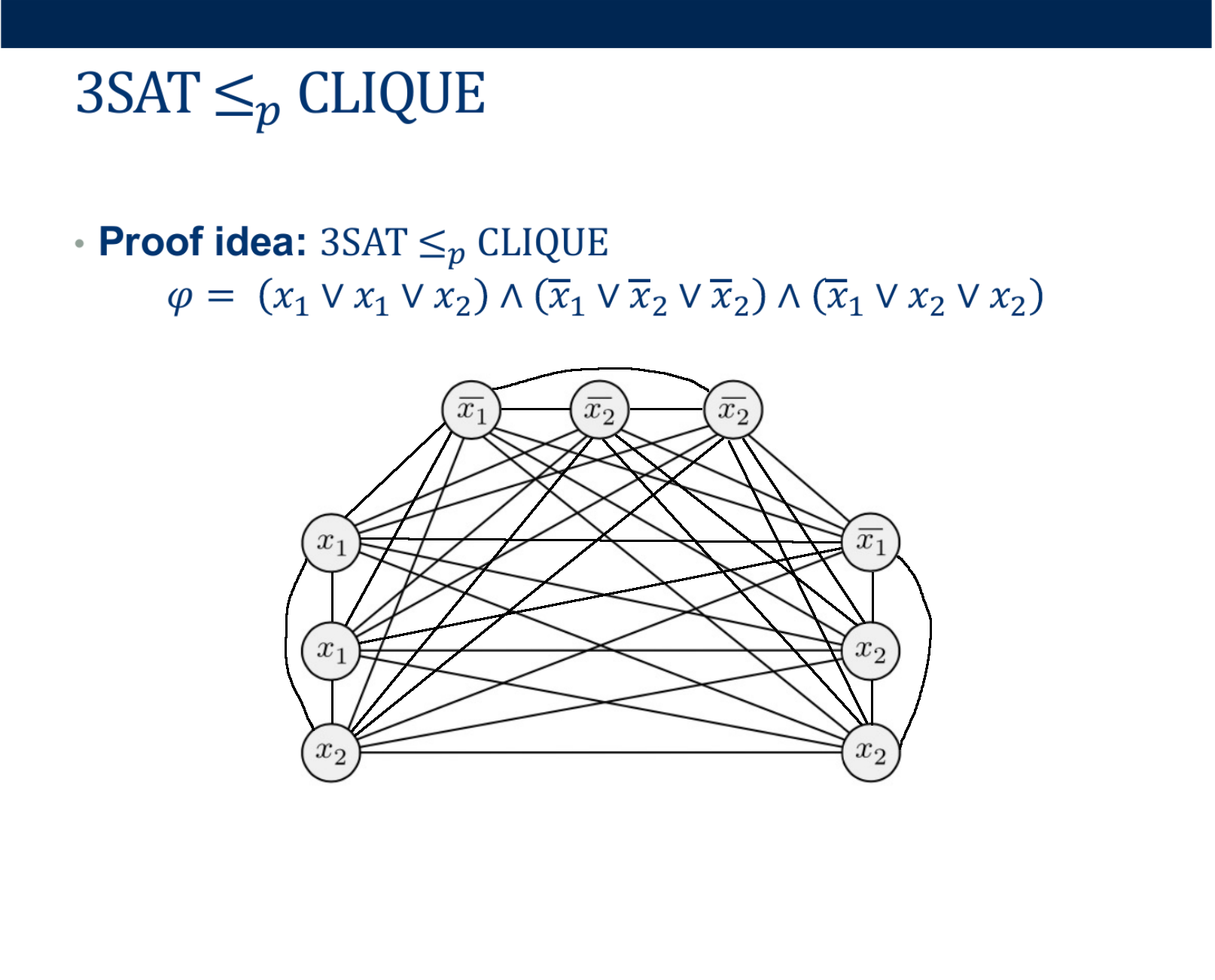
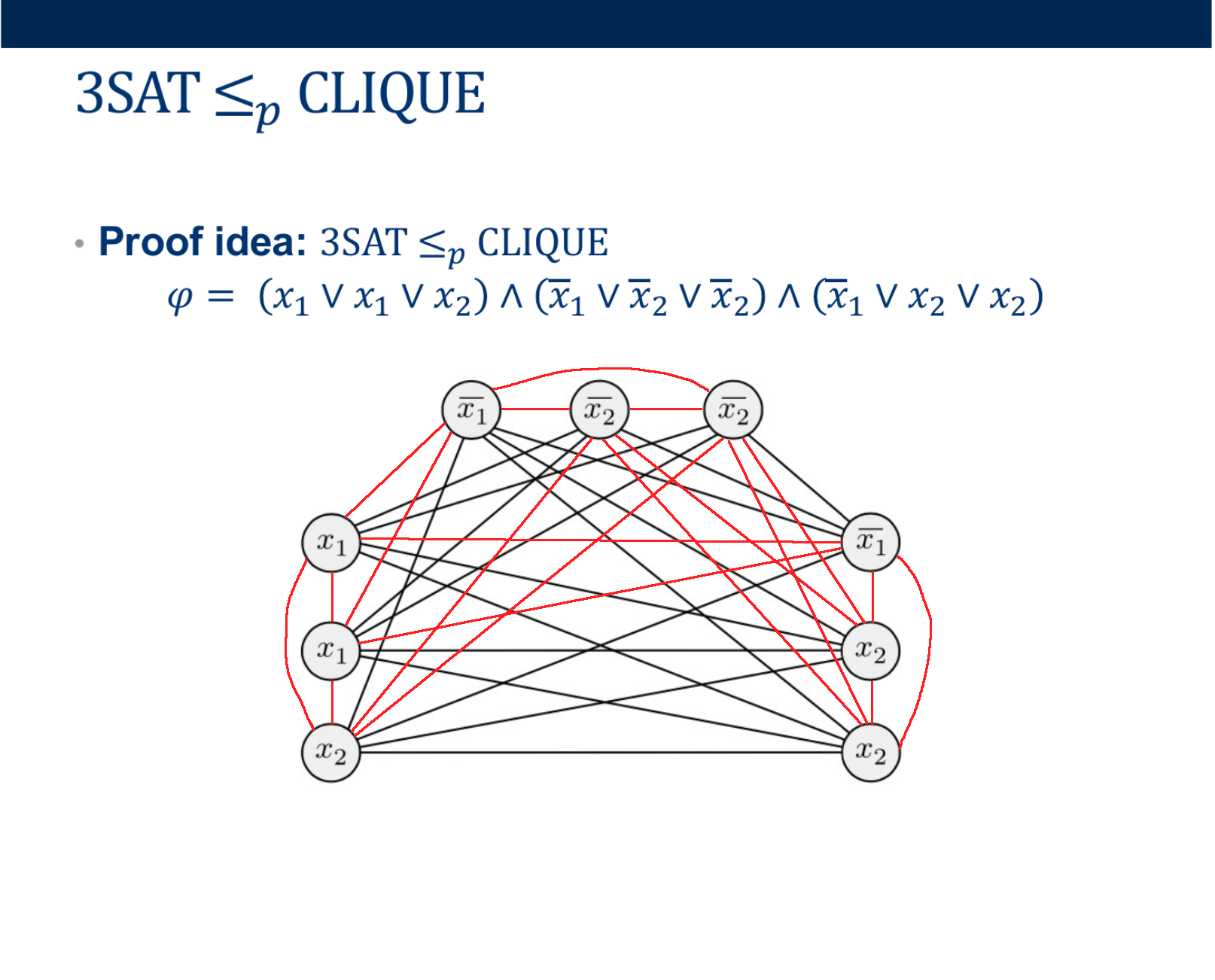
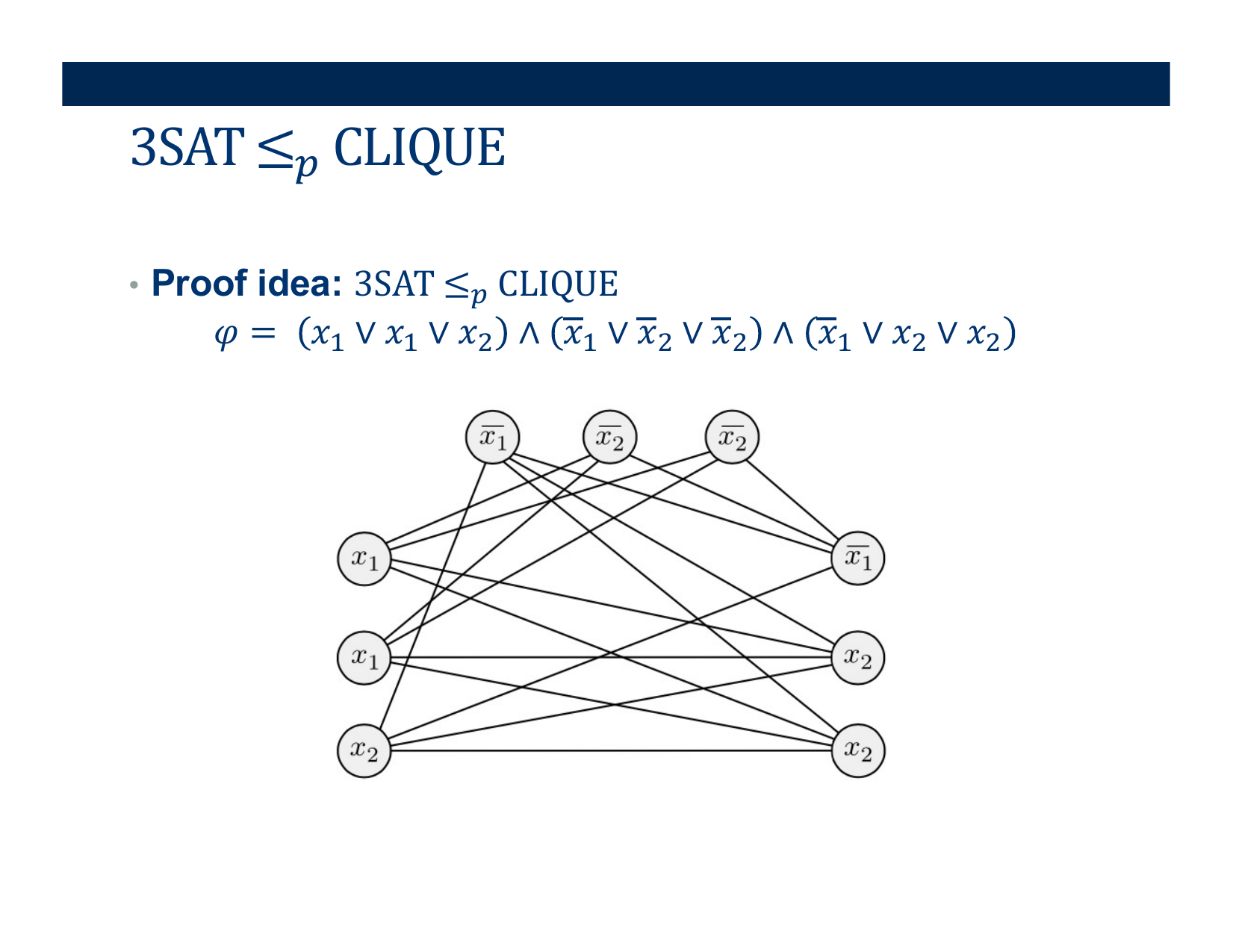
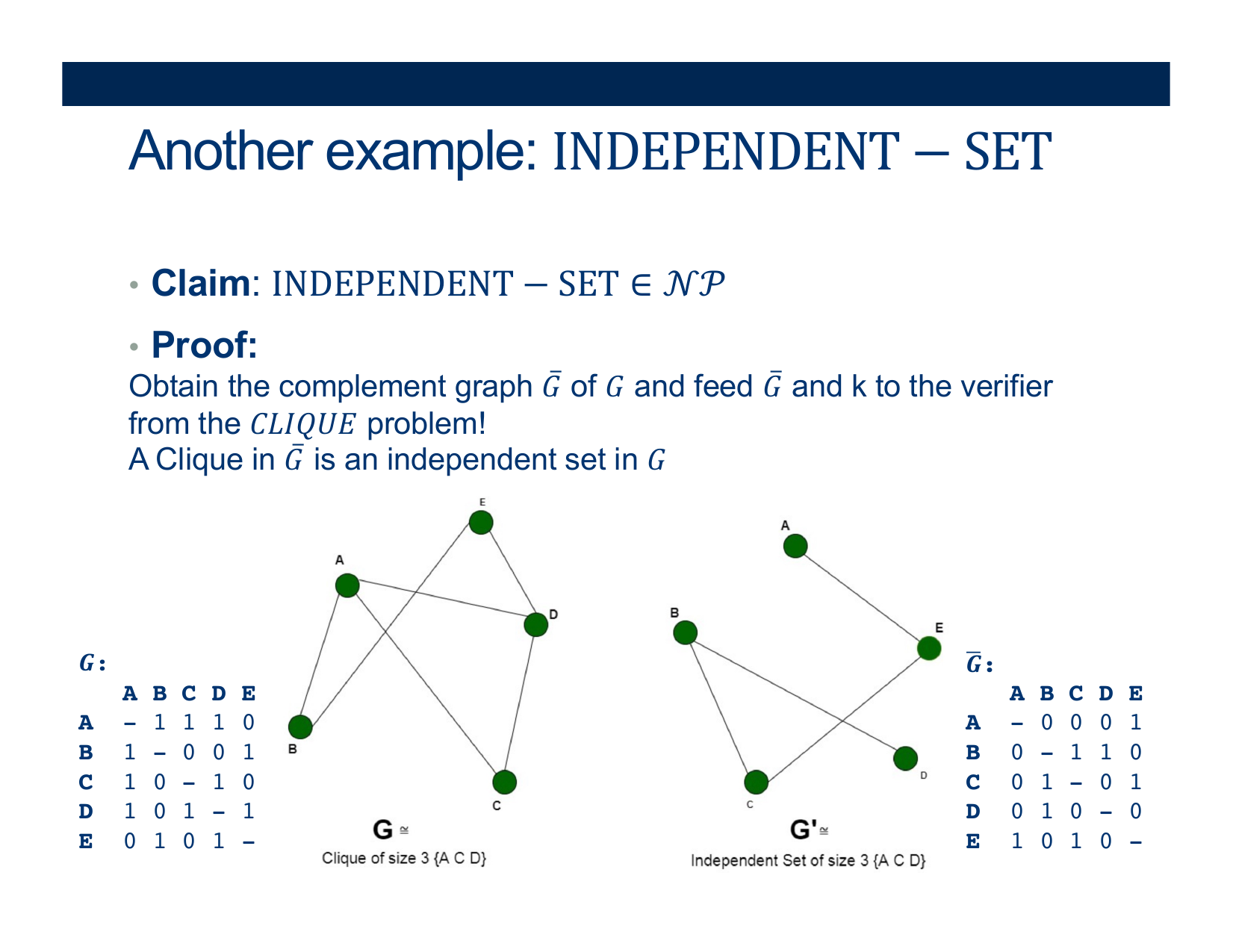
- Deciding if \( < G, k> \) belongs in CLIQUE
- Deciding if \( < G, k> \) belongs in Independent-Set





 TIP:
TIP:
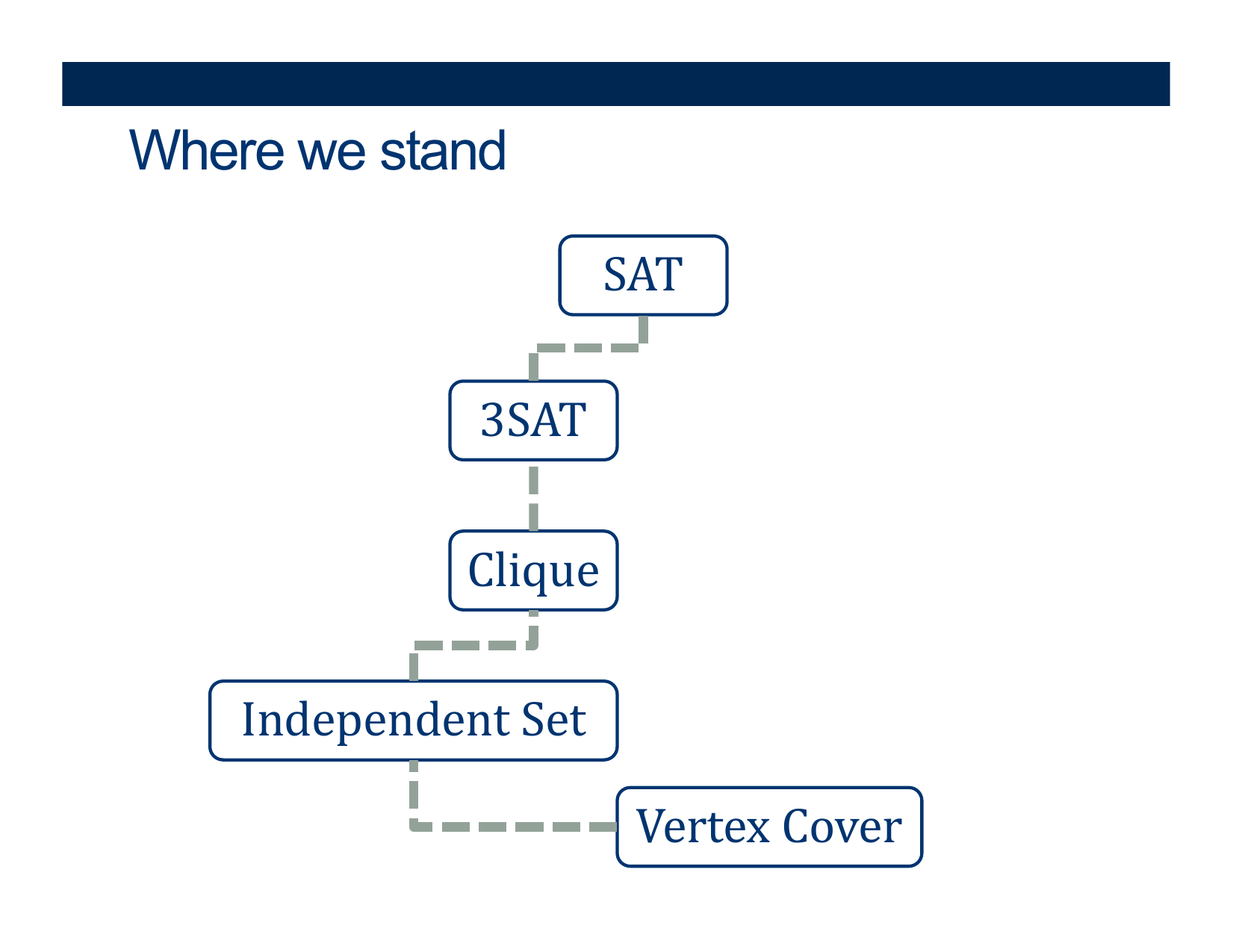
What is the most obvious vertex-cover of a graph \(G\>)?
What is the most obvious independent-set of a graph \(G\>)?
As you make the I-Set greater... what happens to the vertex-cover?
Is there a maximum I-Set in a graph \(G\>)?
What is the relation with the vertex-cover of a graph \(G\>)?
Activity [2 minutes] How would you Prove this?:
(Wait; then Click)


Upshot:
The largest I-Set must have, as its complement, the smallest vertex-cover!

Before next class (Wednesday 12/08)
[Due for everyone]
TODO
Review Decidable langs, Undecidable Langs, Un-recognizable Langs, Reductions (T, M), P, NP, NP-Hard, and NP-C, and P-Reductions.
[Optional]
TODO