SmithLogo

CSC 250

Theory of Computation

Smith Computer Science



Lecture Notes 30: More About Computational Complexity


Outline

This class we'll discuss:

Time Complexity Classes





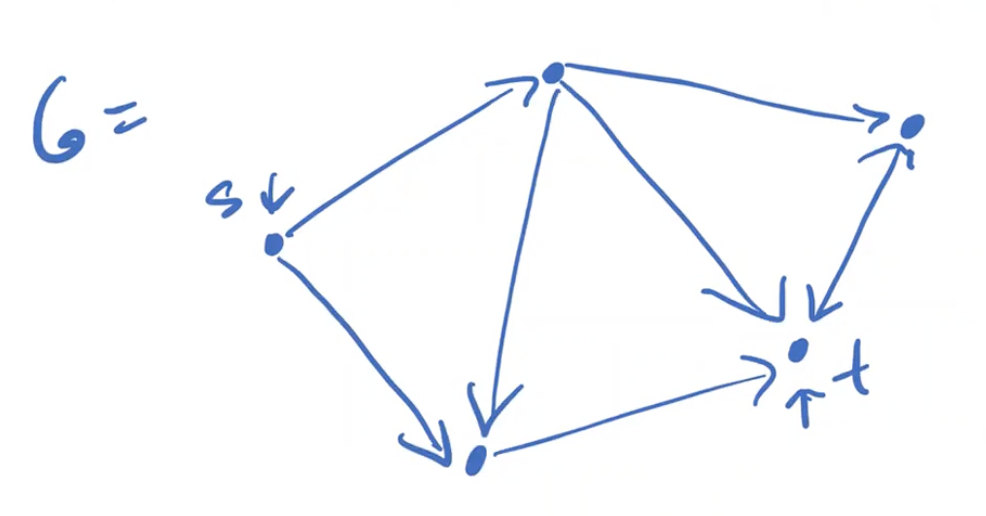
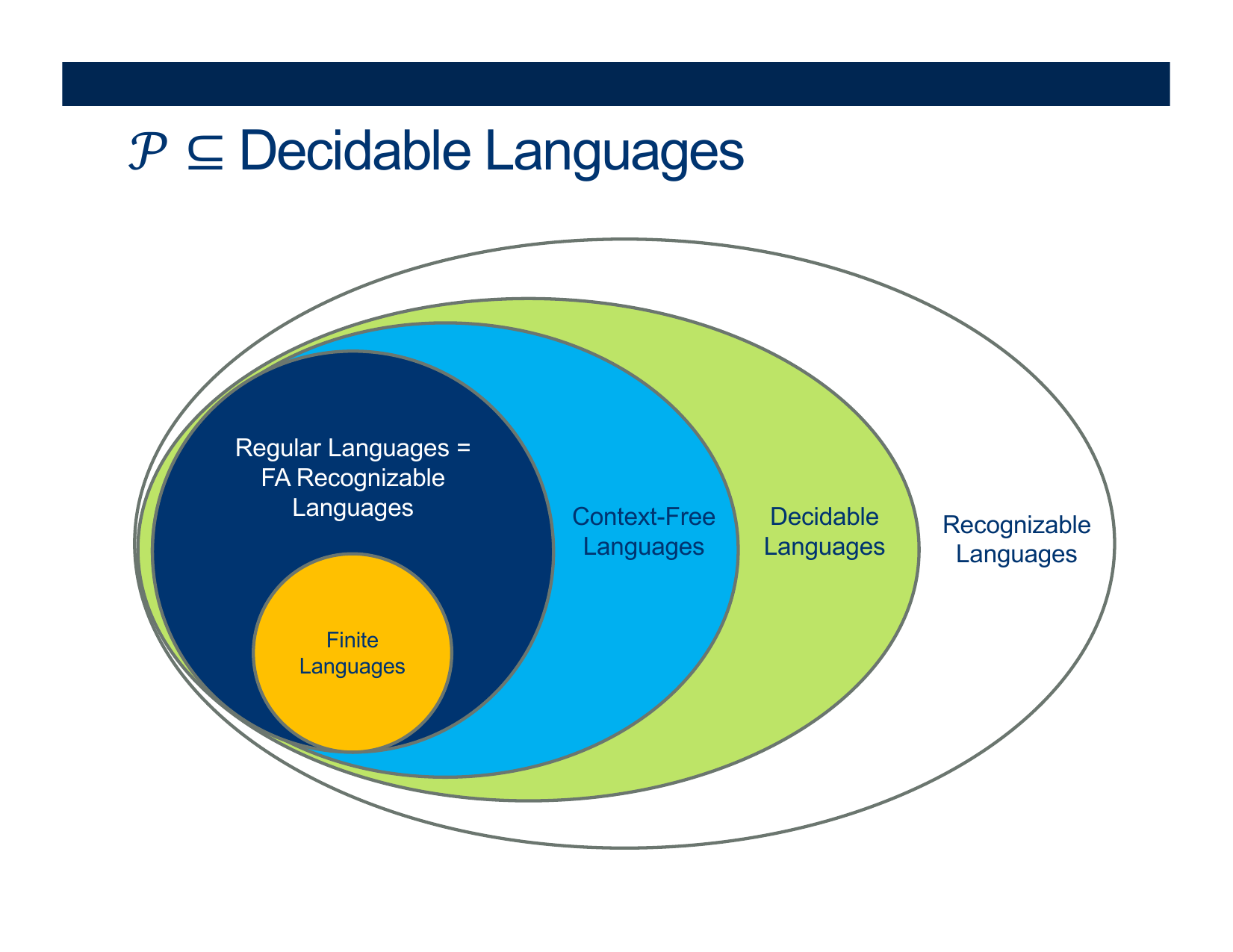
Some Typical Classes



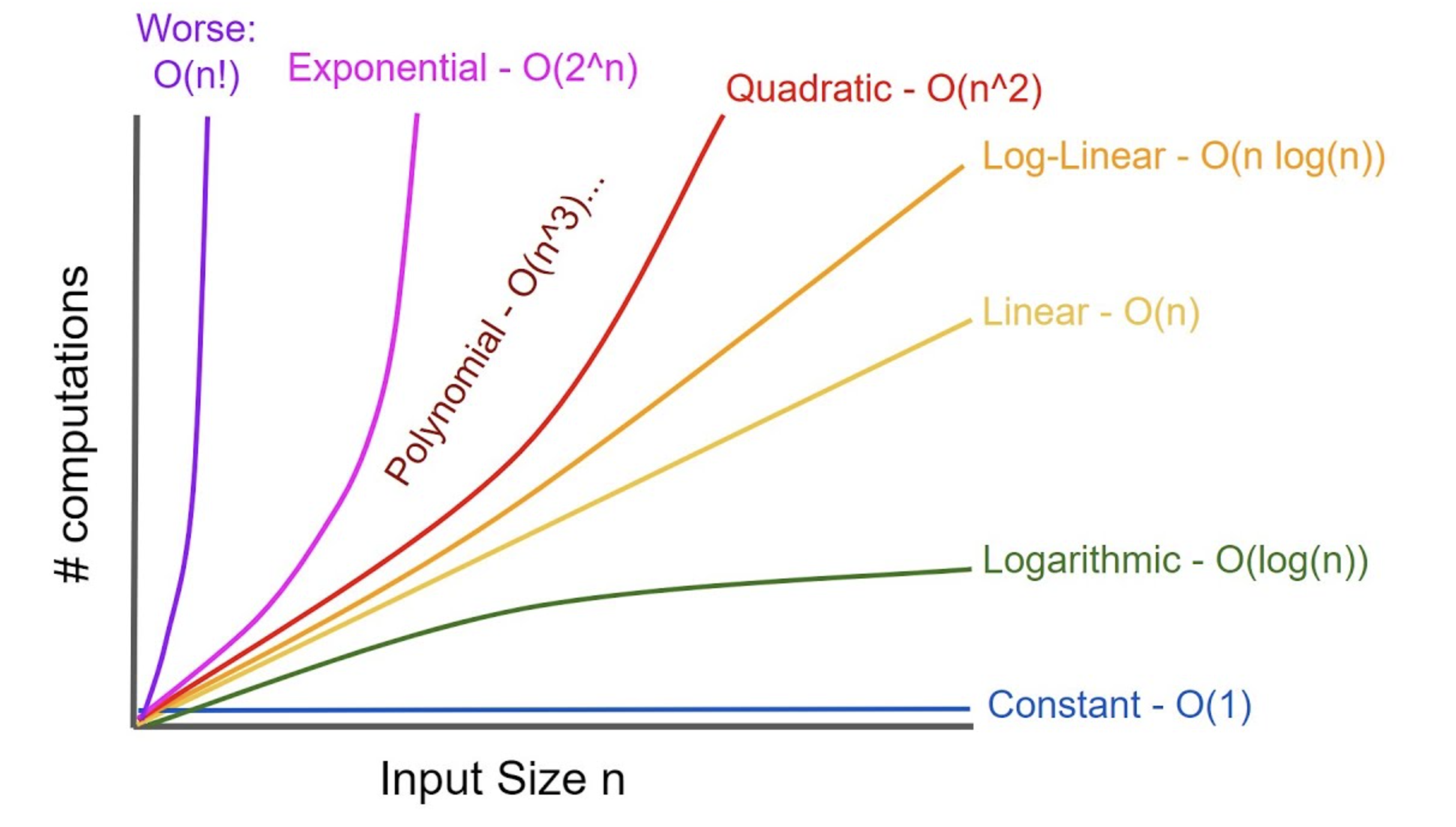
Check out examples Here







Activity 1 [2 minutes] How would you do this faster?:
(Wait; then Click)

 Also...What complexity is this?








Activity 2 [2 minutes] Is PALINDROME in O(n2)?:
(Wait; then Click)

 Also...What complexity is this?




Example:

SEL = {<M, A> | M sorts integer array A using SELECTION-SORT }



Activity 3 [2 minutes] Is SEL in O(n2)?:
(Wait; then Click)

 First: Build an algorithm that solves this in O(n2)... (this would mean YES!)
THEN, you may ask if SEL might belong to a lower complexity class ... (don't try...yet)












This is an example <G,s,t>∈PATH



Activity 4 [2 minutes] How would you Prove this?:
(Wait; then Click)

 You must build a Decider that solves it in O(nk) (Polynomial time)

Use Breadth-First-Search!
  1. On input <G,s,t>
  2. Mark all nodes rechable from the current node (starting at s and moving to the next in a running queue)
  3. Continue to expand until we reach t or ∄ another node
  4.   if we reach t : ACCEPT
  5. REJECT


What is the complexity!!!???

Complexity analysis:
Worst case: traversing every edge.
How many edges? ...

Another approach:
At most ∣V∣ phases are executed.
Each phase takes polynomial time to explore marked nodes and their outgoing edges.
(Imagine ∣V∣ nodes in a straight line VS ∣V∣ nodes all connected to each other)




















Activity 5 [2 minutes] How would you Prove this?:
(Wait; then Click)

 AutoTM_t = { |M| is a TM that accepts in ≤ t(|M|) steps }

Claim 1: AutoTM_t is decidable

Proof of Claim 1:
On input , simulate M on for t(|M|) simulated steps ADWID.



Claim 2: AutoTM_t can’t be decided by any basic TM in ≤ t(n) steps
Proof of claim 2: (everyone’s favorite contradiction argument)
Assume AutoTM_t is decided in time ≤ t(n) by some TM MA
This implies that the complement is also decided by some other TM MA― (just swap the accepting and rejecting states of MA )



Thus, for every Turing machine M:

<M> ∈ AutoTMt― iff MA― accepts in time ≤ t(|M|)
And by taking the complement of the definition of AutoTM_t:

<M> ∈ AutoTMt iff MA― does not accept <M> in time ≤ t(|M|).

What happens if we plug in MA― for M in both statements: MA― ∈ AutoTMt― iff MA― accepts in time ≤ t(|MA―|)
MA― ∈ AutoTM_tc iff MA― does not accept in time ≤ t(|M|).

– Contradiction!


















Homework


[Due for everyone]
TODO

[Optional]
TODO