SmithLogo

CSC 250

Theory of Computation

Smith Computer Science



Lecture Notes 25: Mapping Reducibility


Outline

This class we'll discuss:



Recap: Reductions





























Activity 1 [2 minutes] How would you do this reduction?:
(Wait; then Click)













Activity 2 [2 minutes] How would you do this reduction?:
(Wait; then Click)

Assume EQTM is decidable, and so there exists some \(D_{EQTM}\) that decides, for any input \(< M_1, M_2>\), whether \(M_1\) Accepts the same language as \(M_2\).

We'll design the Machine \(D_{EmptyTM} \) as follows:

\[ \begin{align*} &D_{EmptyTM}:\\ & \text{ On input $ < M > $ }:\\ & \text{ Create (but don't run) $HELPER_{\emptyset}$ such that}\\ & \quad \text{ On input $ < X > $ }:\\ & \quad \quad \text{ Ignore $ < X > $ }\\ & \quad \quad \text{ Reject}\\ & \text{ Now Run $D_{EQTM}$ on input $ < M, HELPER_{\emptyset} $ ADWID}\\ & \text{ If $D_{EQTM}$ accepts, it is only because M accepts no words so our machine ACCEPTS}\\ & \text{ If $D_{EQTM}$ rejects, , it is only because M accepts some w so our machine REJECTS}\\ \end{align*} \]













Activity 3 [2 minutes] How would you do this reduction?:
(Wait; then Click)

  • Reject if: \(D_{EMPTY}\) accepts \(M_{M,w}\)
  • Accept if: \(D_{EMPTY}\) rejects \(M_{M,w}\)
    •


























    The Emptiness Problem

  • Theorem: \(\overline{EMPTY-TM}\) is recognizable
  • Theorem: \(EMPTY-TM\) is undecidable
  • Corollary: \(EMPTY-TM\)is unrecognizable
  • Proof: If \(\overline{EMPTY-TM}\) and \(EMPTY-TM\) recognizable,
  • that would imply \(EMPTY-TM\) is decidable




    • This means our Turing Reduction Can't catch if the fact that we're reducing outside the same class of languages

    Issue with EMPTY ≤ ¬EMPTY is that the “Domain” of one is complement of the “Domain” of the other!



    However, we've actually seen a STRONGER type of reduction





    Here, The “Domain” of EMPTY corresponds to the “Domain” of EQ!







    We could rewrite this as a simple conversion from any word in EmptyTM to a word in EQ_TM (and similarly a word not in EmptyTM to a word not in EQ_TM).

    We call this a mapping reduction, and denote it \( \leq_m\)



    Mapping Reductions

























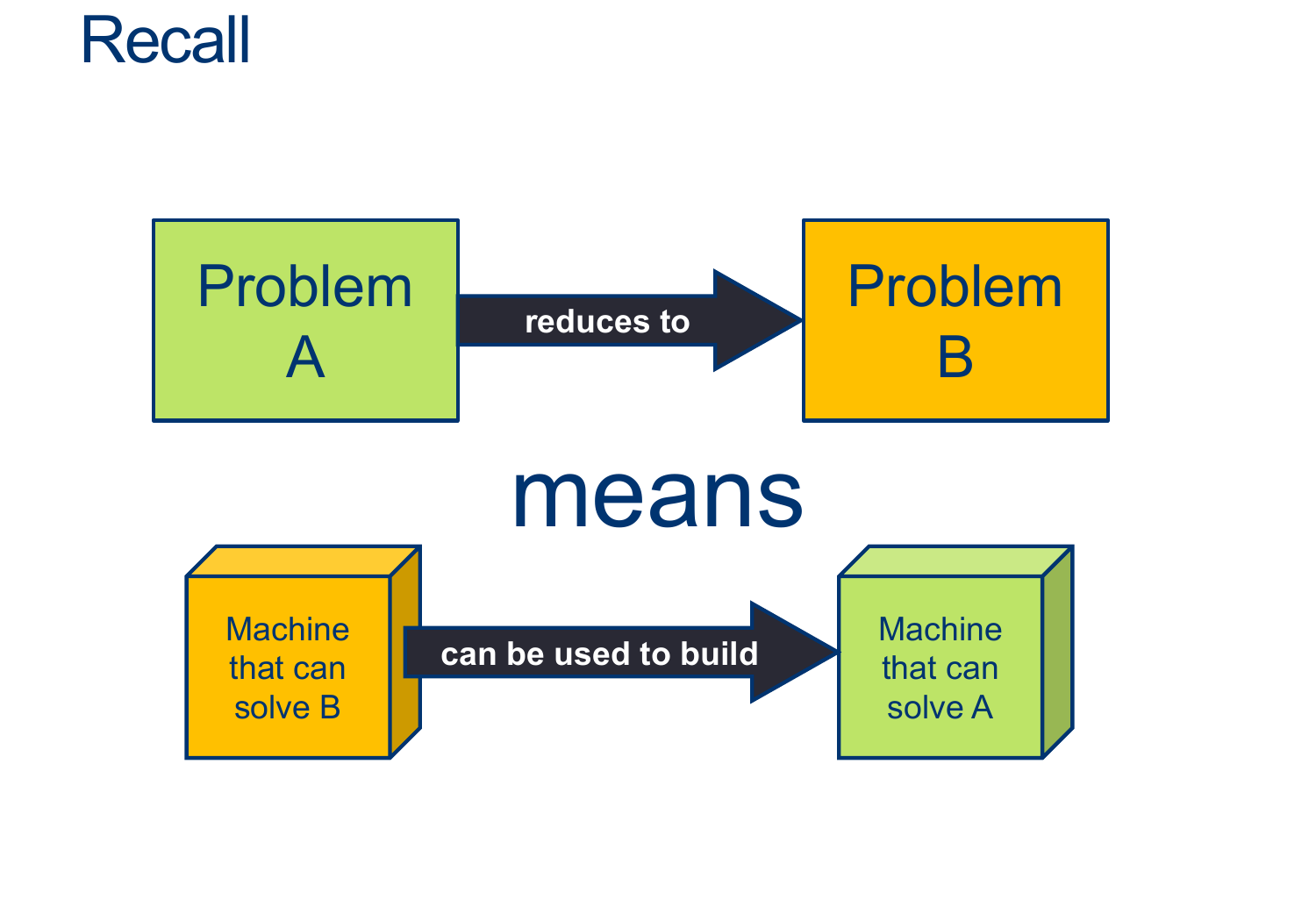
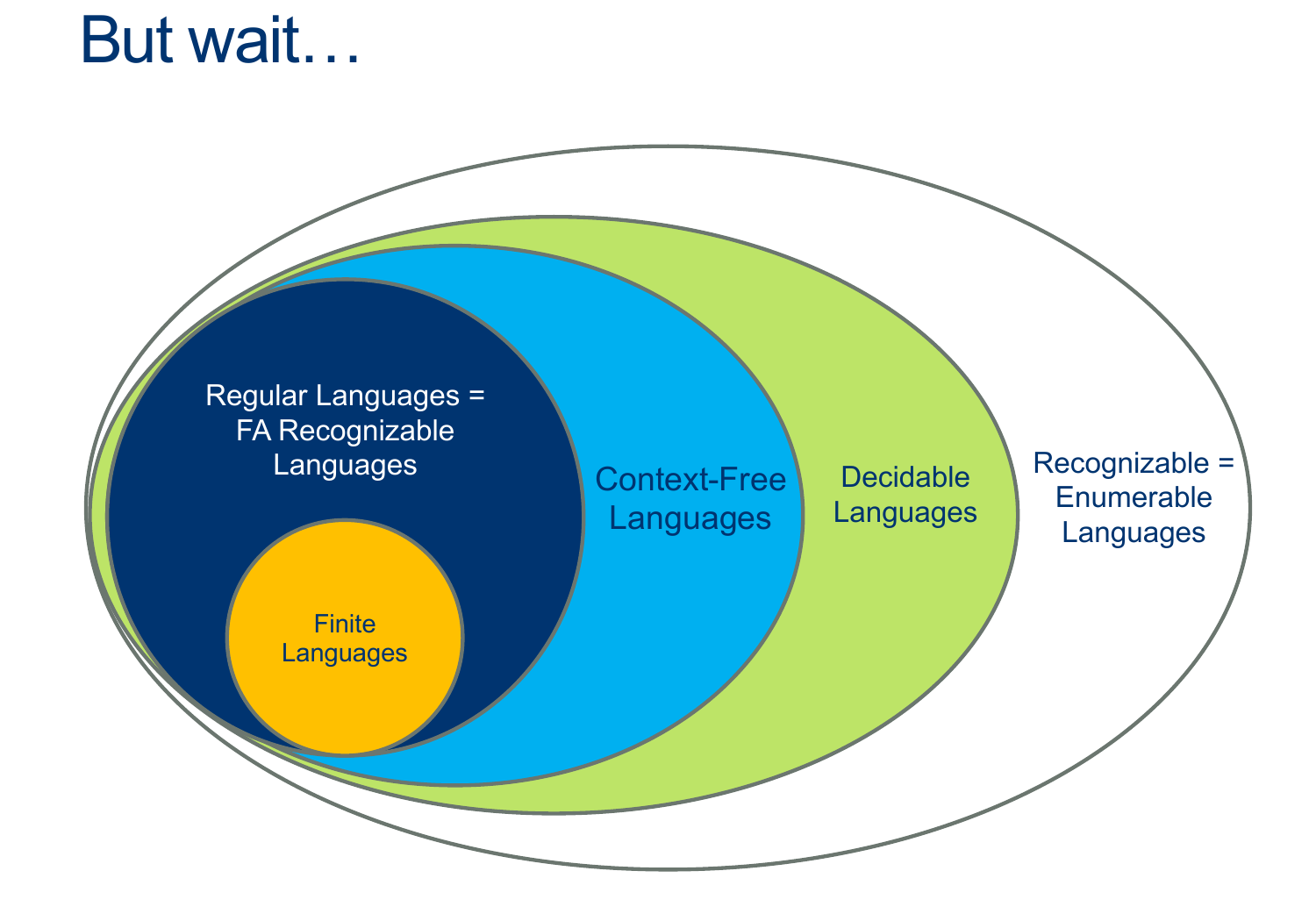
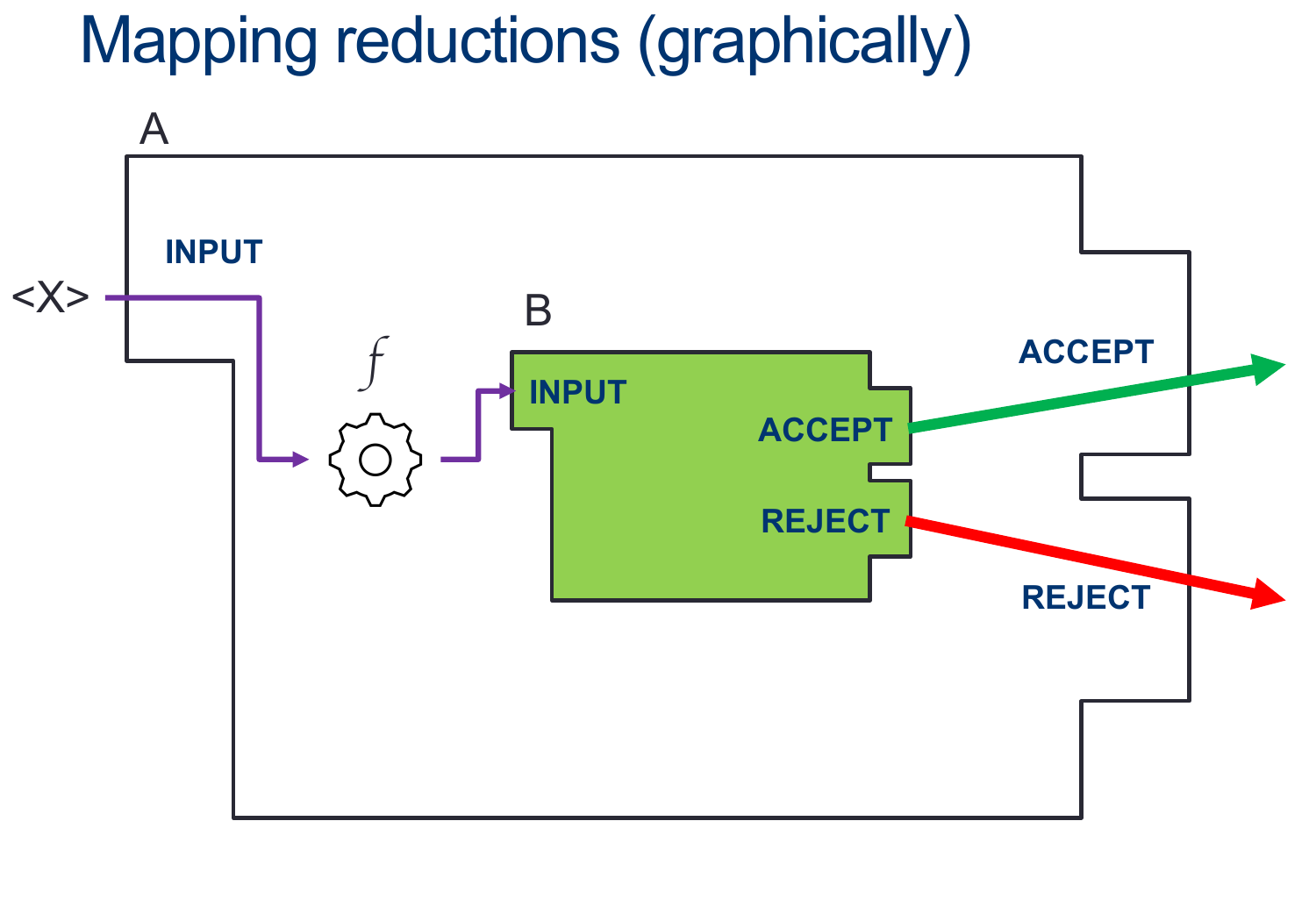
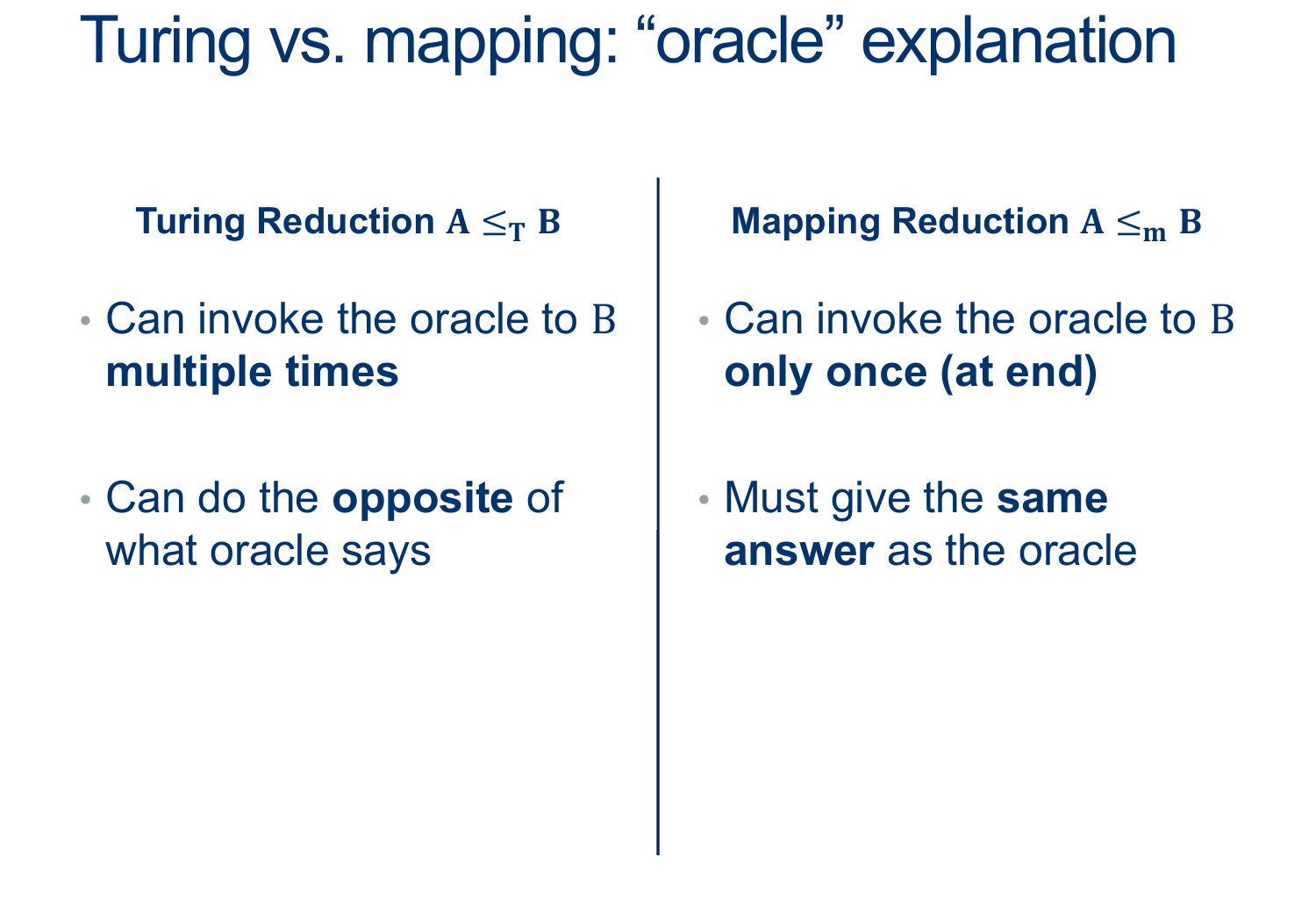
    They’re a way for us to relate problems to one another
    If A reduces to B and B is easy => A is easy too
    More common: if A reduces to be and A is hard => B is hard too

    We started with ATM (which we proved was undecidable using a big ugly contradiction )
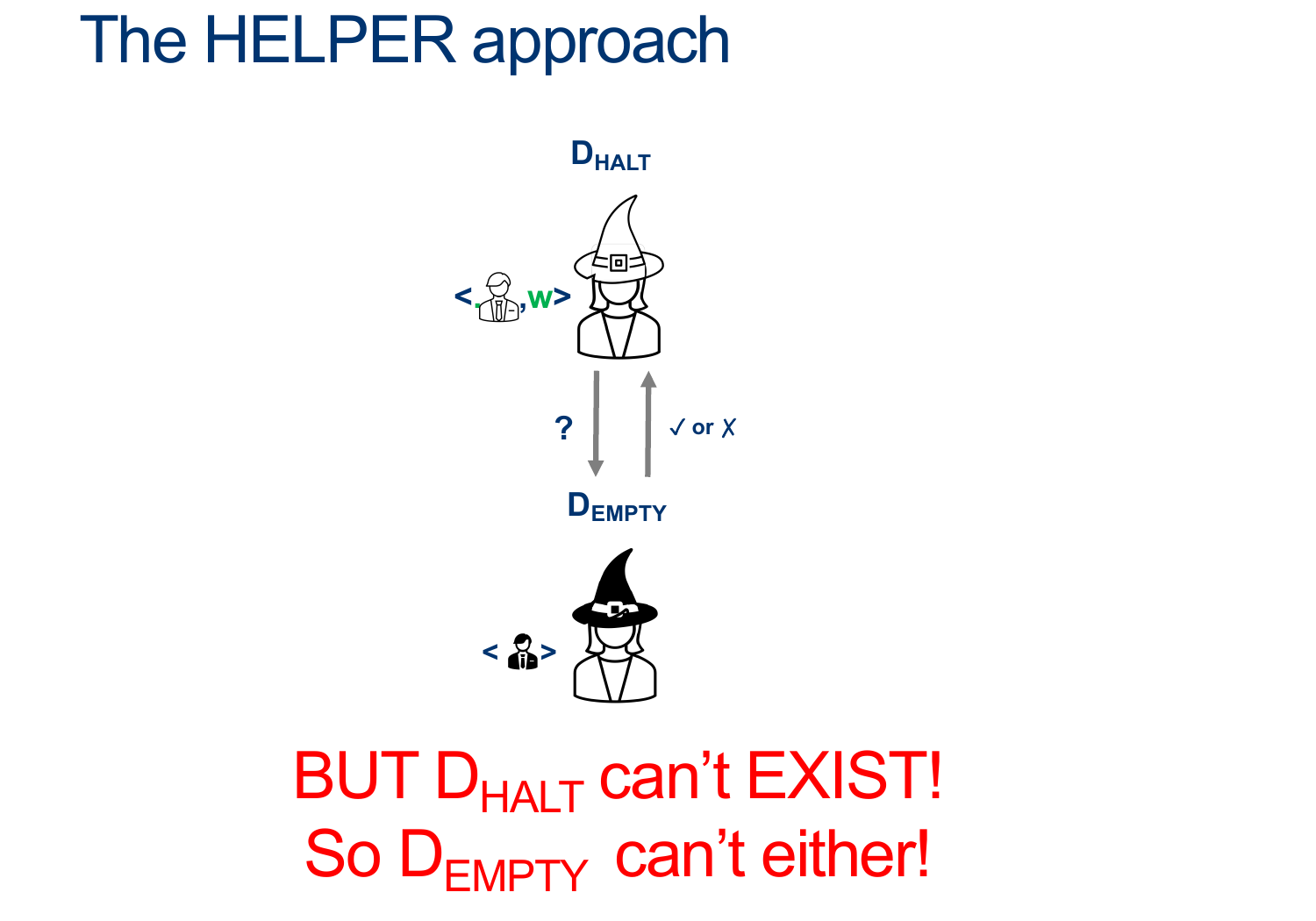
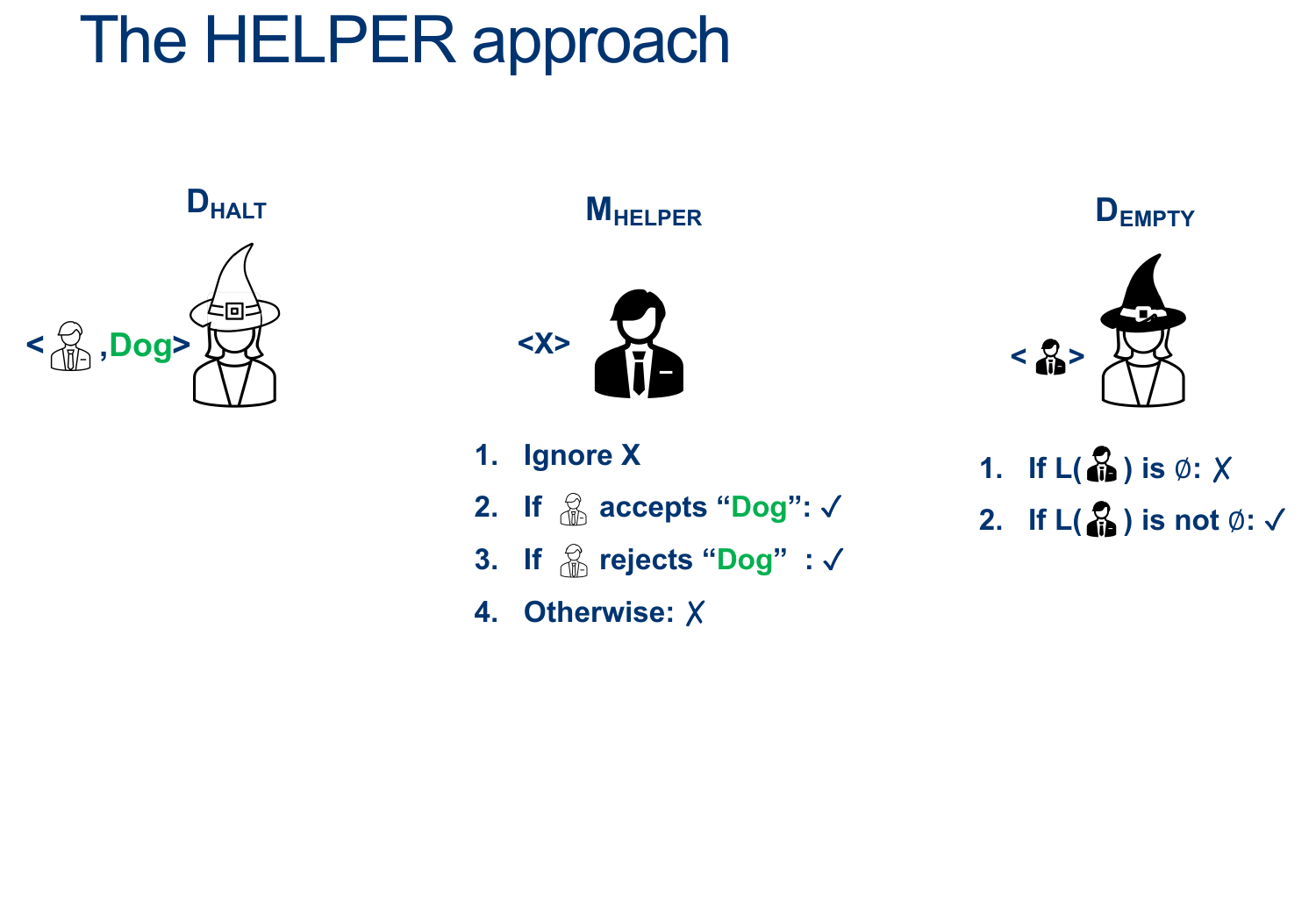
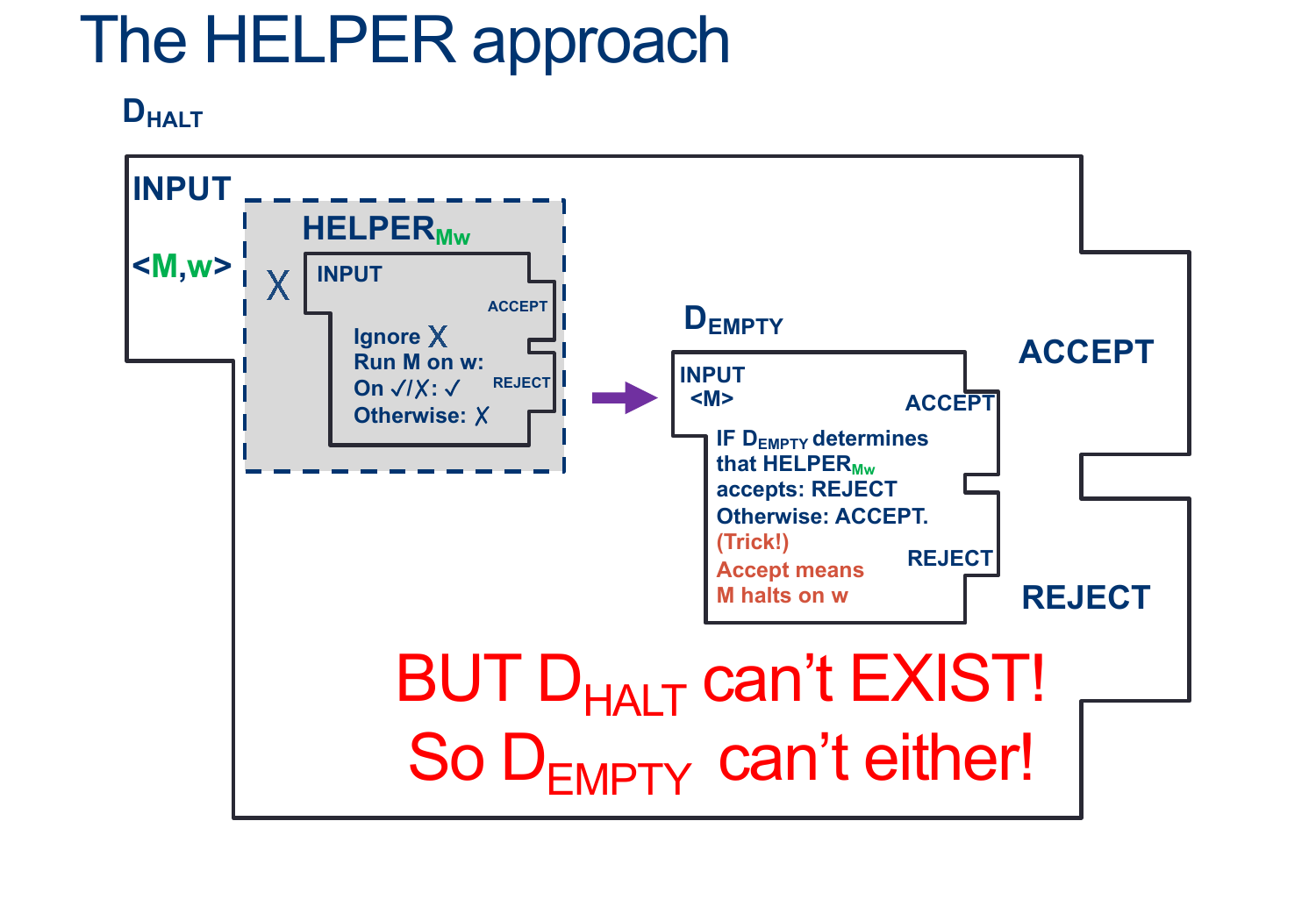
    Reduced ATM to HALT (ATM ≤ HALT): we showed that if we had a decider HALT, we could use that to decide ATM (so that means HALT must also be undecidable)

    We did the same thing with ATM-01
    And EmptyTM
    Later, we also showed that if we had a decider for HALT, we could use that to decide EmptyTM
    And that if we had a decider for EQ_TM, we could yet again decide EmptyTM (mapping)













    Next: Rice's Theorem



    Homework


    [Due for everyone]
    Review reductions and mapping reductions (video and recorded lectures)
    PS07 will be out tonight Due Next Friday (with auto-extension until Monday 04/11)

    [Optional]
    TODO