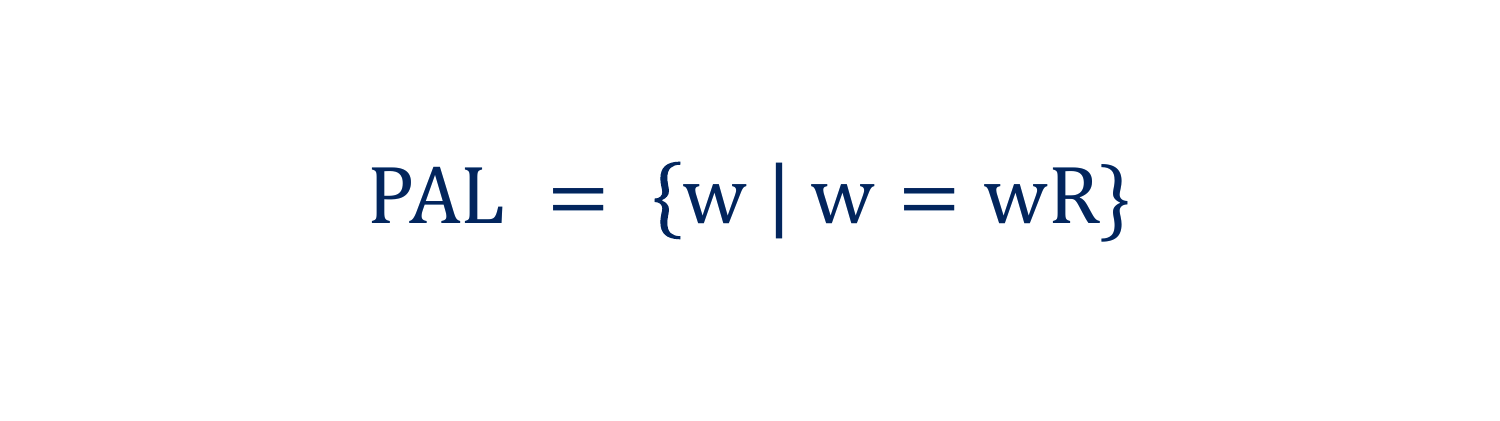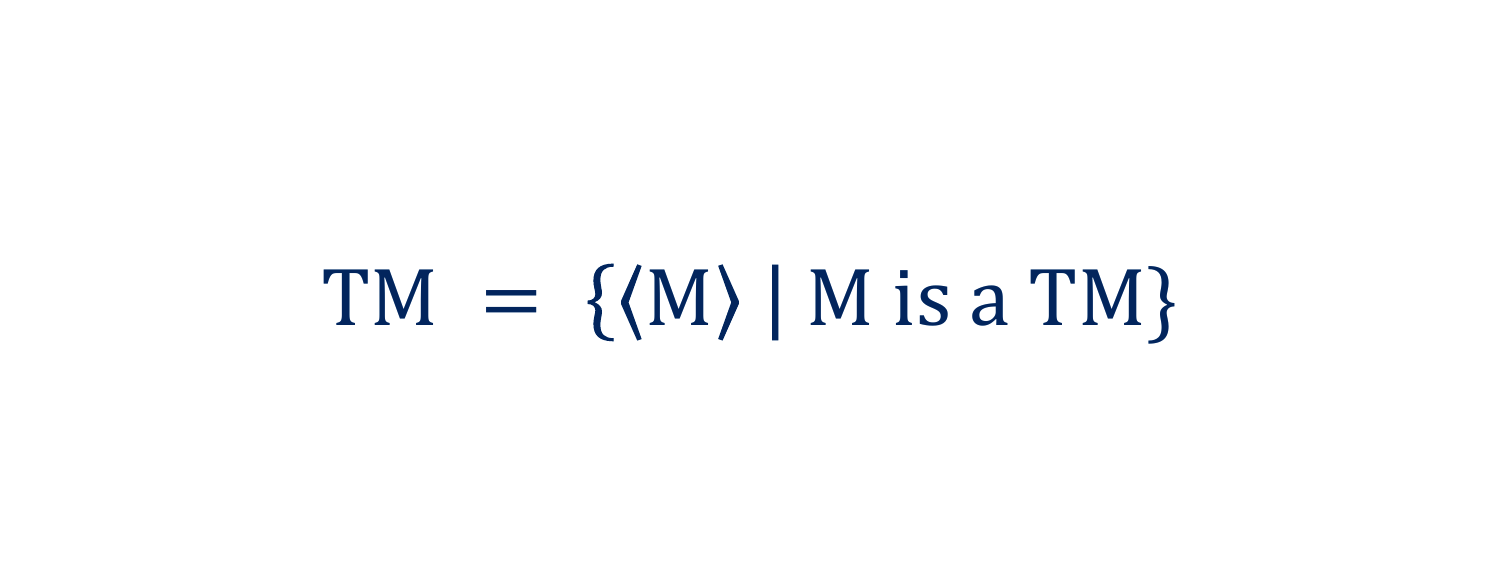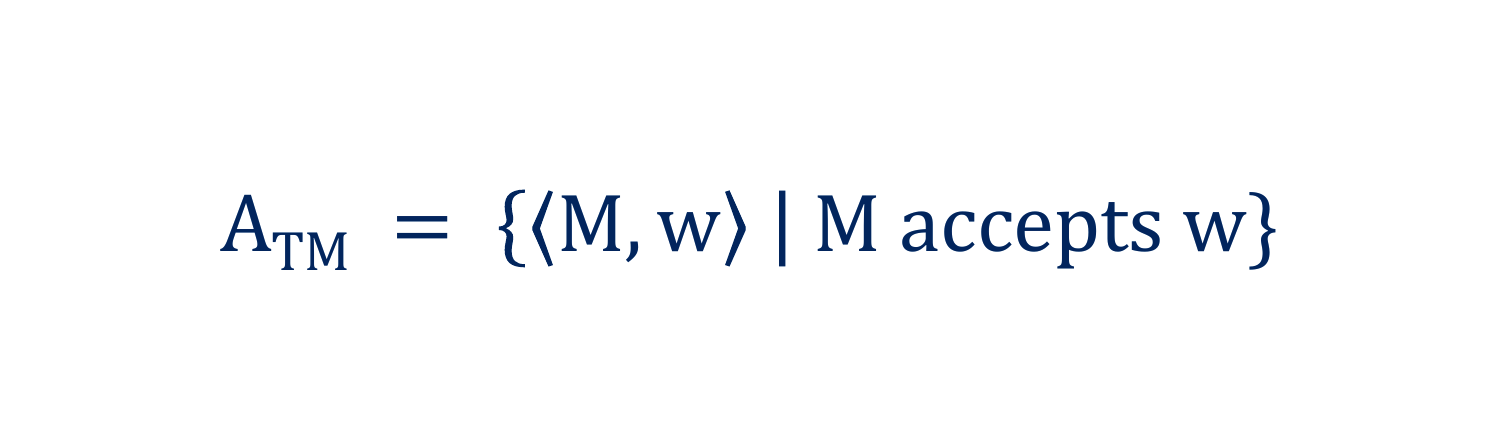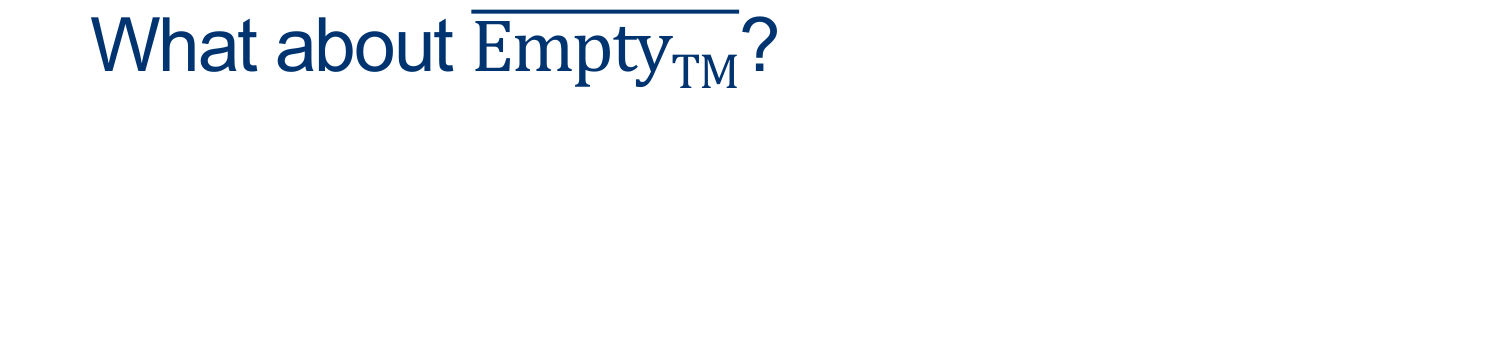SmithLogo

CSC 250

Theory of Computation

Smith Computer Science



Lecture Notes 23: Revisiting Reductions


Outline

This class we'll discuss:



Recap: Terminology



The following are examples of Languages:
















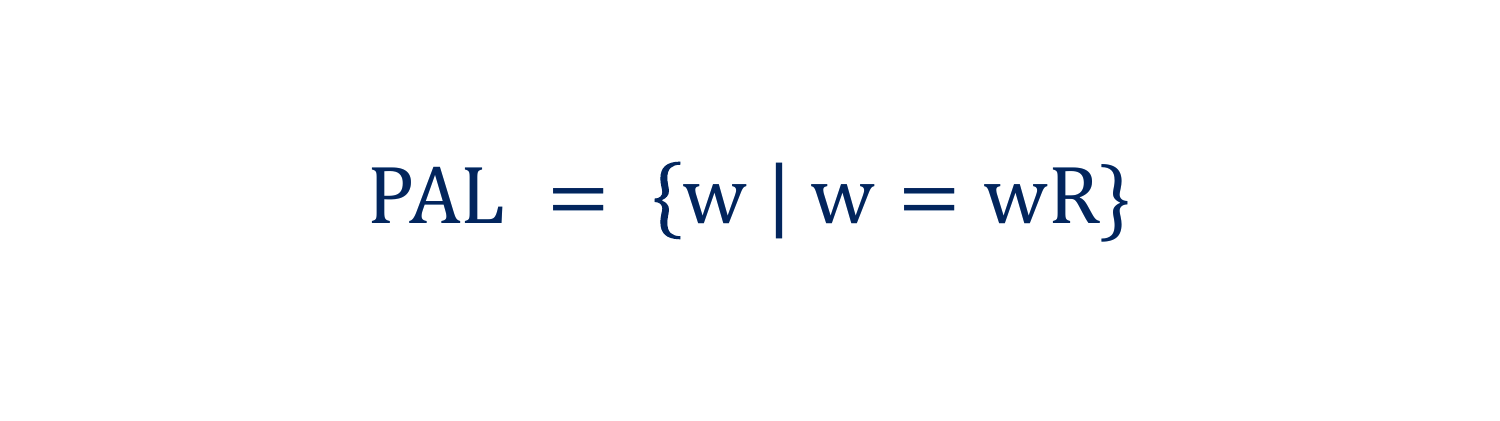
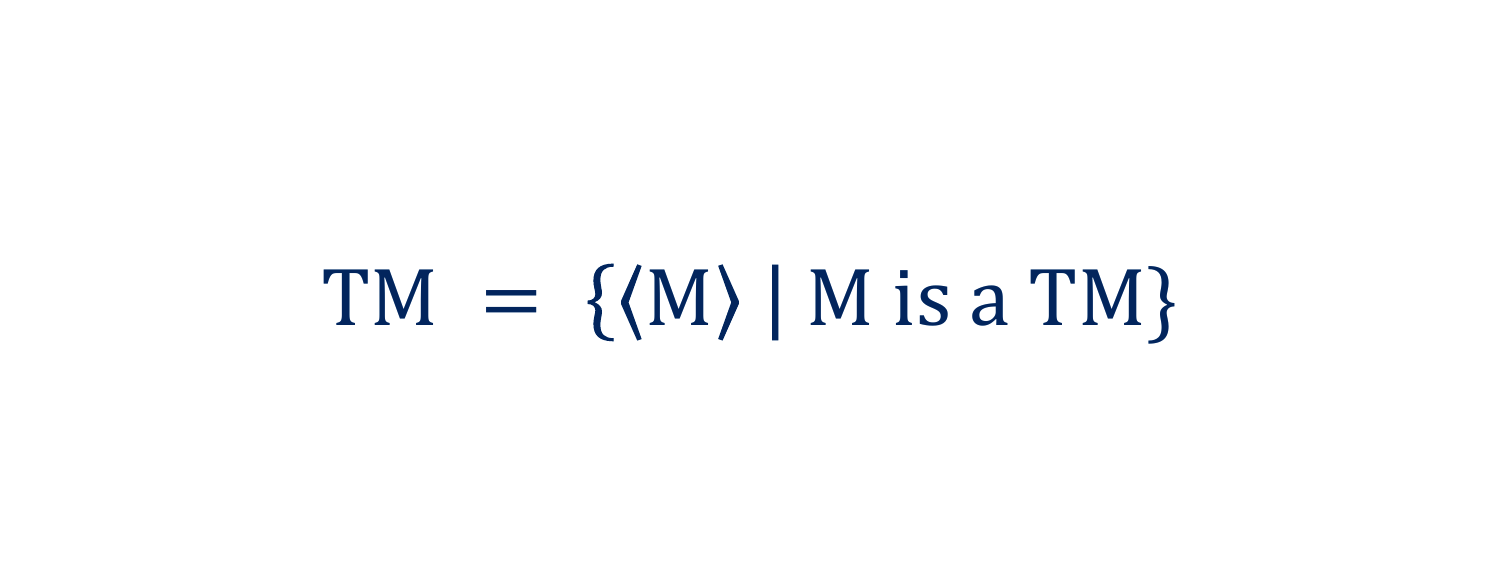
They have varying degrees of complexity in the patterns that make up the words.
But, in the end, these are simly all just sets of words.



Where we left off...







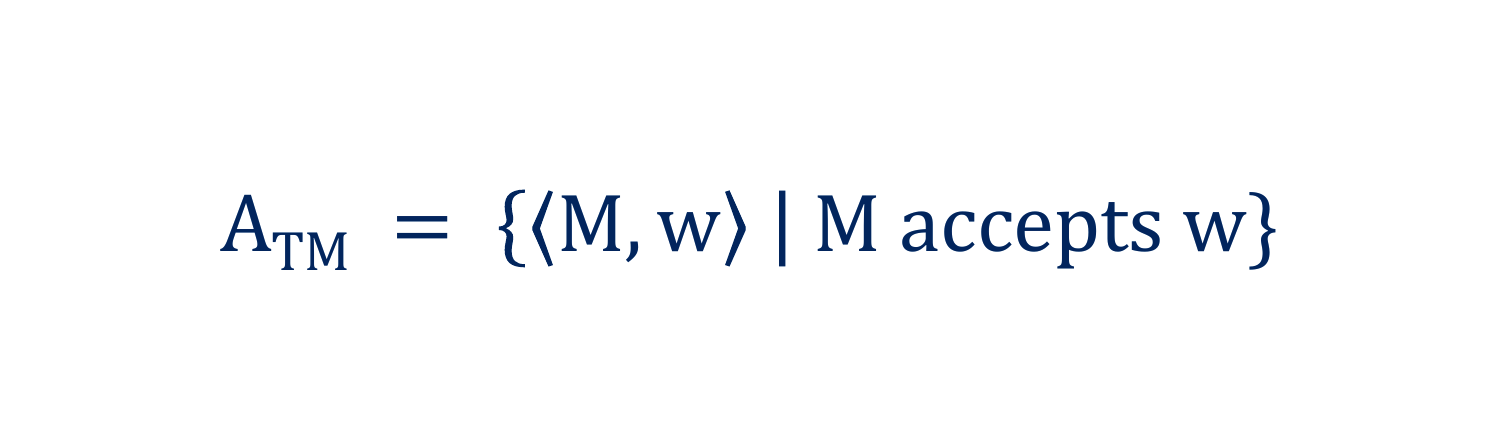
Remember, We can define TMs using Pseudocode!

Activity 1 [2 minutes]:
In teams, write a Machine that generates the language \(L_1\) shown above.
(Wait; then Click)



Is this a Recognizer or a Decider?




Is that the only machine that Decides \(L_1\)?.
(Wait; then Click)









Machines with infinite languages

Activity 2 [2 minutes]:
In teams, write a Machine that generates the language \(L_2\) shown above.
(Wait; then Click)







More Machines with infinite languages

Activity 3 [2 minutes]:
In teams, write a Machine that generates the language \(PAL\) shown above.
(Wait; then Click)



















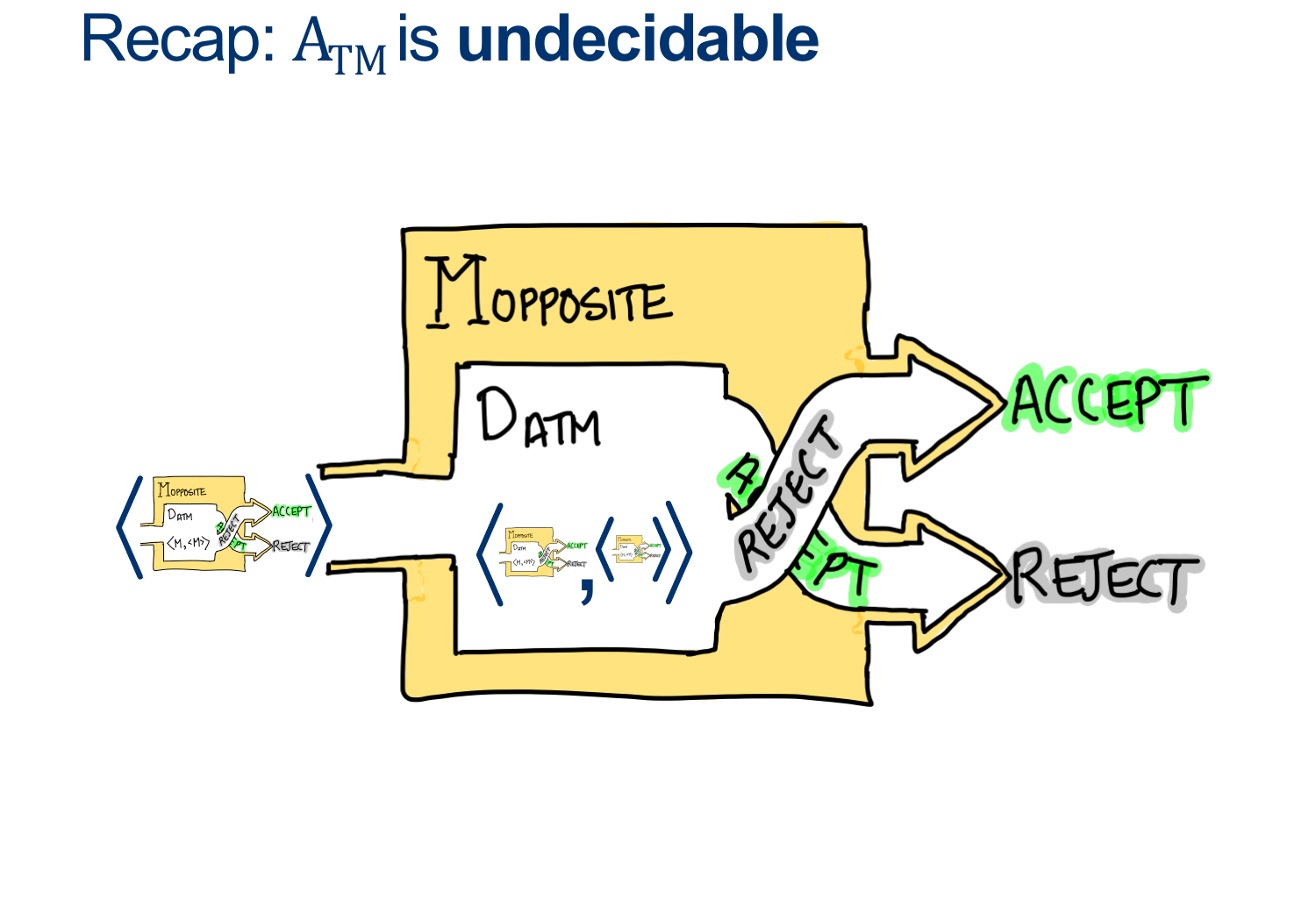
Recap: Is ATM is UNdecidable

We proved this by Contradiction.
We assumed ATM was decidable and built a helper machine to arrive at a contradiction:


Consider the Machine \(M_{OPPOSITE} ( < M> )\)

\[ \begin{align*} &M_{OPPOSITE}:\\ & \text{ On input $ < M > $ }:\\ & \text{ Simulate $D_{ATM} \; on \; < M , < M > > $}\\ & \text{ If $D_{ATM}$ accepts, REJECT. }\\ & \text{ If $D_{ATM}$ rejects, ACCEPT. }\\ \end{align*} \]

Now, what happens when we run \(M_{OPPOSITE} ( < M_{OPPOSITE}> )\) ?






Using Reductions to prove Undecidability

  • A Reduction is a way to relate one problem A to another problem B so you can claim that:
    • If you can solve B, then you can solve A"
  • In this case, we know that problem A is Undecidable and we want to prove the same for B
  • We write it like this: \(A \leq B \)
  • This means: problem B is at least as hard as problem A
  • If we prove this, then we can say: since B is at least as hard as than A, and A is Undecidable, then B must be Undecidable as well!
  • The difficulty lies in relating of A to B

Example: Reducing ATM to HALT

Activity 3 [2 minutes]:
In teams, discuss how you would show that:
"If you could solve HALT, you could use it to solve ATM"


(Proof that ATM ≤ HALT)

In other words, \( HALT\) is AT LEAST as hard as \( ATM \)
(So if we can solve HALT, we can, for sure, solve ATM)



The Proof:

Assume HALT is decidable, and so there exists some \(D_{HALT}\) that decides, for any input \(< M,w>\), whether \(M\) halts on \(w\).

We'll design the Machine \(D_{ATM} \) as follows:

\[ \begin{align*} &D_{ATM}:\\ & \text{ On input $ < M, w > $ }:\\ & \text{ Simulate $D_{HALT} \; on \; < M, w > $}\\ & \text{ If $D_{HALT}$ rejects, $M$ doesn't halt, so it did not accept: REJECT. }\\ & \text{ If $D_{HALT}$ accepts, we know $M$ won't loop forever, so }\\ & \quad \text{ Simulate $M$ on $w$ ADWID }\\ \end{align*} \]

This machine is a decider for ATM (why?)
– it avoided the only problem we had with solving ATM, namely telling the difference between looping and lot waiting long enough.

However, we proved that ATM was undecidable by contradiction just a few minutes ago.
Aaaand...the only condition we need to build \(D_{ATM}\) was that \(D_{HALT}\) existed, so ...
\(D_{HALT} \; \) must not exist.











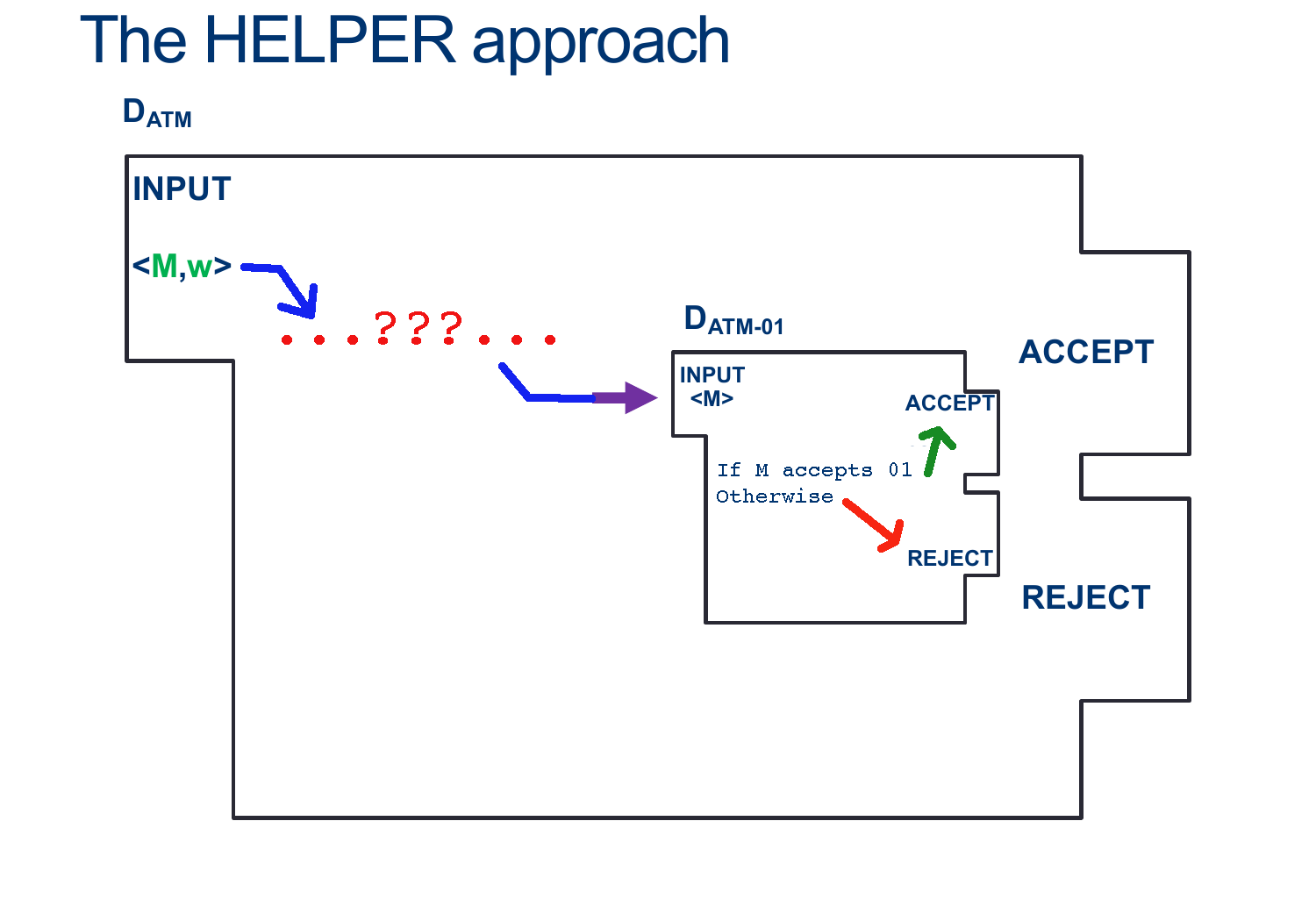
(ATM-01 is at least as hard to decide as ATM)

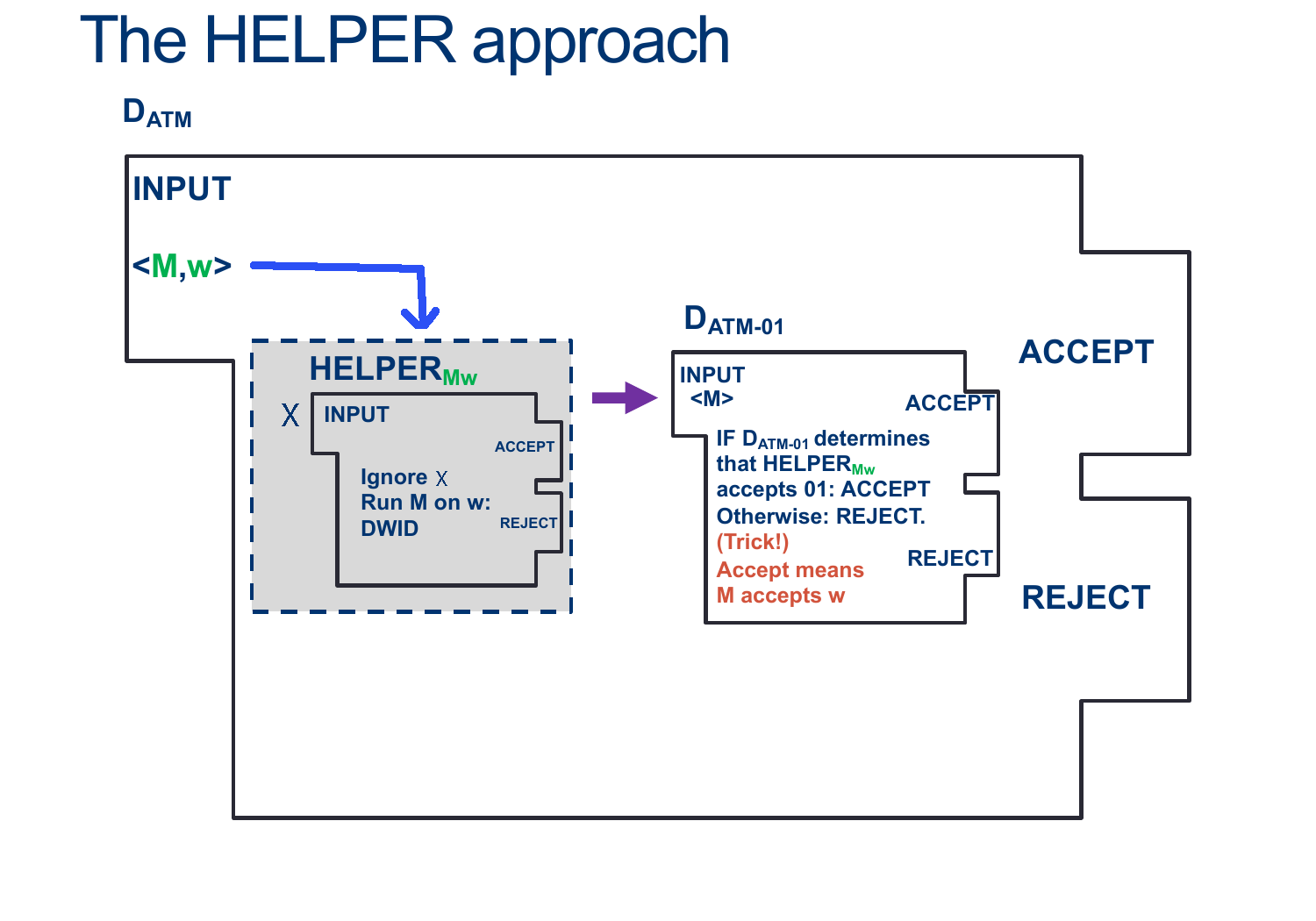
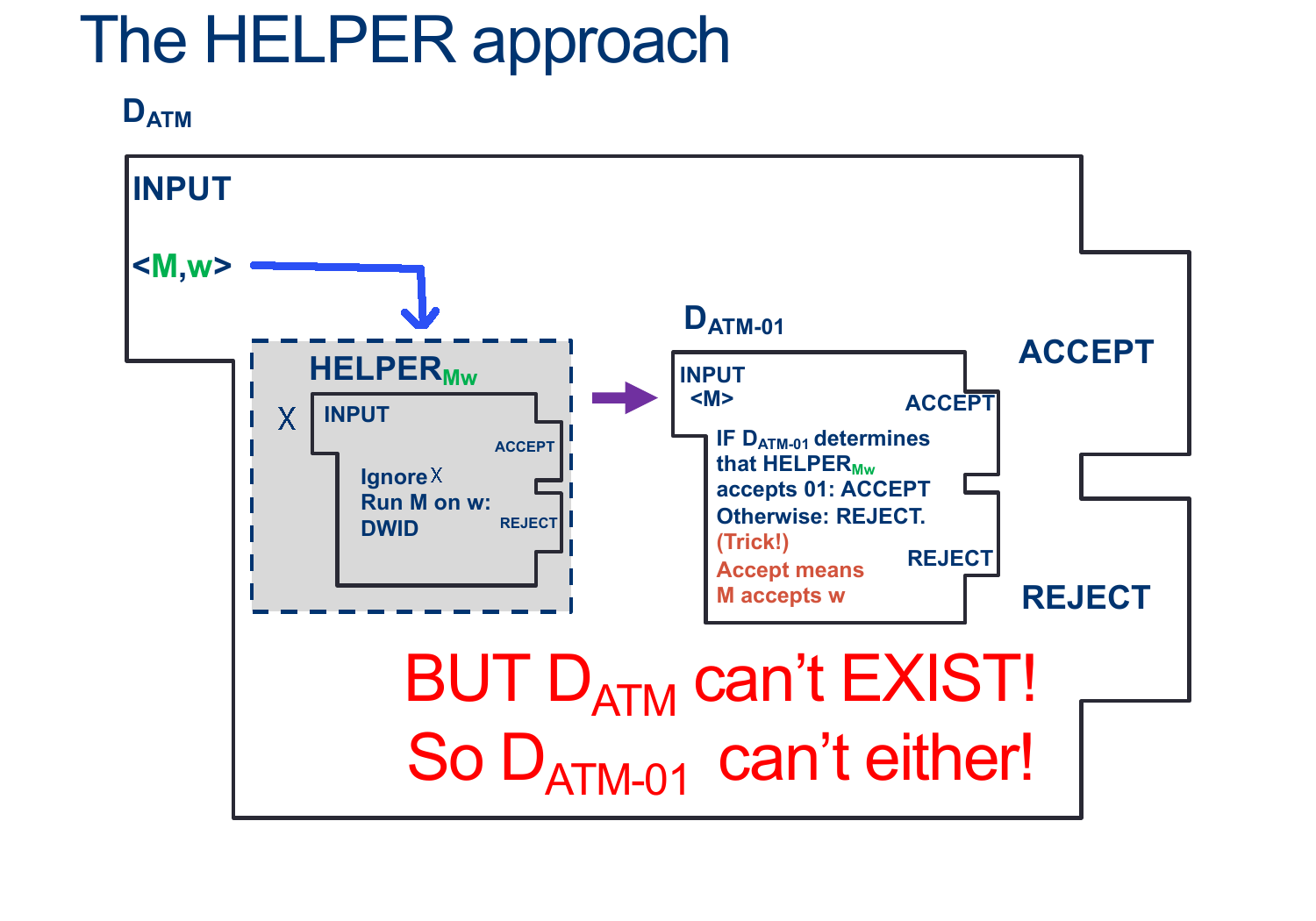
Note that:
  1. IF a machine \(D_{ATM}\) existed, it would receive input \( < M, w > \)
  2. IF a machine \(D_{ATM-01}\) existed, it would receive input \( < M > \)
  3. The order of the proof is:
    1. Assume \(D_{ATM-01}\) already exists
    2. We can use it to build another machine that should behave like \(D_{ATM}\)
    3. This larger machine, should be able to handle input \( < M, w > \)
    4. You must somehow get a machine with ONLY \( < M > \) as input to handle the input \( < M, w > \)
    5. Note that, as part of the steps, you can build helper machines





Activity 4 [2 minutes]:
In teams, write a Machine that uses \(D_{ATM-01}\) to perform the work of \(D_{ATM}\)
(Wait; then Click)



























This can be written like this:

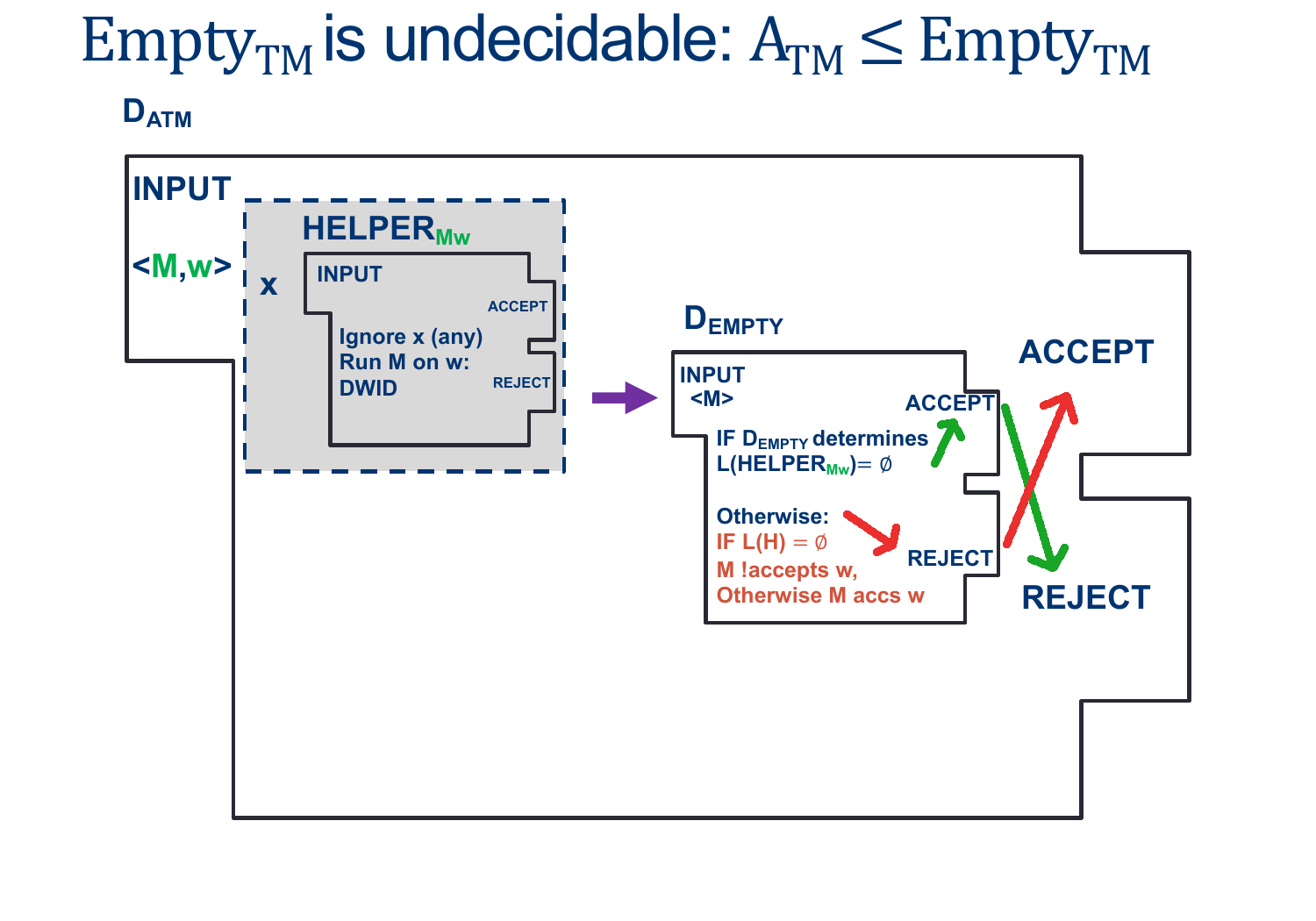
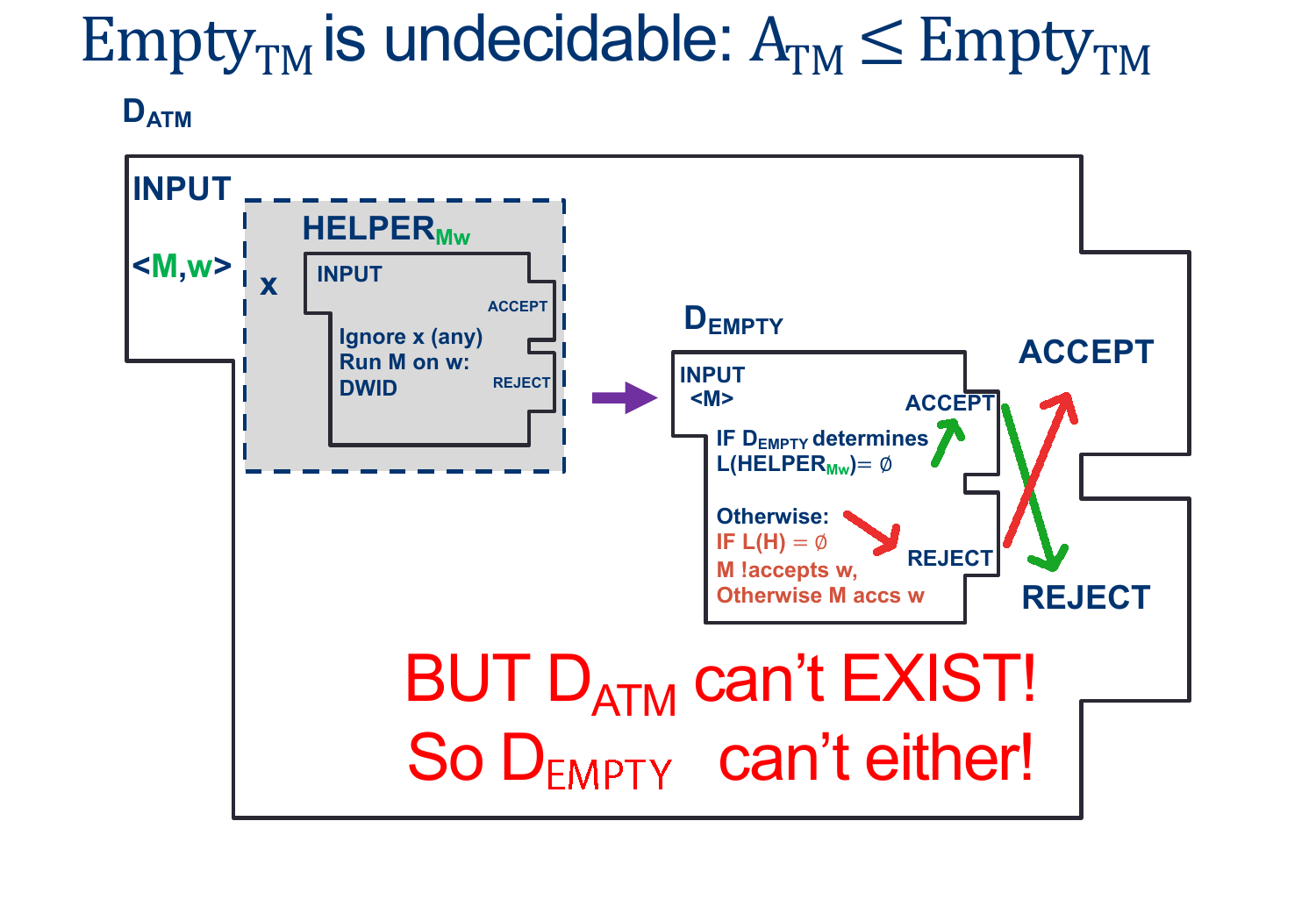
Assume EMPTY-TM is decidable, and so there exists some \(D_{EMPTY-TM}\) that decides, for any input \(< M >\), whether \(L (M) \) is empty.

We'll design the Machine \(D_{ATM} \) as follows:

\[ \begin{align*} &D_{ATM}:\\ & \text{ On input $ < M, w > $ }:\\ & \text{ Create (but don't run) $HELPER_{M,w}$ such that}\\ & \quad \text{ On input $ < X > $ }:\\ & \quad \quad \text{ Ignore $ < X > $ }\\ & \quad \quad \text{ Run $M$ on $w$ ADWID}\\ & \text{ Now Run $D_{EMPTY-TM}$ on $HELPER_{M,w}$}\\ & \text{ If $D_{EMPTY-TM}$ rejects, invert the result and our machine ACCEPTS}\\ & \text{ If $D_{HALT}$ accepts, , invert the result and our machine REJECTS}\\ \end{align*} \]

As we saw above, the ONLY way \(D_{EMPTY-TM}\) Rejects is if \(HELPER_{M,W}\) Accepts, which happens ONLY when \(M\) accepts \(w\).

This means we CAN make \(D_{ATM}\) as long as \(D_{EMPTY-TM}\) exists.

However, \(D_{ATM}\) doesn't exist...which means \(D_{EMPTY-TM}\) CANNOT EXIST EITHER.

















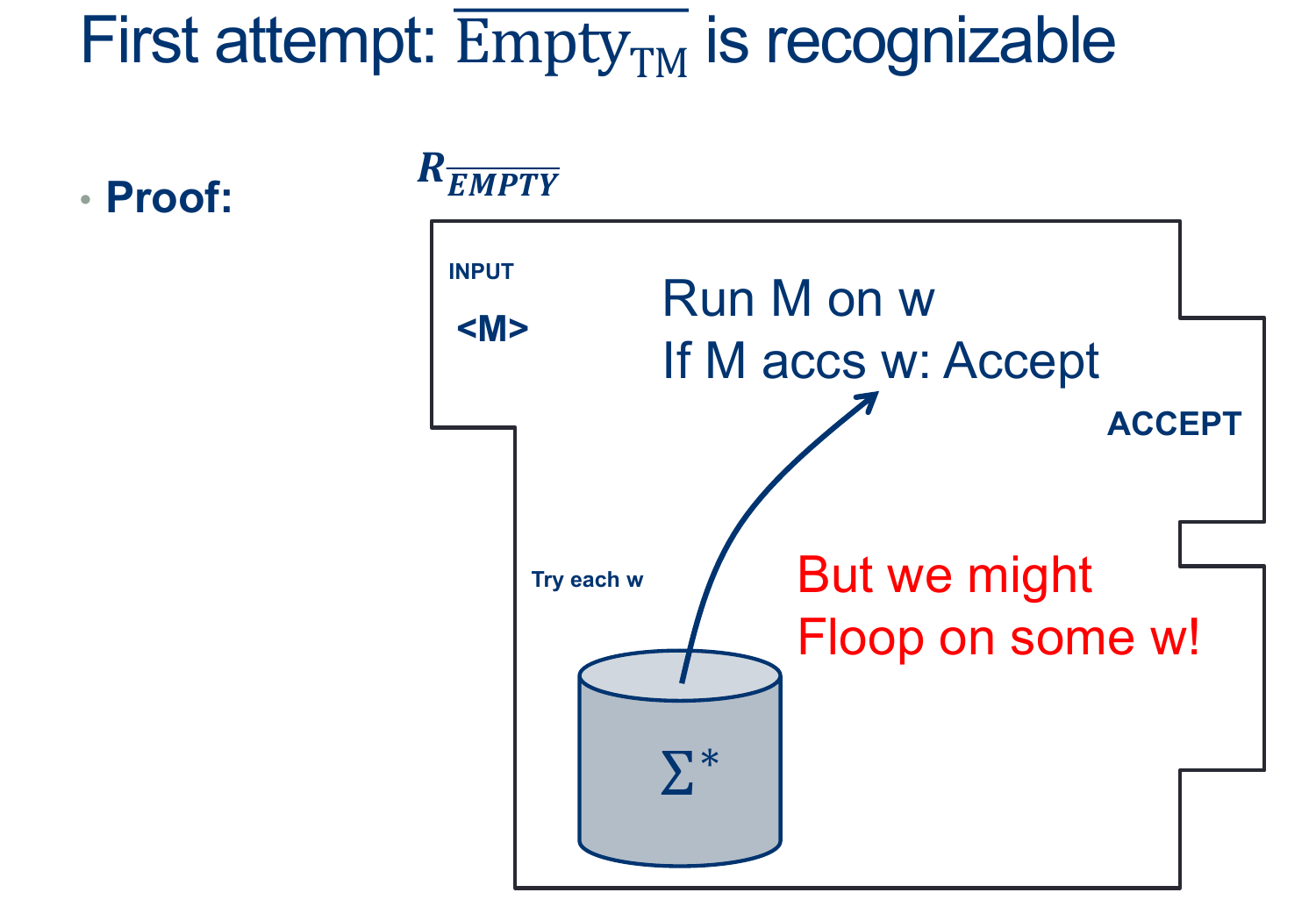
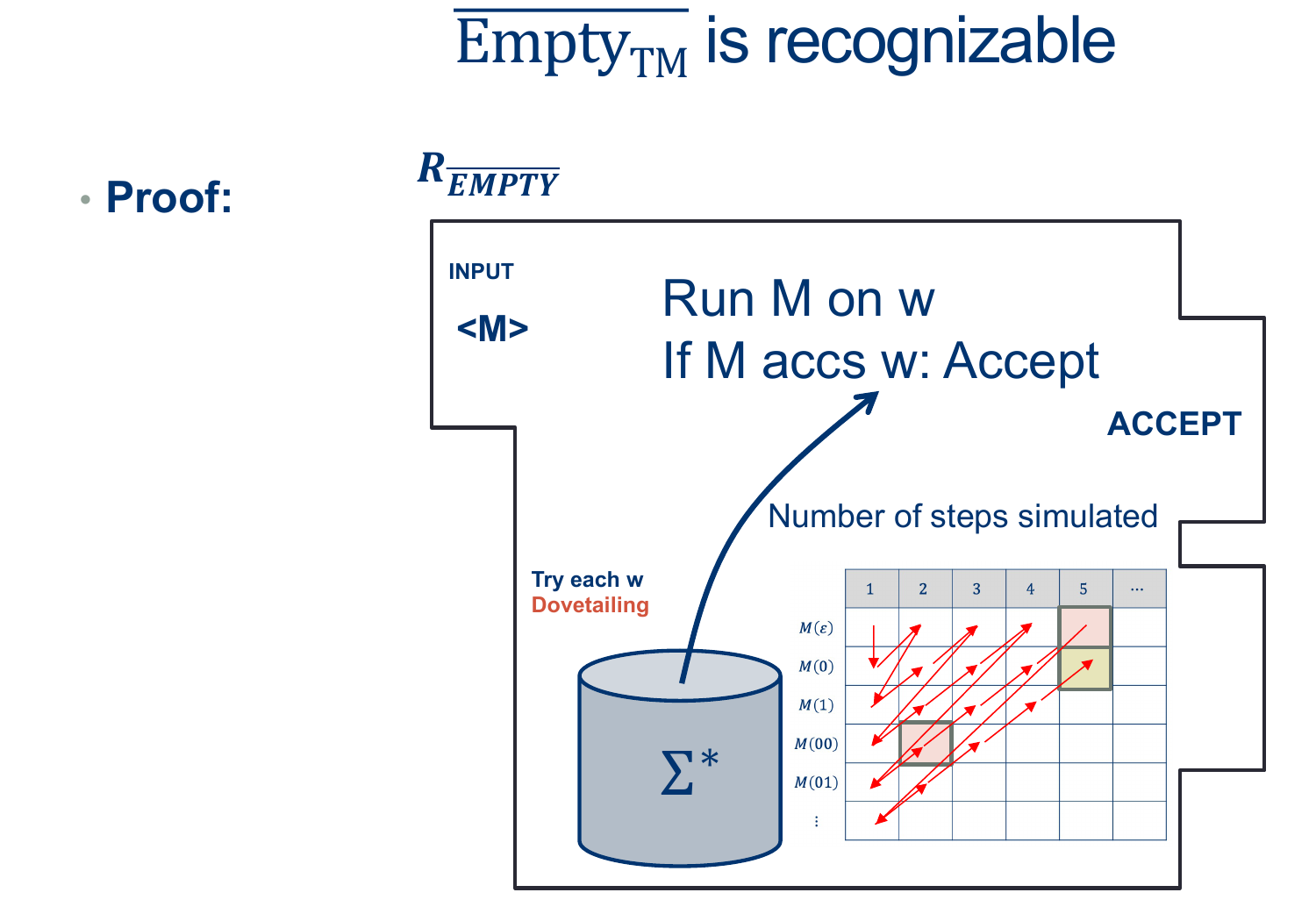This will lead us to a new way of looking at Recognizers: Enumeration.



Homework


[Due for everyone]
Get together to study Reductions!!
You need to be able to master reducing the examples we've seen so far.

[Optional]
TODO