SmithLogo

CSC 250

Theory of Computation

Smith Computer Science



Lecture Notes 14: Intro to Turing Machines


Outline

This class we'll discuss:



Building up to the big one...



Turing Machines









































































So, a transition would look like this:
\[ (r, w, m) \]
where each of the elements means:
  • r: what is Read from the "tape"
  • w: what is Written into the "tape"
  • m: the movement direction in the "tape"
Examples:
  • (0, \(\square\), L): IF we read a 0, we write a "blank" and move Left
  • (1, 1, R): IF we read a 1, we write a 1 and move Right
  • (0, 0, L): IF we read a 0, we write a 0 and move Left
















(Wait; then Click)

 Solution





Where would the reject state be?


































The magic Halting predictor machine H

Can we create a machine/routine (let's call it machine H) that can predict if a program will halt?

Let's watch the following video to see what could go wrong with such a machine H:
Halting Problem Video







Proof Sketch

The following is a (sketch of a) proof by contradiction:



1: Say there exists a function called halts


halts(f) returns true if the subroutine f halts and returns false otherwise.



2: Now consider the following subroutine g:







What is happening here?
(Wait; then Click)
  1. halts(g) must either return true or false.
  2. If halts(g) returns true, then g will call loop_forever and never halt, which is a contradiction.
  3. Therefore, the initial assumption that halts is a total computable function must be false.






Next class: Decidability



Information about the Midterm

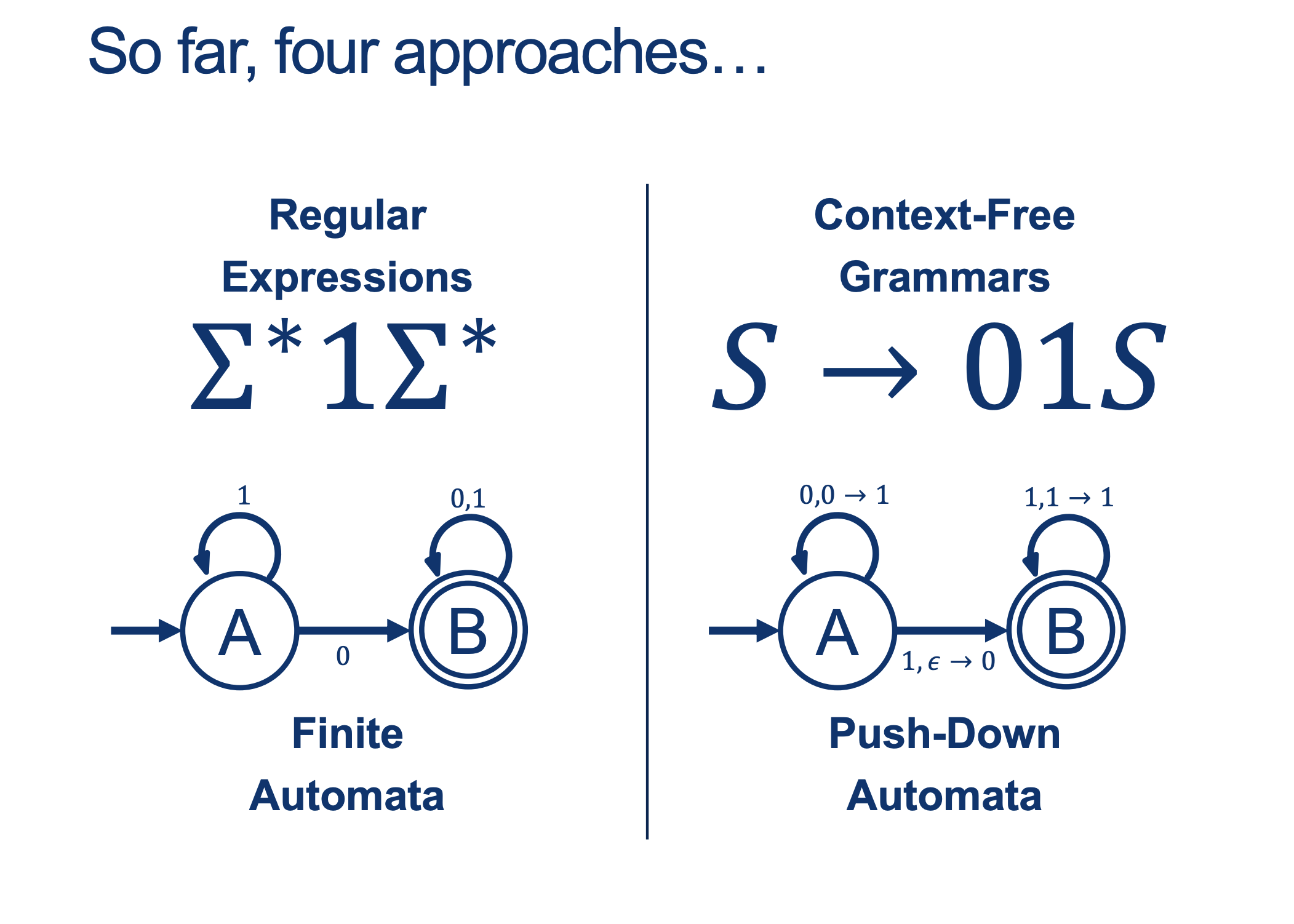
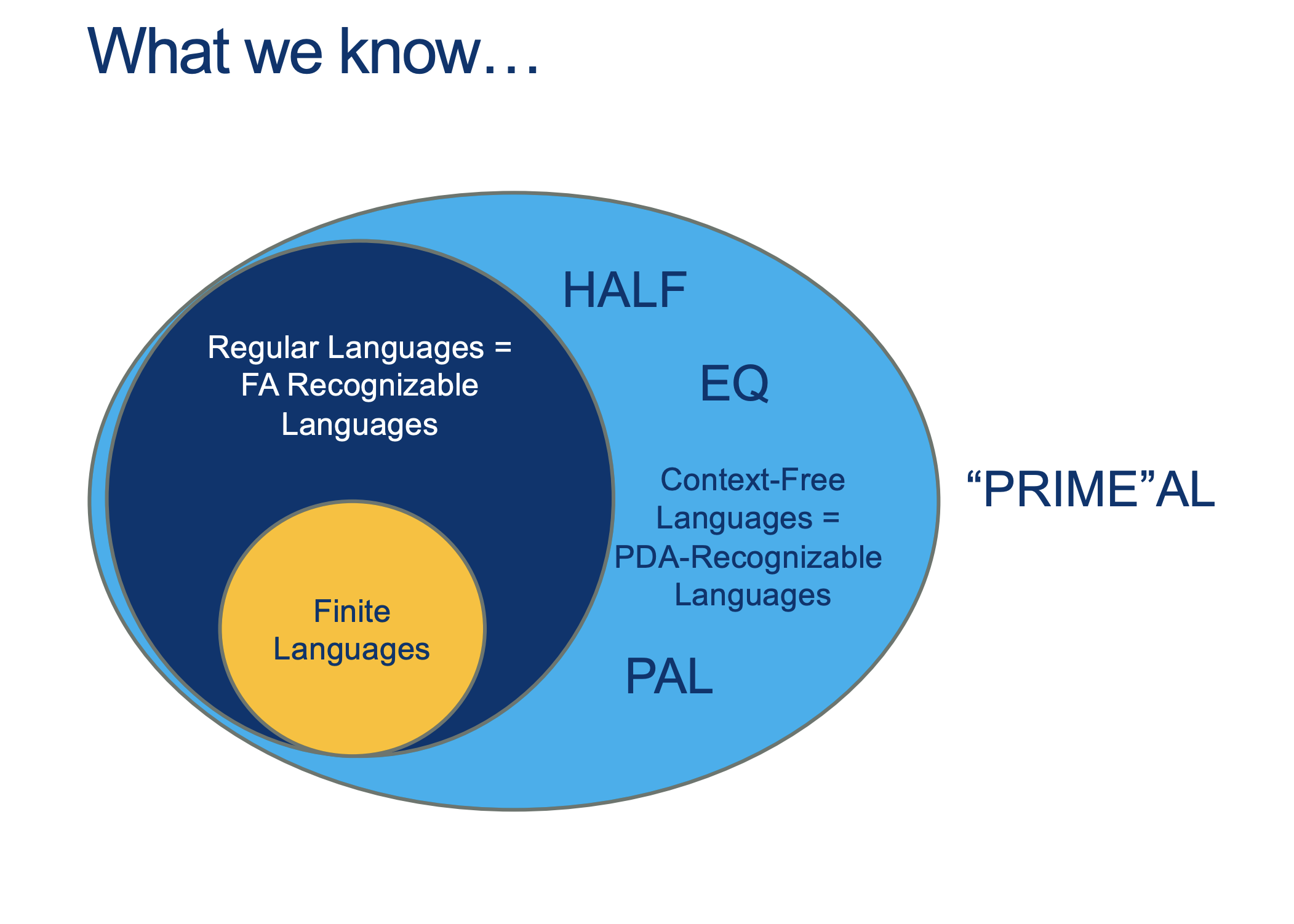
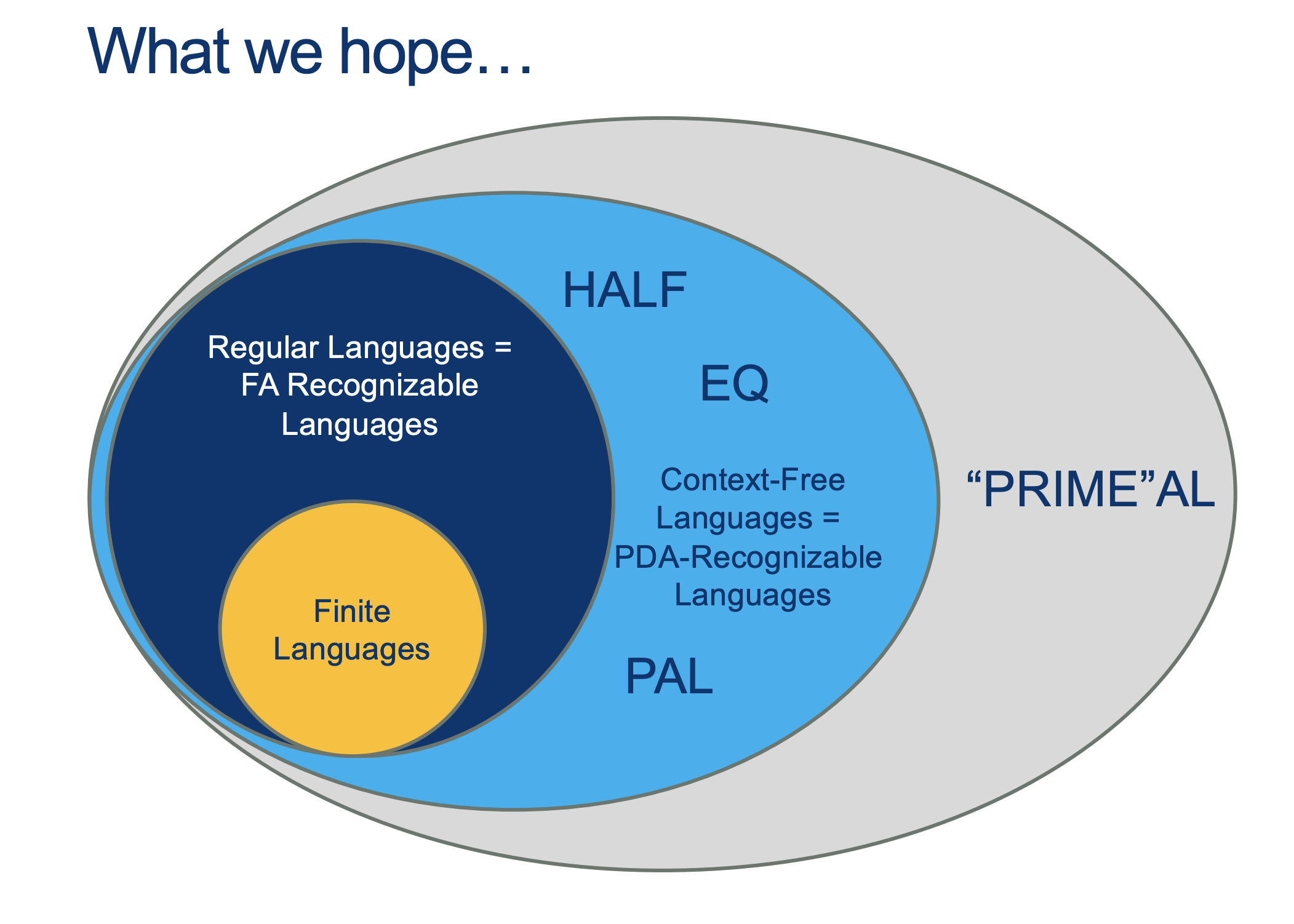
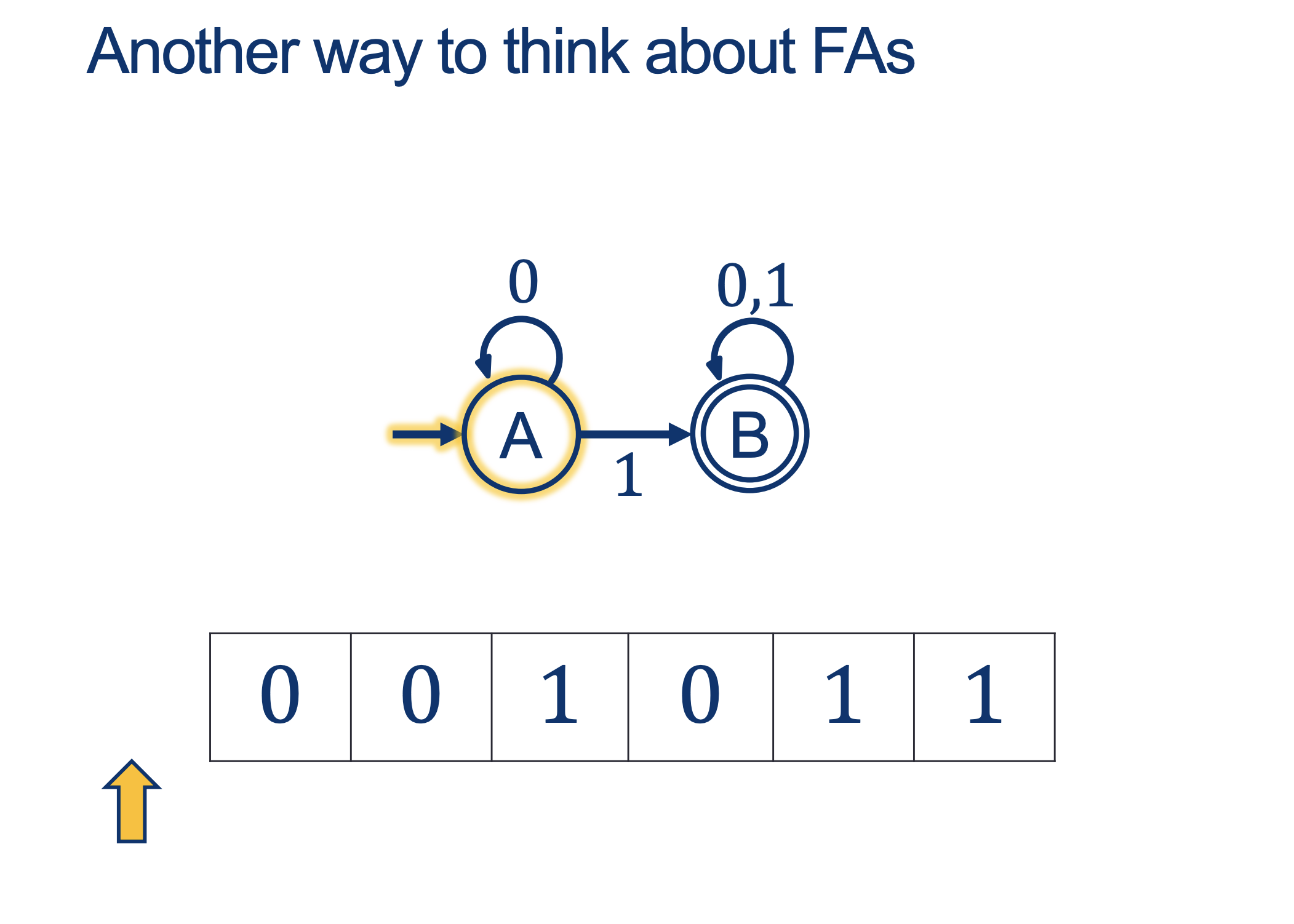
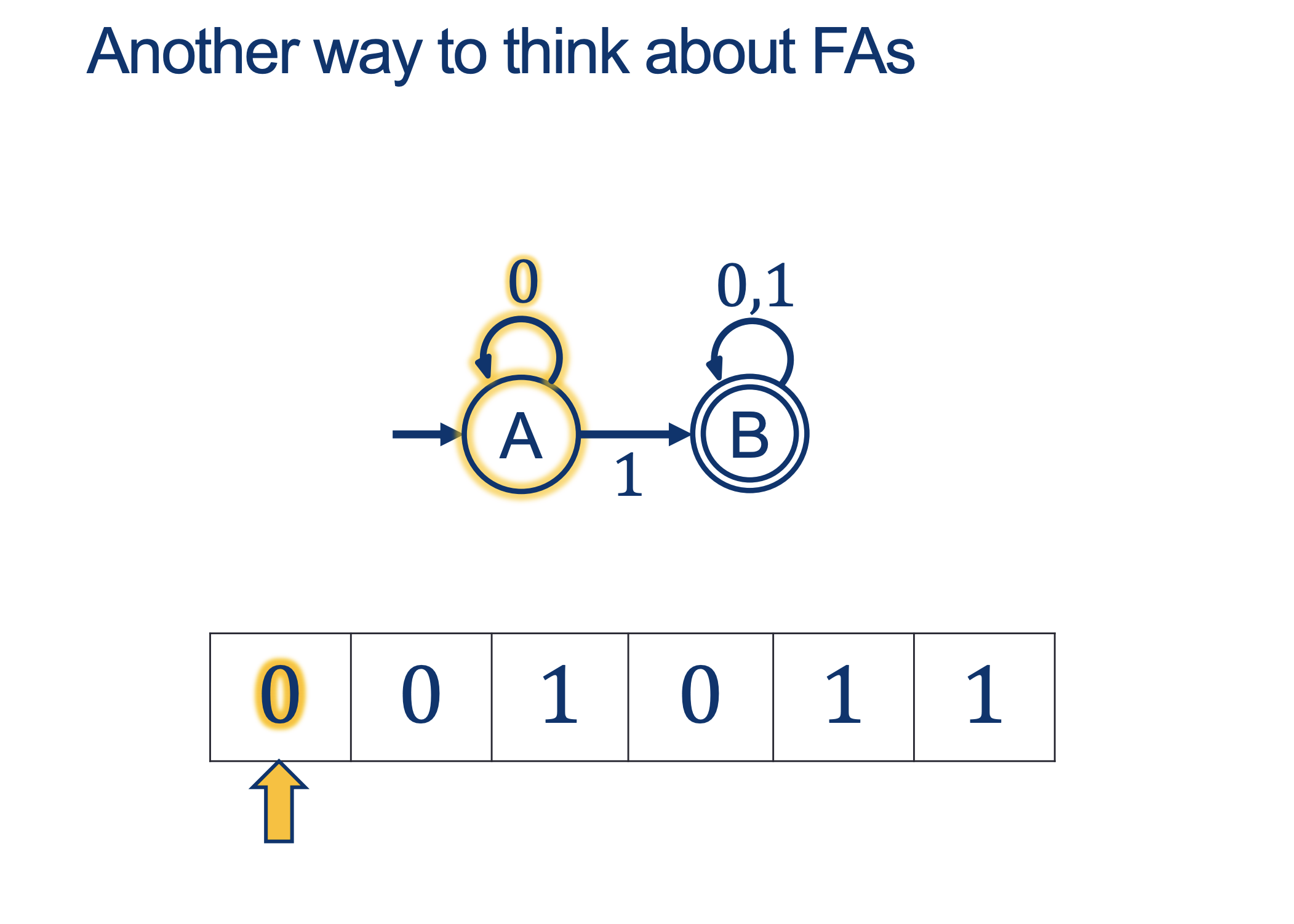
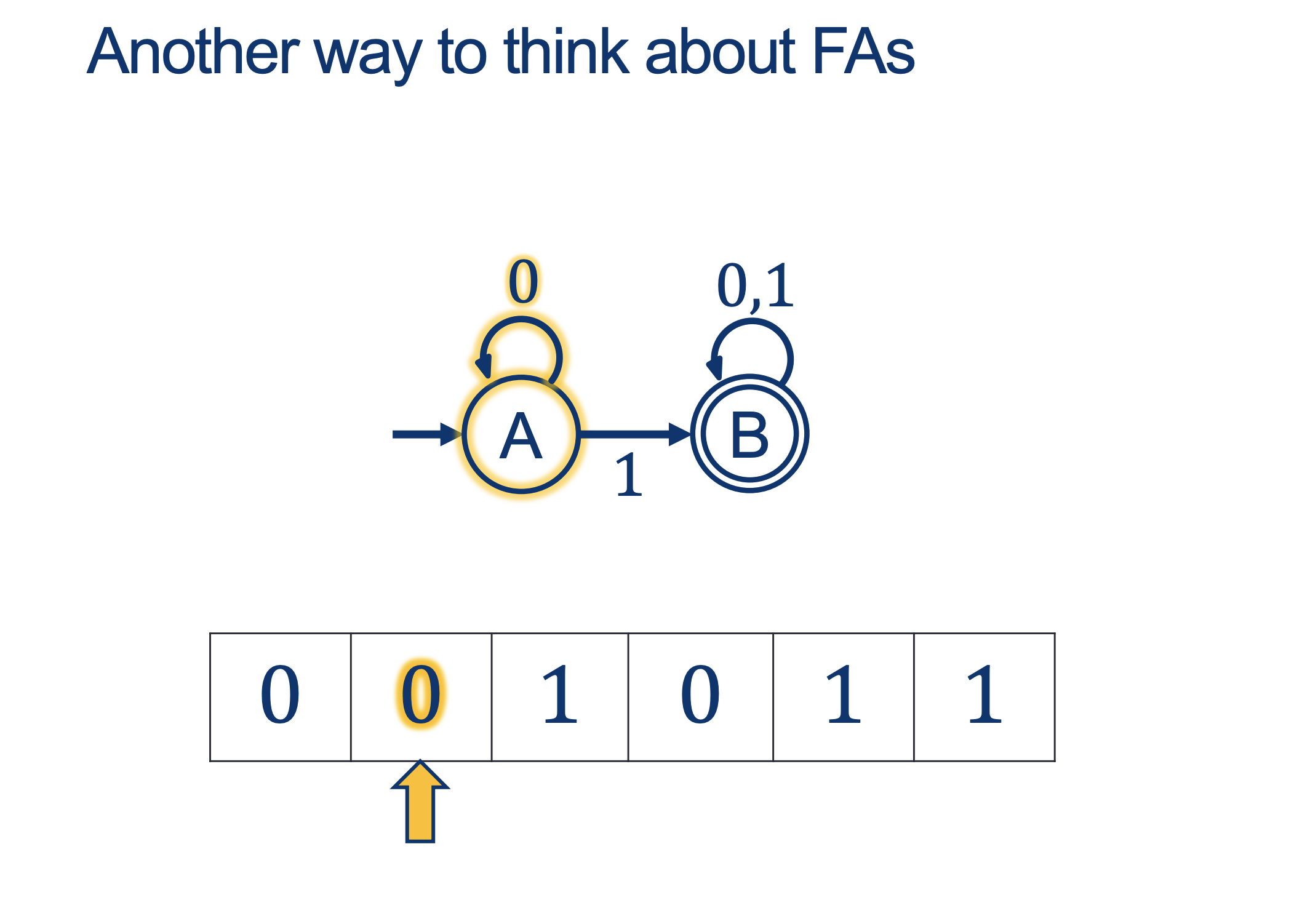
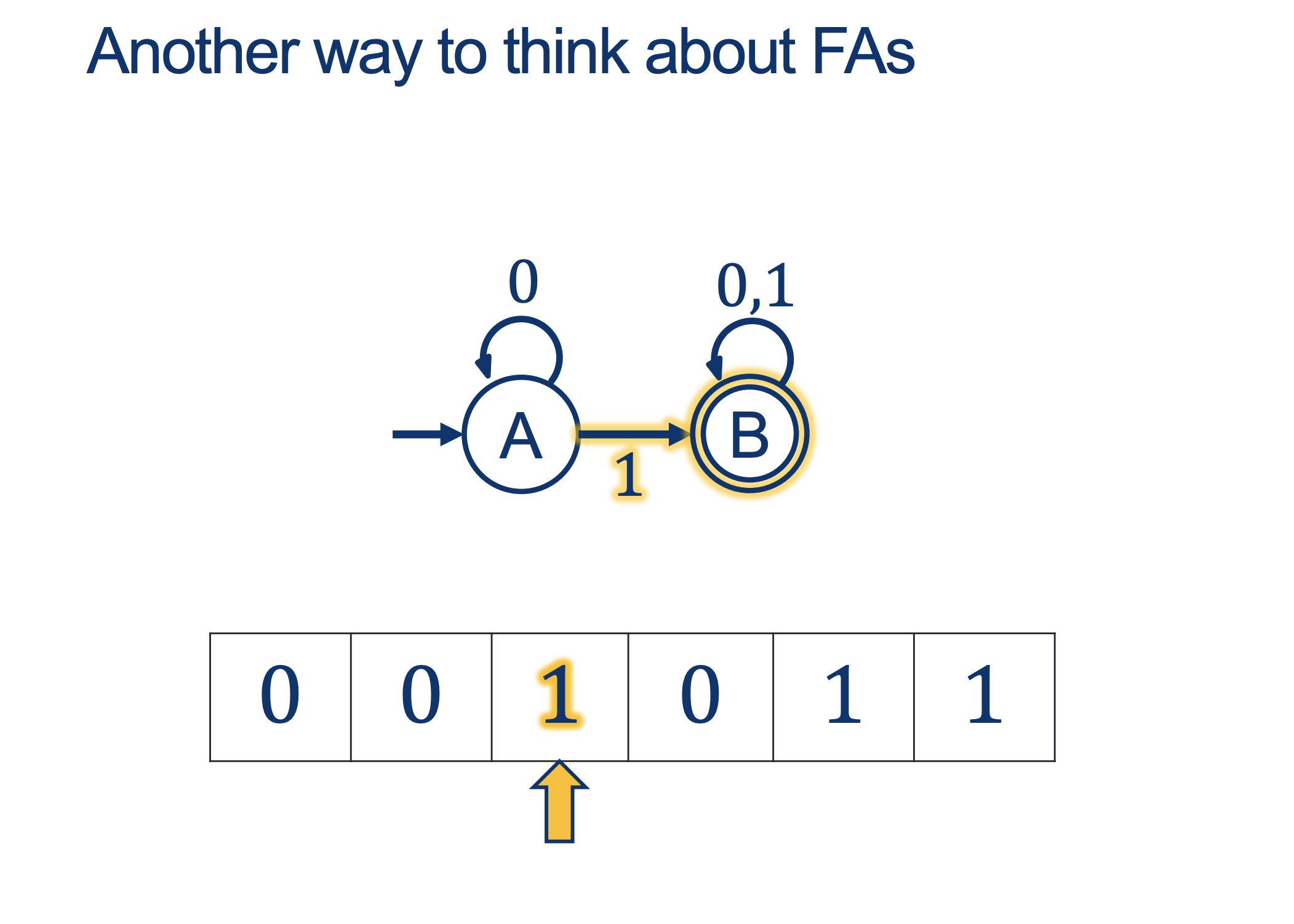
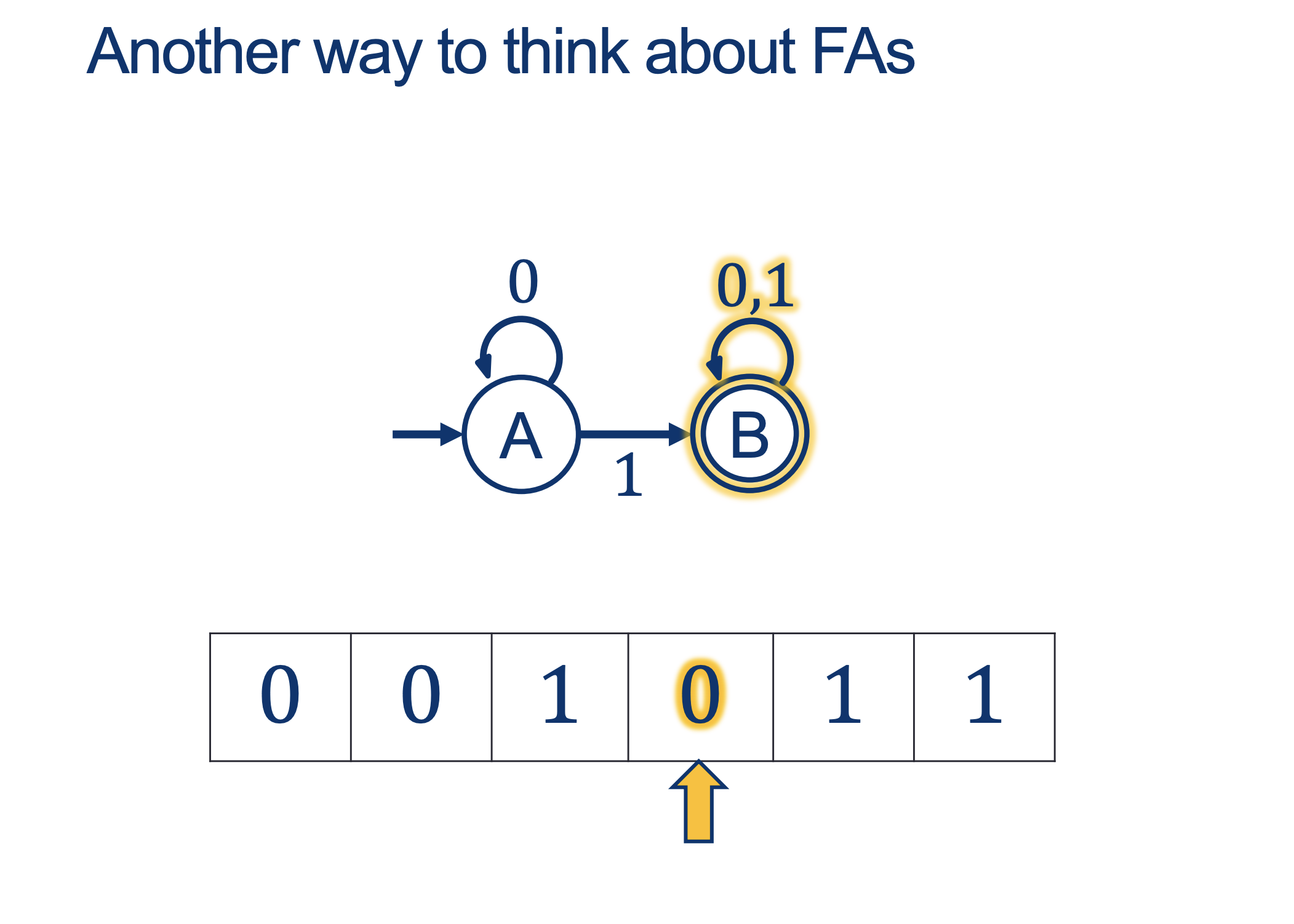
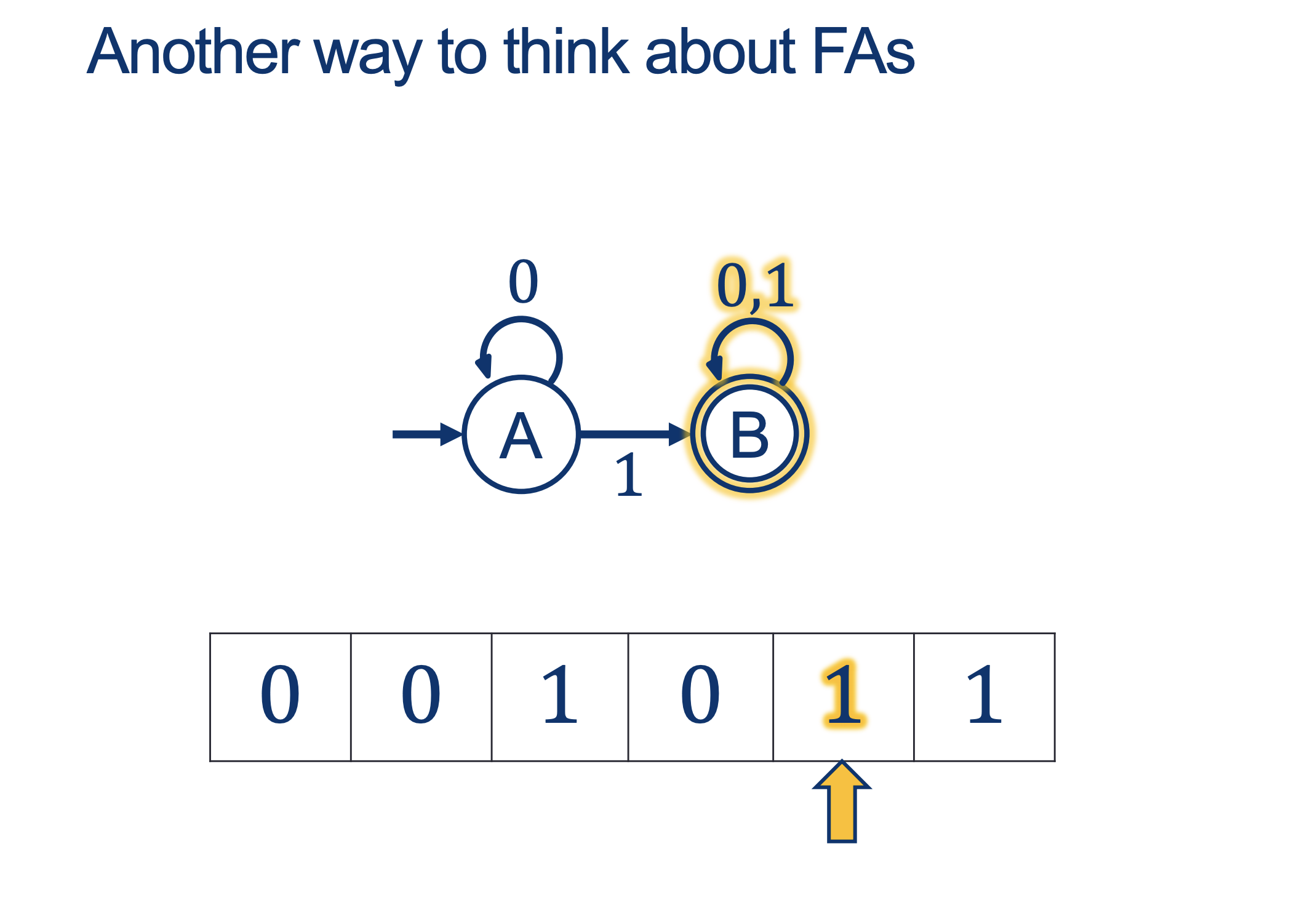
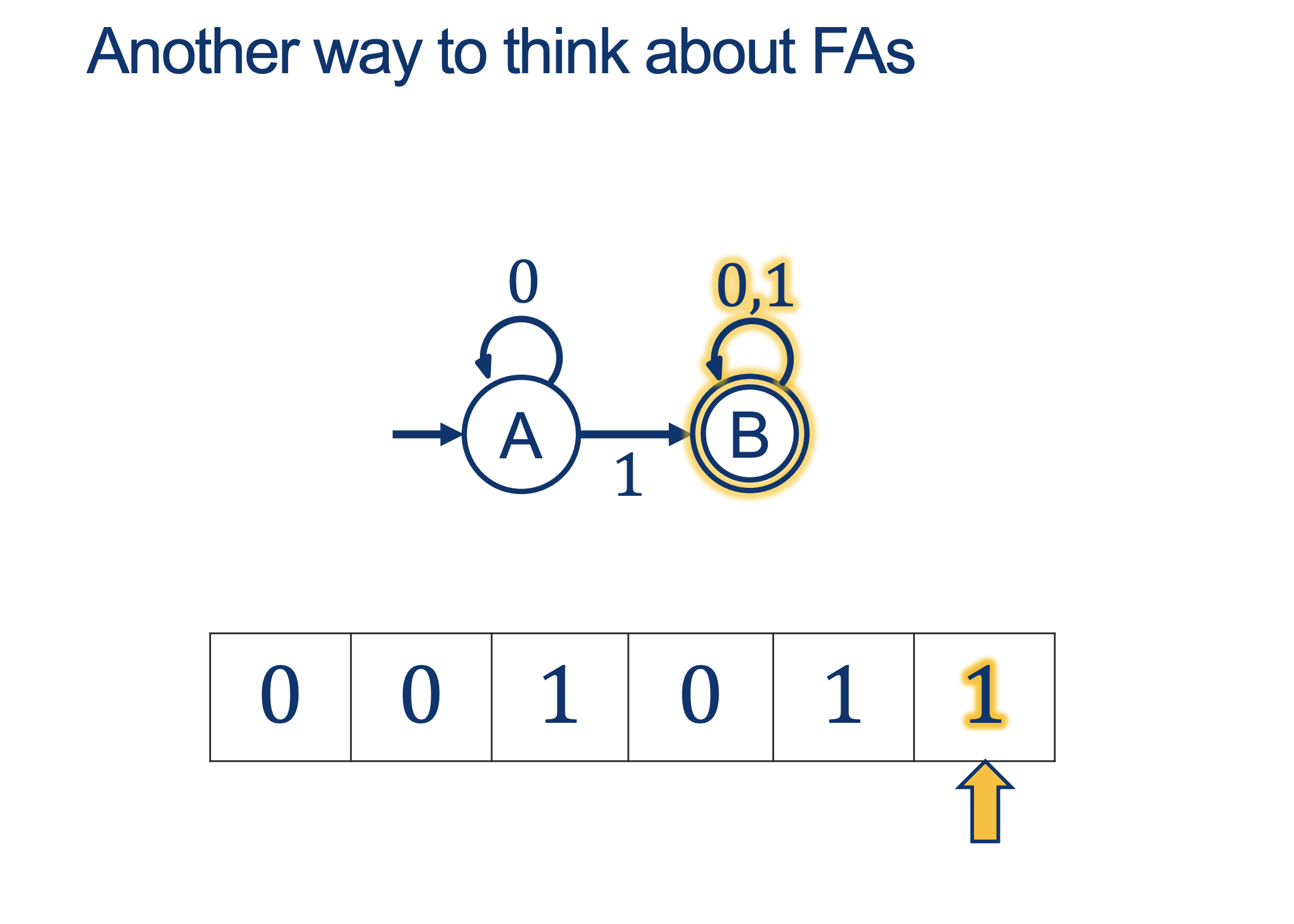
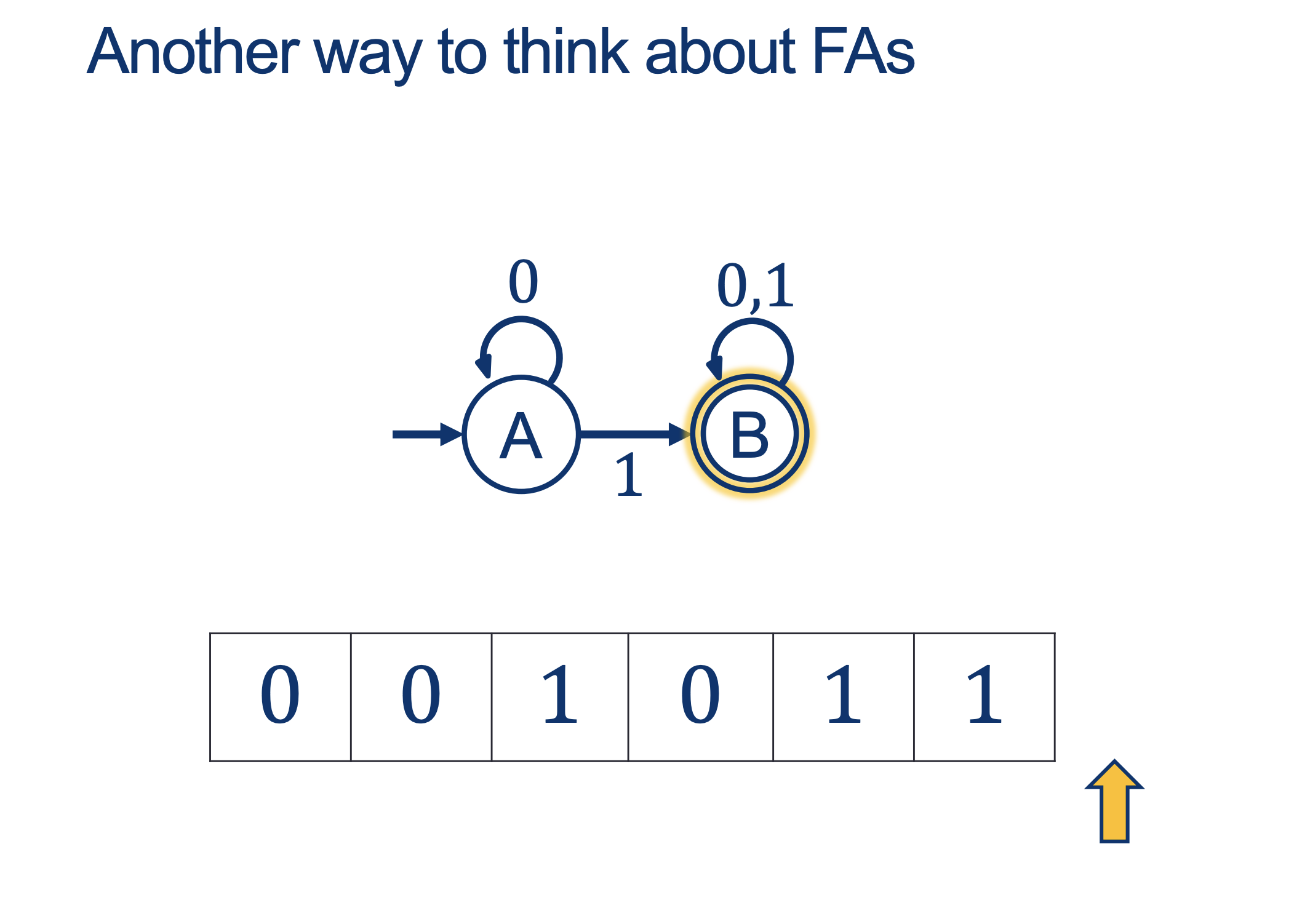
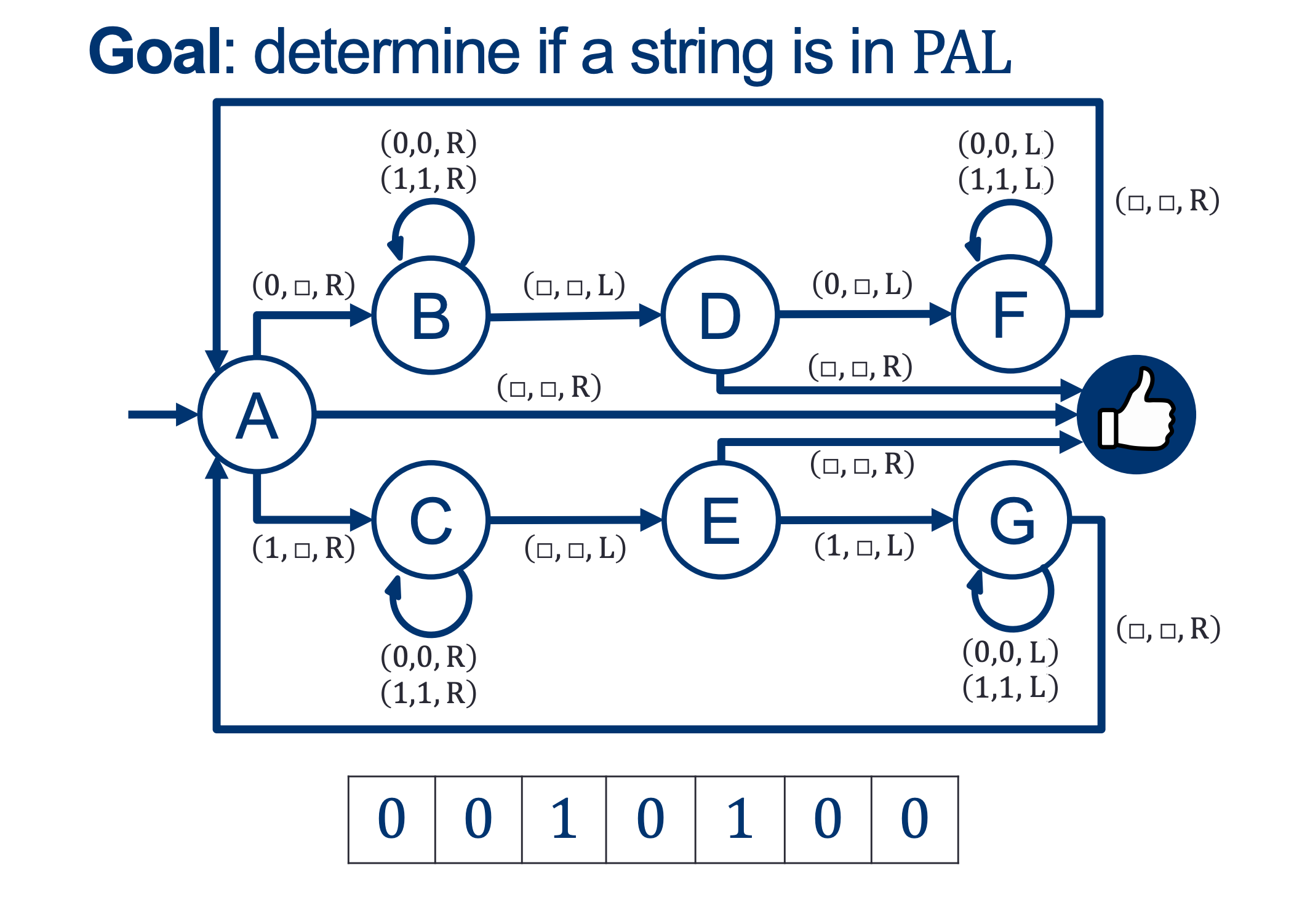
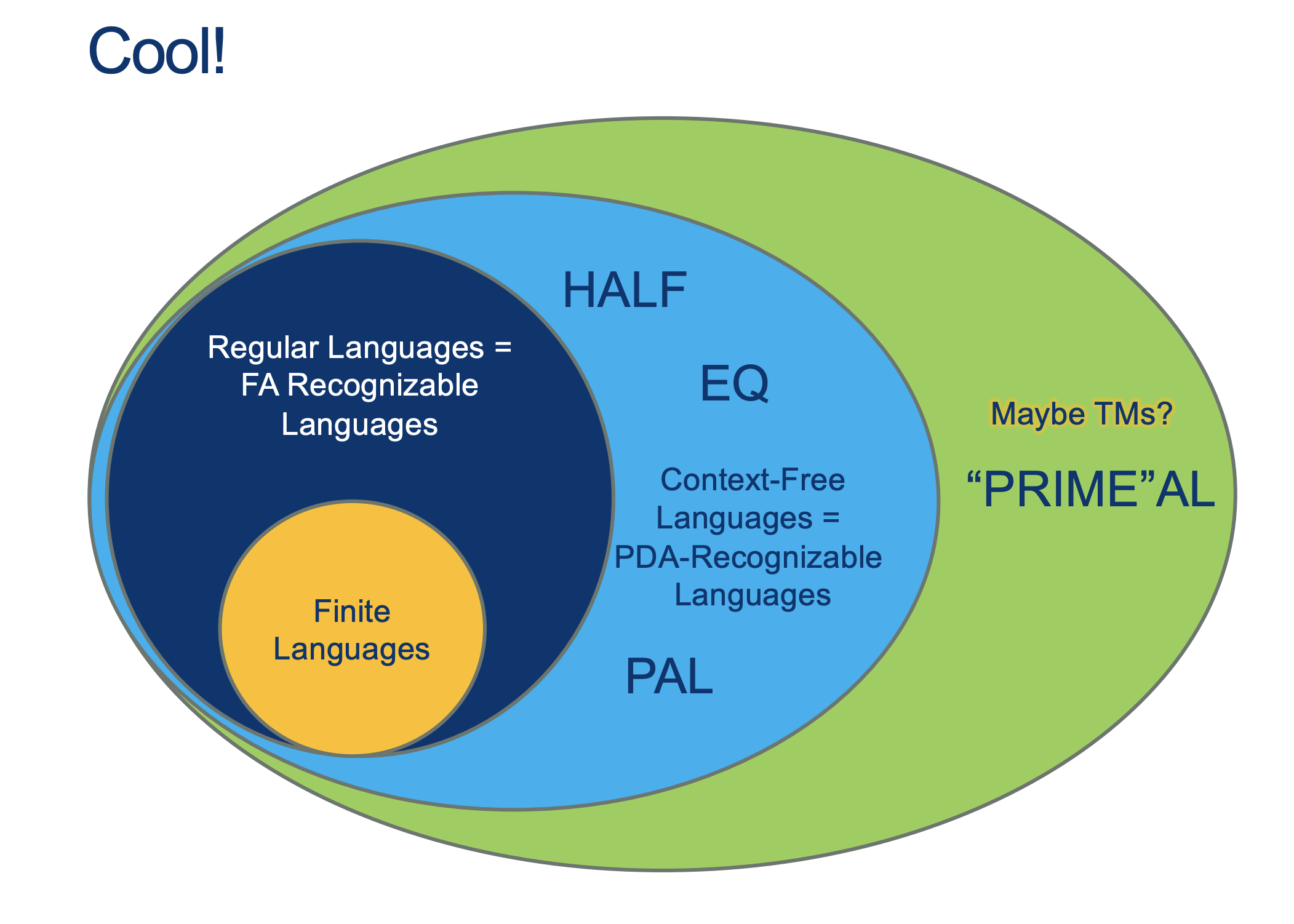
We will hold Self-Scheduled exams AFTER the spring break (the following weekend).

The projected dates are March-25th to March-27th.

We will do a review upon your return to help get you in tip-top form.

It will cover:

You have to be able to:



Homework


[Due for everyone]
TODO

[Optional]
TODO