Lecture Notes 02: Intro to Logic and Proofs
Outline
This class we'll discuss:
- Why logic?
- Crash course in logic
- What makes a good proof?
- Three kinds of proofs:
- Direct
- Contradiction
- Contrapositive
Bird's eye view
Remember: we will have to convert real-life problems to language (symbols, operators, delimiters, quantifiers,...) so we can talk about them, and hopefully solve them, in the abstract.
So... we must agree on some rules about symbol manipulation and drawing conclussions. That is why we'll discuss how to argue a point in such a way that it leaves no room for "comebacks"/"clapbacks"/"retaliation", etc ... in short: in such a way it does not leave the door open for a counter argument.
Logic and Logical Thinking
Activity 1 [2 minutes]: What is Logic and logical thinking?
One possible answer:
(Wait; then Click)
The process of obtaining a conclusion from a set of propositions taken to be true.
Two Examples
-
Easy one:
- Dogs are better than Cats (Proposition or Premise A)
- Cats are better than Parrots (Proposition or Premise B)
- Therefore: Dogs are better than Parrots (Proposition or Conclusion C)
Note that since we've determined that "All Dogs are better than Parrots"
we can now use this as another proposition.
-
A Difficult one:
- If Yak barks, I can't work
- If I can't work, students are assigned no homework
- If students have no homework, students are happy
- Students are happy
- Therefore: \( ??? \)
we'll analyze these and more examples using some structure.
Activity 2 [2 minutes]: if we just use English to analyze the material,
what could go wrong?
One possible answer:
(Wait; then Click)
Ambiguity!.
Example:
If a waiter asks: "Would you like a burger or a hotdog?"
You could answer: "Yes".
Where is the linguistic issue in this exchange?
Other issues: language artifacts, like contronyms (dust, clip, fast), or
homonyms ( "Buffalo buffalo buffalo Buffalo buffalo").
We need to use some structure to keep track of and operate with propositions that are unambiguous.
For this, we'll use some
agreed-upon terminology.
As an
alternative mode of visualizing the concepts, whenever possible,
we'll make use of
Venn Diagrams.
Terminology
- A proposition is a statement that has a truth value (either true or false).
Example:
- The Proposition: "All prime numbers are odd", has a truth value of false
- A proposition has internal structure:
It states that all or some members of a set have a property that makes them members of another set.
Example:
The subject ("grass") refers to the part of the proposition that is to be the focus of the statement.
The predicate("is green") indicates a property of the set of elements pointed to by the subject.
-
Quantifiers enable us to build propositions with degree:
Example:
- "All grass is green"
- "No grass is green"
- "Some grass is green"
Propositional Logic
The process by which we can combine propositions, in a logical computation, to obtain valid conclusions
OR
with which we can detect errors in the logical computation and refute a conclusion.
Activity 3 [2 minutes]: how do we combine propositions?
Logical Operators
In this section we'll discuss logical operators, which are rules that indicate the resulting effect on a proposition or a set of propositions when operated upon.
Negation
The negation operator, symbol: \( \neg \), AKA NOT, is a unary operator and it refers to the opposite truth value of a proposition.
We can show the effect of this operator using a table:
| p |
¬p |
| True |
False |
| False |
True |
another view:
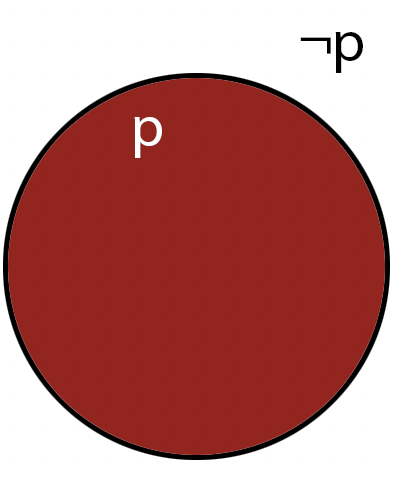
Example: I am not Swedish.
Note: other symbols you might see are: \( \neg p \text{, } \sim{p} \text{, } \bar p \text{, } !p \).
Conjunction
The conjunction operator, symbol: \( \wedge \), AKA AND, is a binary operator; it is true if and only if both of its operands are true.
We can show the effect of this operator using a table:
| p |
q |
p∧q |
| False |
False |
False |
| False |
True |
False |
| True |
False |
False |
| True |
True |
True |
another view:
| p |
q |
p∧q |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
 Note that we're labeling on the outside for clarity, but the label refers to the interior of each circle
Note that we're labeling on the outside for clarity, but the label refers to the interior of each circle
Example: I am walking and chewing gum.
Note: other symbols you might see are: \( p \wedge q \text{, } p\cdot q \text{, } p\&q \).
Disjunction
The disjunction operator, symbol: \( \lor \), AKA OR is a binary operator; it is true if any of its operands is true.
We can show the effect of this operator using a table:
| p |
q |
p∨q |
| False |
False |
False |
| False |
True |
True |
| True |
False |
True |
| True |
True |
True |
another view:
| p |
q |
p∨q |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
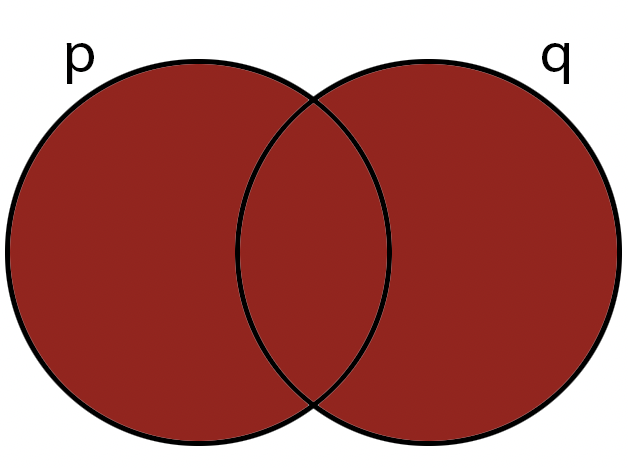
Example: I want a burger or a hotdog.
Note: other symbols you might see are: \( p\lor q \text{, } p+ q \text{, } p\mid q \).
Exclusive Disjunction
The exclusive disjunction operator, symbol: \( \oplus\), AKA XOR is a binary operator; it is true if its operands are different.
We can show the effect of this operator using a table:
| p |
q |
p\( \oplus \)q |
| False |
False |
False |
| False |
True |
True |
| True |
False |
True |
| True |
True |
False |
another view:
| p |
q |
p\( \oplus \)q |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
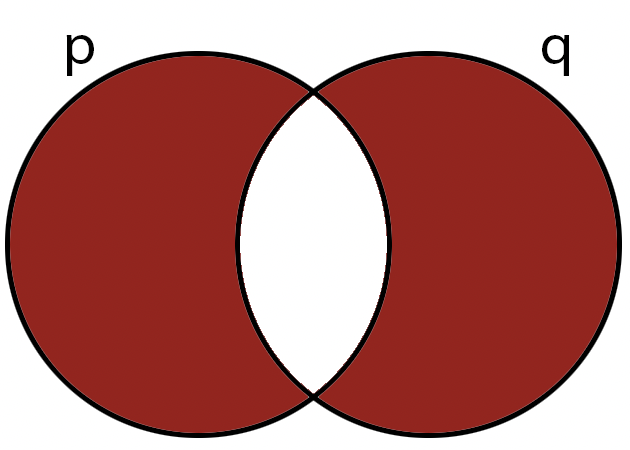
Example: No equivalent in the english language... or is there? (** suspenseful music **)
Note: other symbols you might see are: \( p\nleftrightarrow q \text{, } p\veebar q \text{, } p\not\equiv q \).
Compound Propositions
We can combine these building blocks to make arbitrarily complicated propositions:
\[ (p \wedge ¬q) \lor (\neg p \wedge q) \]
Activity 4 [2 minutes]: What is this saying?
More operators: Implication
Implication, symbol \(\rightarrow\), AKA IMPLIES, is a binary operator that states that:
IF p is true, then q must also be true
We can show the effect of this operator using a table:
| p |
q |
p\( \rightarrow \)q |
| False |
False |
True |
| False |
True |
True |
| True |
False |
False |
| True |
True |
True |
Think of the whole statement as a promise;
You only "tag" it as FALSE when you break the promise.
Rows 3 and 4 are the "normal" ones:
-
In Row 3, The promise "IF p is True, then q is also True" has been broken! (because q is NOT True)... so the statement is False (the promise is broken)
-
In Row 4, the "IF p is True, then q is also True" has been kept! so the whole statement is True!
But what is happening in rows 1 and 2?
Rows 1 and 2 are
True because they "technically" are not breaking the promise. We call the Truth value of these statements "Vacuous Truths"
-
In Row 1, The promise "IF p is True, then q is also True" is not being employed (because p is NOT True), regardless of the value of q... so the statement is True (the promise is not broken)
-
In Row 2, The promise "IF p is True, then q is also True" is not being employed either (because p is NOT True), regardless of the value of q... so the statement is True (the promise is not broken)
Examples:
- "All my children are goats" is a vacuous truth, when spoken by someone without children
-
For the implication "For any integer \(x\), if \(x > 5 \rightarrow x > 3 \)",
some of its implications are vacuously true, like when \(x\) is 2, which implies the vacuous truth that
if \(2 > 5 \rightarrow 2 > 3 \)
-
Another example would be:
"All living people in the world are resistant to moonlight"
This can be written as:
if \( \text{P: living person} \quad \text{and M: resistant to moonlight} \), then the statement is:
\(P \rightarrow M\)
The combination when \( \neg P \text{ (not P, or P:False) and } \neg M \text{ (not M, or M:False) } \)
Would be True: \(\neg P \rightarrow \neg M\)
So the sentence:
All the vampires in the world are susceptible to moonlight"
Is (vacuously) True (I hope).

The left of the \(\rightarrow\) operator in an implication is called the
antecedent, and the sentence to the right is called the
consequent.
The best way to remember the way implication works is with this statement:
The truth value of an implication is false if and only if its antecedent is true and its consequent is false; otherwise, the truth value is true.
Activity 5 [2 minutes]: Can you draw the Venn Diagram for this one?
(Wait; then Click)
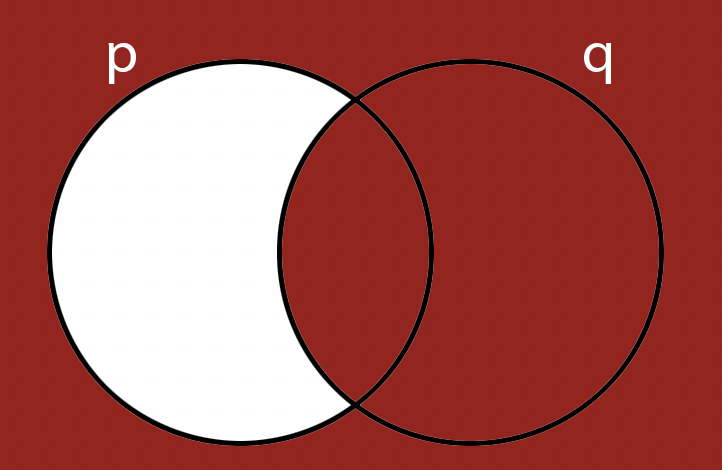
More operators: If and only if
If and only if, symbol \(\Leftrightarrow\), AKA IFF, is a binary operator that states that:
IF p is true, then q must also true, and IF q is true, then p must also true!
We can show the effect of this operator using a table:
| p |
q |
p\( \rightarrow \)q |
p\( \leftarrow \)q |
p\( \Leftrightarrow \)q |
| False |
False |
True |
True |
True |
| False |
True |
True |
False |
False |
| True |
False |
False |
True |
False |
| True |
True |
True |
True |
True |
Activity 6 [2 minutes]: Can you draw the Venn Diagram for this one?
If you look at the p, q, and p\( \Leftrightarrow \)q columns, you might see something that looks familiar
One possible answer:
(Wait; then Click)
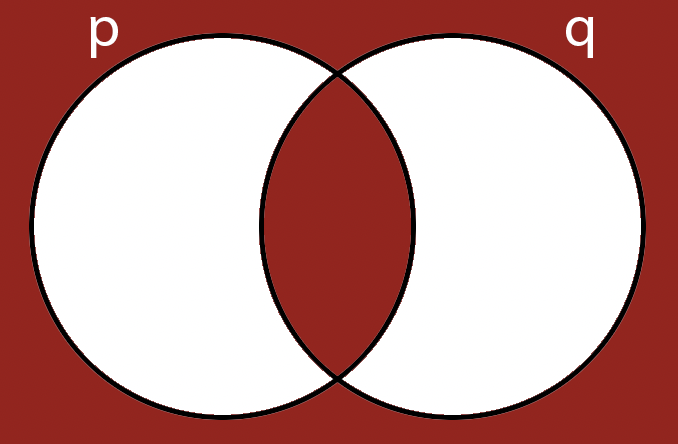
Inference
Inference is the process of obtaining logical consequences from premises.
Let's use an example:
Activity 7 [2 minutes]: What can you infer if you do not hear a honk?
You can assume that
we have a driver behind us;
the driver saw the sign;
they have a working horn
people in this town take bumper stickers seriously
Symbolic manipulation
For some problems, holding the information in our head and making sense of it is quite hard.
Luckily, we have been building a symbolic language that can take the place of "thoughts that make sense so far" so that
we can continue doing our logical computation.
Precedence
We have accumulated some symbols:
- parentheses
- \(\neg\)
- \( \wedge \)
- \(\lor\)
- \(\oplus\)
- \(\rightarrow\)
- \(\Leftrightarrow\)
when several of the same operator are in a row (i.e. \(a ∧ b ∧ c\)), evaluate from left to right.
(There are a couple of cases where this is not true, but we won't look at those here)
Curious Constructions: Tautology
Activity 8 [4 minutes]: What can you tell about the following proposition?
\[ (p \lor q) \wedge (\neg q) \rightarrow p \]
Answer below
| p |
q |
p ∨ q |
¬q |
(p ∨ q) ∧ (¬q) |
(p ∨ q) ∧ (¬q) →p |
| 0 |
0 |
0 |
1 |
0 |
1 |
| 0 |
1 |
1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
0 |
1 |
1 |
A Tautology is an assertion that is always true.
In its most basic form, it is:
\[ q \lor \neg q \]
Curious Constructions: Contradiction
Activity 9 [1 minute]: What can you tell about the following proposition?
\[ q \wedge \neg q \]
answer:
(Wait; then Click)
This proposition is always false!
A Convincing Argument
In spoken English we talk of "making a point".
We usually "grant" said point when the person has made a convincing argument or revealed an unforeseen truth.
As we mentioned before, using English leaves you exposed to ambiguity, contradictions, or language artifacts.
In propositional logic, we can create a convincing argument using propositional logic by chaining together a series of boolean statements until we get to the desired conclusion.
A Logic puzzle
Aleks, Benita, Chas, and Dora are quadruplets, and they’ve all been invited to a birthday party.
Unfortunately the quadruplets don’t get along very well:
- If Aleks goes to the party, then Benita will not go.
- If Chas goes to the party, then Aleks will not go.
- If Dora goes to the party, then Chas will not go.
Activity 10 [4 minutes, if we have time]: What is the largest possible number that will go to the party?
Proofs
We will see a very high-level intro to three types of proofs:
- direct proofs (deduction)
- proof by contradiction
- proof by contrapositive
Direct proof deduction
To quote Wikipedia: "Deductive reasoning goes in the same direction as that of the conditionals, and links premises with conclusions. If all premises are true, the terms are clear, and the rules of deductive logic are followed, then the conclusion reached is necessarily true."
Example:
- Yak is the best dog
- half of all dogs are better than all cats
- Therefore: Yak is better than all cats
Proof by Contradiction
Start by assuming (taking as a true proposition) the opposite of what you wish to prove.
Follow the normal rules of propositional logic and if:
- You arrive at a valid conclusion: you were wrong
- You arrive at a contradiction: then the opposite of your initial assumption is true (what you wanted to prove)
Example:
Let's say we want to prove that: "there is no smallest rational number greater than 0"
Using proof by contradiction, we say:
- "there is a smallest rational number r greater than 0"
- however, we can make a new number s = r/2 that is >0 since r > 0
- Since s < r, and s is a rational number, then r was not the smallest
- Therefore: "there is no smallest rational number r greater than 0"
Proof by Contrapositive
If we take an implication proposition as true, there is another proposition we can extract from it by performing some manipulations:
To obtain the contrapositive of a proposition, we:
- negate both terms
- reverse the direction of inference
So if we have have the proposition \( p \rightarrow q \), then, the steps are:
- negate both terms: \( \neg p \rightarrow \neg q \) --->this is not correct...yet!
- reverse the direction of inference: \( \neg q \rightarrow \neg p \) --->this is the new proposition!
So, both \( p \rightarrow q \) and \( \neg q \rightarrow \neg p \) are true.
Example:
Let's say we accept that: "For any integer k, if 3k + 1 is even, then k is odd."
We could represent this symbolically:
- \(p\) is "3k + 1 is even"
- \(q\) is "k is odd"
- Then the phrase is: \(\forall k \in \mathbb{Z}, \text{ } p \rightarrow q \)
- Then the contrapositive of the phrase is: \(\forall k \in \mathbb{Z}, \text{ } \neg q \rightarrow \neg p \)
- Which translates to: "For any integer k, if k is not odd, then 3k + 1 is not even"
- OR more clearly: "For any integer k, if k is even, 3k + 1 is odd."
An example of a full proof by contrapositive would be:
Proof: We will prove the contrapositive of this claim,
i.e. that
for any integer k, if k is even, 3k + 1 is odd.
Suppose that k is an integer and k is even. Then, k = 2m for some integer m.
Then 3k + 1 = 3(2m) + 1 = 2(3m) + 1.
Since m is an integer, so is 3m. If we say n = 3m, Then 2(3m) + 1 = 2n + 1, which is an odd number.
This means 3k + 1 = 2(3m)+1 = 2n + 1 = an odd number, which is what we needed to show.
Example from the University of Illinois Urbana-Champaign, CS173
Activity 11 [4 minutes, if we have time]:
Prove the following statement: "Theorem: For any \(n \in \mathbb{Z}\), if \(n^2\) is even, then \(n\) is even."
Logical Errors
Activity 12 [4 minutes, if we have time]:
What is wrong with this statement:
If the weather is stormy, we can’t go swimming.
If we can’t go swimming, we won’t go to the beach.
We aren’t at the beach.
Therefore, the weather must be stormy.
Converse
The converse of an implication is is the result of inverting the direction of the implication, so if:
\( p \rightarrow q \)
The converse would be:
\( q \rightarrow p \)
The error would be in believing that just because an implication is true, its converse is too.
Example:
"Petting dogs makes me happy.
"I am happy, therefore I am petting a dog"
OR (Jordan's example!) "Being happy makes me pet dogs."
Inverse
The inverse of an implication is is the result of inverting (negating) its propositions while maintaining the direction of the implication, so if:
\( p \rightarrow q \)
The inverse would be:
\( \neg p \rightarrow \neg q \)
The error would be in believing that just because an implication is true, its inverse is too.
Example:
"Petting dogs makes me happy.
"I am not petting a dog, therefore I must not be happy"
Activity 12 [4 minutes, if we have time]:
Think about the following "puzzle":
A prosecutor in Logic Court (which is totally a thing) says to the defendant:
"If you committed the crime, then you must have had an accomplice" (this is known).
The defendant hotly denies that the implication is true.
Therefore, the jury (being apt logicians) convicts the defendant.
Explain what happened in this story.
Homework
[Due for everyone]: Go over any exercises we did not do in class (participation opportunity next class!)
Bring me questions and be ready to work in groups.
Before next Week's Thursday 09/15 at midnight EST
Note: (we'll normally try to do Assign: Wednesday; Due: Next Tuesday)
[Due for everyone] Problem Set 1
-
Problem Sets can be worked in teams of 3 students. (1 team of 4 MAX, with previous approval)
If you wish to be on a team, fill out this form to indicate one of two things:
- The names of the member of the team (2 or 3 teammates in addition to yourself)
- Indicate that you are OK being assignmed to a random team of 3 or 4 people
- A single person in the team submits a write-up (a pdf) to Moodle
- 2 pieces of information required for all submissions:
-
The names of all collaborating students be listed at the top of the submission.
-
A “References” section, with in-line citations to any resources you used.
If you did not use any resources, please state:
“I did not use any external resources in completing this assignment.”
Submitting Assignments in Latex using Overleaf
Overleaf is an online LaTeX editor.
What is LaTeX? you ask.
From https://www.latex-project.org/:
"LaTeX is a high-quality typesetting system; it includes features designed for the production of technical and scientific documentation. LaTeX is the de facto standard for the communication and publication of scientific documents."
How to Learn LaTeX?
I will provide templates for every Assignment where you only need to fill-in what your answer is. Whether it is text-only, text with mathematical symbols, equations, or even diagrams, there is a way to do it in overleaf.
Follow this
Oveleaf guide to learn LTeX in 30 minutes.
Overleaf has a set of quicklinks on the right side that have most (if not all) of what you'll need. Some of the most important things are the
symbols!.
Later on, we'll use the
FSM designer to make nice digrams like the ones shown below.
How to get started with A1?
I gave you a template in Moodle. The template is a Zip of a tex file, which holds the latex source code for A1. What you do is 1) download the zip, and 2) without unzipping, upload it to Overleaf (additional help/tutorials will be linked in mModle).
Overleaf lets you add a little bit of metadata info to a document to make it look better:











