SmithLogo

CSC 111

Introduction to Computer Science Through Programming

Smith Computer Science



Lecture Notes 09: Intro to Loops




Repetition is Necessary

Sometimes, we need to do work over and over again.

We've talked about ways to do this work in clever ways, for example: by using function calls

Example 1: Drawing a pyramid of stars 

 1  
 2  
 3  
 4  
 5  
 6  
 7  
 8  
 9  
10  
11  
12  
def main():
  draw(1)
  draw(2)
  draw(3)
  draw(4)
  draw(5)

def draw(x):
  print(x * '*') # this prints x stars in a row

if __name__ == "__main__":
    main()


Let's try it out Here

Example 2: Calculating if a small number is a prime 

 1  
 2  
 3  
 4  
 5  
 6  
 7  
 8  
 9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  
20  
21  
22  
23  
24  
25  
26  
27  
28  
29  
30  
31  
32  
33  
34  
35  
36  
37  
38  
def main():
  # what if num is 50? and 1147?
  num =  25

  # let's find out if x is prime
  result = is_prime(num)
  print ("Is {:d} a prime?: Result: {}".format(num, result))

# checks if the first 3 primes are factors of x
def is_prime(x):
  result = is_divisor(x,2)
  if result:
    print ("{:d} divides {:d}!".format(2, x))
    return not result
  result = is_divisor(x,3)
  if result:
    print ("{:d} divides {:d}!".format(3, x))  
    return not result
  result = is_divisor(x,4)
  if result:
    print ("{:d} divides {:d}!".format(4, x))  
    return not result  
  result = is_divisor(x,5)
  if result:
    print ("{:d} divides {:d}!".format(5, x))  
    return not result  
  return True  

# finds out if d is an exact divisor of x
def is_divisor(x, d):
  r = x%d
  if r == 0:
    return True
  else:
    return False  

if __name__ == "__main__":
    main()


Let's try it out Here

Activity 1 [2 minutes]:
Answer the following questions:

  1. Why are we checking only up to 5 when checking if num (25) is prime?
  2. Is there some unnecessary work done?
(Wait; then Click)
  1. Because in every pair of factors (exept an exact root), there is one large and one small one;
    we just need to check all the small ones up to and including the root.
  2. Yes, we technically don't need to check 4.




Can we do better?

The first thing to notice is that there are blocks of code that look very similar to one another.

very close!

OR

very close!

There are only small differences in the values used (directly or the ones inside variables).

we can take advantage of this if only there was some structure that would "perform the same block of code over and over again, until we're done with it".



Well, guess what?



The Loop

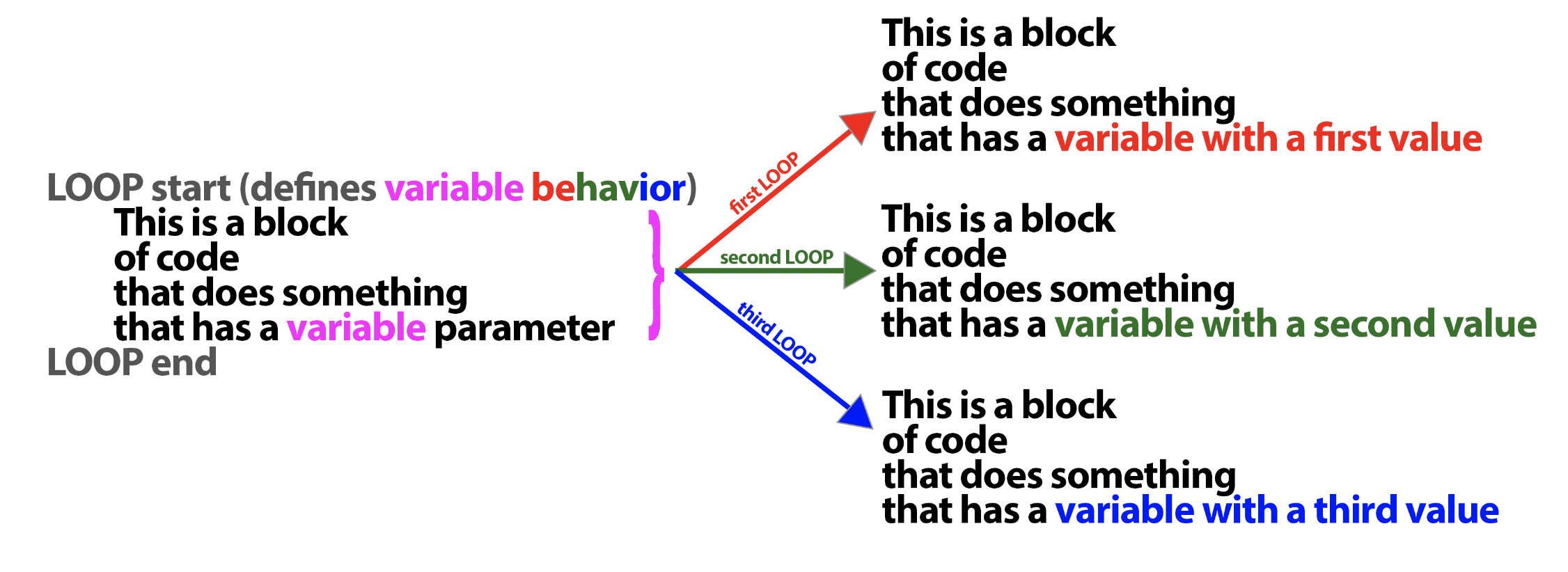
Before introducing the syntax, I'll show a diagram of what these structures (there are more than 1) do:

repeated

We can use a structure that "repeats the code" while also "updating some variable" in order to make each loop do the same work that the repeated code (previous image) was doing.

LOOP!!



The While Loop Syntax

while expression:  # Loop expression
    # Loop body: Sub-statements to execute
    # if the loop expression evaluates to True

# Statements to execute after the expression evaluates to Fals


Example 1: 

 1  
 2  
 3  
 4  
 5  
 6  
 7  
 8  
 9  
10  
11  
def main():
  draw(5)

def draw(lim):
    i = 1
    while i <= lim :
        print(i * '*') # this prints x stars in a row
        i+=1

if __name__ == "__main__":
    main()


Let's try it out Here



Example 2: 

 1  
 2  
 3  
 4  
 5  
 6  
 7  
 8  
 9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  
20  
21  
22  
23  
24  
25  
26  
27  
28  
29  
30  
31  
32  
# Calc if a number is a prime
def main():
  # what if num is 50? and 1147?
  num =  25

  # let's find out if x is prime
  result = is_prime(num)
  print ("Is {:d} a prime?: Result: {}".format(num, result))

# checks if there is a divisor in [2,x/2]
# not the most efficient, but ok
def is_prime(x):
  divisor = 2
  lim = x//2
  while divisor <= lim:
    result = is_divisor(x,divisor)
    if result:
      print ("{:d} divides {:d}!".format(divisor, x))
      return not result
    divisor+=1    
  return True  

# finds out if d is an exact divisor of x
def is_divisor(x, d):
  r = x%d
  if r == 0:
    return True
  else:
    return False  

if __name__ == "__main__":
    main()


Let's try it out Here



What could go wrong?

Activity 2 [2 minutes]:

What could go wrong with these structures?



The For Loop Syntax

Before we see the syntax for the for loop, we'll see one useful function: range.

The range function

range is a built-in function that accepts integer arguments (start , stop , step) and returns an immutable sequence of numbers.

Example: 

# r is the object range(0,10), 10 not included
r = range(10) 
print(r)
num_list = list(r)
print(num_list)
print (3 in r)
print(-1 in r)
print (10 in r)
# r2 is the object range(3,7), 7 not included
r2 = range(3, 7) 
num_list2 = list(r2)
print(num_list2)
# r3 is the object range(2,10), skipping to every 3rd; 10 not included
r3 = range(2, 10,3) 
num_list3 = list(r3)
print(num_list3)


the range is not like a string or a list, where the individual elements are stored independently.
It is an interval of integers.

It can be converted to a list (if so desired) but for our purposes, it is enough to use it directly as the container in the for loop parameters.

The For Loop Syntax

for variable in container:
    # Loop body: Sub-statements to execute
    # for each item in the container

# Statements to execute after the for loop is complete


Example 1: 
1  
2  
3  
4  
5  
6  
7  
8  
9  
def main():
  draw(5)

def draw(lim):
    for i in range(1,5) :
        print(i * '*') # this prints x stars in a row

if __name__ == "__main__":
    main()


Let's try it out Here

Activity 3 [2 minutes]:
Why do we use range(1,5) and not simply range(5)?




Example 2: 

 1  
 2  
 3  
 4  
 5  
 6  
 7  
 8  
 9  
10  
11  
12  
13  
14  
15  
16  
17  
18  
19  
20  
21  
22  
23  
24  
25  
26  
27  
28  
29  
30  
31  
# Calc if a number is a prime
def main():
  # what if num is 50? and 1147?
  num =  25

  # let's find out if x is prime
  result = is_prime(num)
  print ("Is {:d} a prime?: Result: {}".format(num, result))

# checks if there is a divisor in [2,x/2]
# not the most efficient, but ok
def is_prime(x):
  divisor = 2
  lim = x//2
  for divisor in range(2,lim):
    result = is_divisor(x,divisor)
    if result:
      print ("{:d} divides {:d}!".format(divisor, x))
      return not result   
  return True  

# finds out if d is an exact divisor of x
def is_divisor(x, d):
  r = x%d
  if r == 0:
    return True
  else:
    return False  

if __name__ == "__main__":
    main()


Let's try it out Here



Homework

[Due for everyone]
Remember: Homework 03 (Replit); due on 02/18 before 5 PM

[Optional] ZyBooks Sections 4.2, 4.4, 4.5, and 4.6